Ángulo Central de una Circunferencia

Un ángulo central se ubica en el centro de una circunferencia, y sus lados se extienden hasta cortar el perímetro en dos puntos, definiendo así un arco.

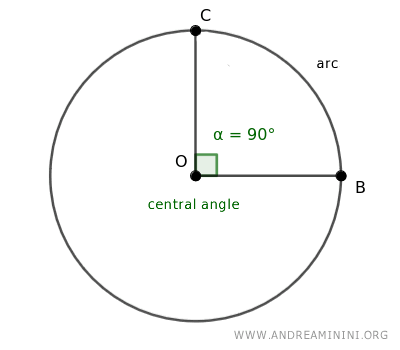
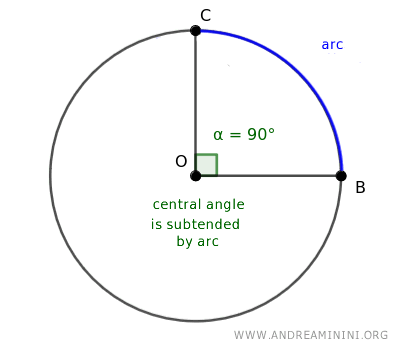
Se dice que este ángulo subtiende el arco, lo que significa que dicho arco abarca exactamente la abertura del ángulo.

En otras palabras, el ángulo central determina el arco, y el arco refleja la medida de ese ángulo.

Normalmente, al trazar dos semirrectas desde el centro de una circunferencia hacia su perímetro, se generan dos ángulos: uno cóncavo (mayor de 180°) y otro convexo (menor de 180°), o bien dos ángulos llanos de 180°.

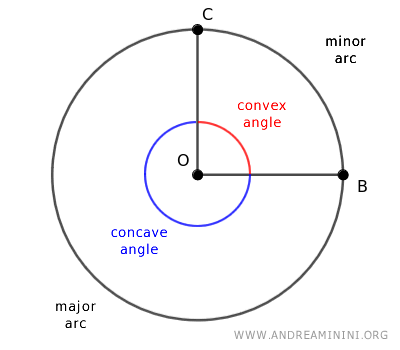
El ángulo convexo subtiende un arco menor, mientras que el cóncavo corresponde a un arco mayor.

Ángulo Central vs. Ángulo Inscrito: Una Distinción. Son conceptos geométricos diferentes. El vértice del ángulo central está situado en el centro de la circunferencia, mientras que el de un ángulo inscrito se encuentra sobre el perímetro.

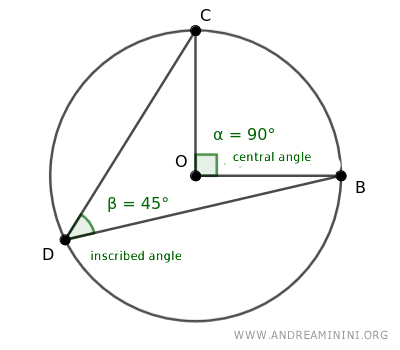
Un ángulo central (α) y un ángulo inscrito (β) se consideran correspondientes cuando abarcan el mismo arco.

Para un arco determinado AB, existe un único ángulo central (α) que lo subtiende, mientras que pueden existir infinitos ángulos inscritos (β, β',...) que corresponden al mismo arco.

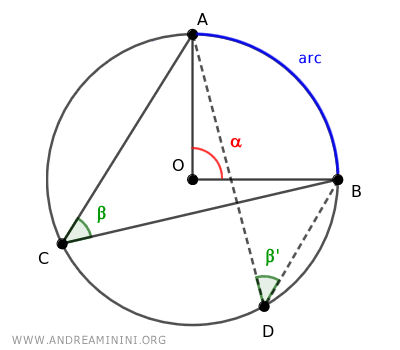
Todos los ángulos inscritos correspondientes que subtienden un mismo arco son congruentes (β≅β') y miden exactamente la mitad de su ángulo central correspondiente (β = α/2).

Aspectos Clave sobre los Ángulos Centrales

Algunos puntos esenciales y observaciones acerca de los ángulos centrales:

• El ángulo central mide el doble que cualquier ángulo inscrito correspondiente
  Por ejemplo, si el ángulo central mide α, cualquier ángulo inscrito β correspondiente al mismo arco tendrá una medida igual a la mitad (β = α/2).
  
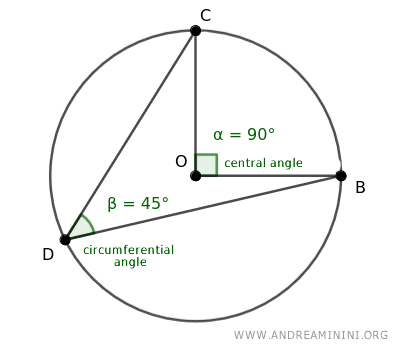
• Proporcionalidad entre el ángulo central y el arco subtenido
  La amplitud del ángulo central es directamente proporcional a la longitud del arco que subtiende, y viceversa. Así, un ángulo central de 360° abarca toda la circunferencia, mientras que uno de 180° abarca un semicírculo.
• Congruencia de ángulos
  En una circunferencia, dos ángulos centrales son congruentes (es decir, tienen la misma medida) únicamente si subtienden arcos de igual longitud. Además, cuanto mayor sea un arco, mayor será el ángulo central que lo subtiende.
• Suma de ángulos
  La suma de los ángulos centrales que subtienden dos arcos distintos y no superpuestos es igual al ángulo central que subtiende la unión de dichos arcos.
• La bisectriz de un ángulo central no solo divide el ángulo en dos partes iguales, sino que también biseca el arco correspondiente y es perpendicular a la cuerda asociada a ese arco.

Y así sucesivamente.