Teorema de las Tangentes a una Circunferencia desde un Punto Exterior

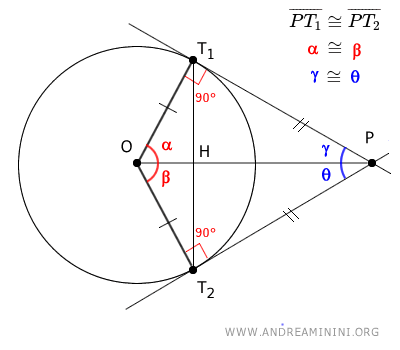
Consideremos una circunferencia y dos rectas tangentes que pasan por un punto P exterior a ella. Los segmentos que unen el punto P con los puntos de tangencia, T₁ y T₂, son congruentes, $ \overline{PT_1} \cong \overline{PT_2} $ (es decir, tienen la misma longitud).

 

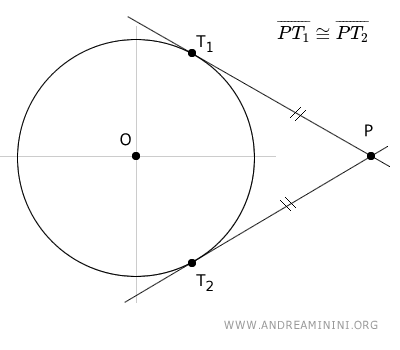
Además, conviene destacar tres propiedades fundamentales:

• El segmento OP, que conecta el centro O de la circunferencia con el punto exterior P, es el eje de simetría de la cuerda T₁T₂ y, por tanto, actúa como eje de simetría de los segmentos PT₁ y PT₂.
  
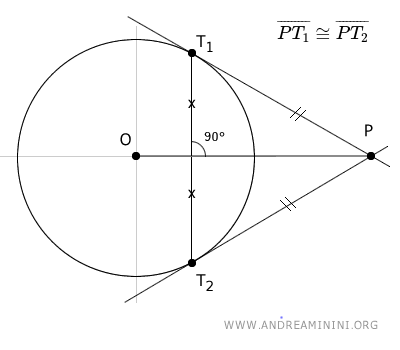
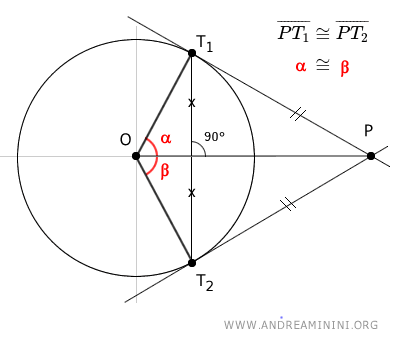
• El segmento OP biseca el ángulo (en rojo) formado por los radios de la circunferencia que unen el centro O con los puntos de tangencia T₁ y T₂.
  
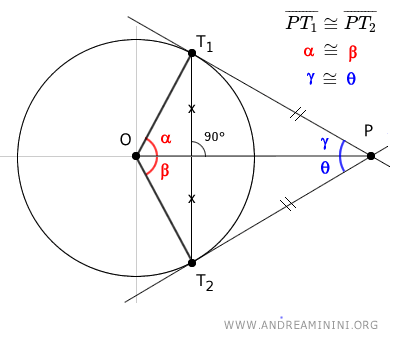
• El segmento OP también biseca el ángulo (en azul) formado por las dos rectas tangentes PT₁ y PT₂ en el punto P.
  

Demostración

Consideremos una circunferencia de radio OT₁ y dos rectas tangentes PT₁ y PT₂ que pasan por el punto exterior P.

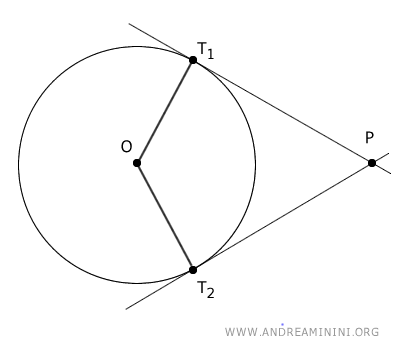
Se traza el segmento que une el centro O de la circunferencia con el punto exterior P.

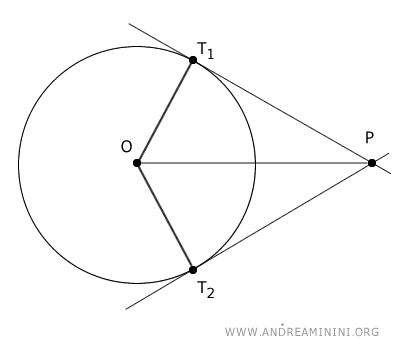
Los puntos de tangencia sobre la circunferencia son T₁ y T₂.

Los segmentos OT₁ y OT₂ son congruentes, pues ambos son radios de la circunferencia.

$$ \overline{OT_1} \cong \overline{OT_2} $$

Sabemos que los radios de una circunferencia siempre son perpendiculares a las rectas tangentes. Por ello, los radios OT₁ y OT₂ forman ángulos rectos de 90° con los segmentos PT₁ y PT₂, respectivamente.

$$ \overline{OT_1} \perp \overline{PT_1} $$

$$ \overline{OT_2} \perp \overline{PT_2} $$

Por tanto, los triángulos OPT₁ y OPT₂ son triángulos rectángulos.

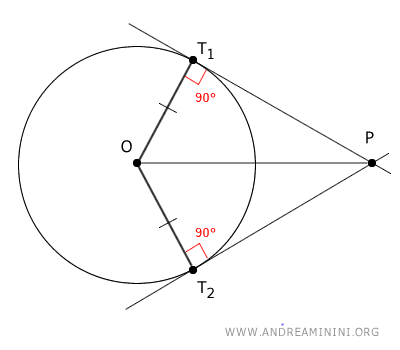
Estos dos triángulos rectángulos son congruentes según el teorema de congruencia de triángulos rectángulos, ya que comparten la hipotenusa OP y tienen un cateto congruente OT₁ = OT₂.

$$ OPT_1 \cong OPT_2 $$

Siendo congruentes, todos sus lados y ángulos son iguales, coincidiendo en orden.

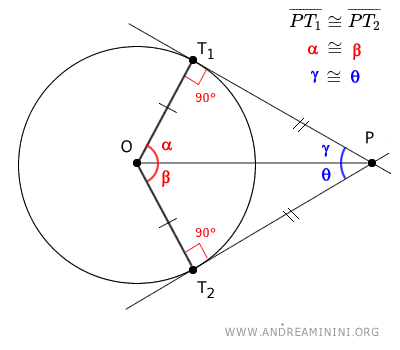
Esto prueba que los segmentos PT₁ y PT₂ son congruentes.

$$ \overline{PT_1} \cong \overline{PT_2} $$

Además, los ángulos α = β y γ = θ también son congruentes.

$$ \alpha \cong \beta $$ $$ \gamma \cong \theta $$

Por tanto, el segmento OP biseca tanto el ángulo central O formado por los radios como el ángulo entre las rectas tangentes en el punto P.

Finalmente, se traza la cuerda T₁T₂ entre los dos puntos de tangencia.

El triángulo OT₁T₂ es un triángulo isósceles, pues sus lados OT₁ y OT₂ son congruentes por ser radios de la circunferencia.

El segmento OH es bisectriz en el triángulo, ya que sabemos que los ángulos α y β son congruentes.

Dado que en un triángulo isósceles, la bisectriz coincide con la altura, la mediana y el eje de simetría, se deduce que:

• El segmento OH es perpendicular a la cuerda T₁T₂ porque OH actúa como altura del triángulo.
• El punto H es el punto medio de la cuerda T₁T₂ porque OH también es mediana.

Por tanto, el segmento OH constituye el eje de simetría del triángulo OT₁T₂.

Y dado que OH forma parte del segmento OP, queda demostrado que el segmento OP es el eje de la cuerda T₁T₂ que une los dos puntos de tangencia.

Y con esto, el teorema queda completamente demostrado.