Círculo
Un círculo es una figura geométrica bidimensional formada por todos los puntos de su circunferencia y por aquellos que se hallan en su interior.
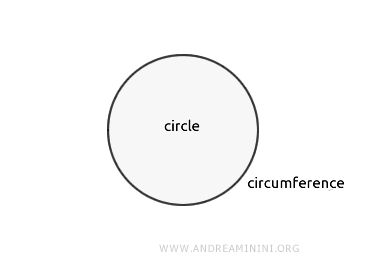
Otra forma de definir un círculo es como el conjunto de todos los puntos de un plano situados a una distancia igual o menor que su radio (r) respecto a un punto central O.
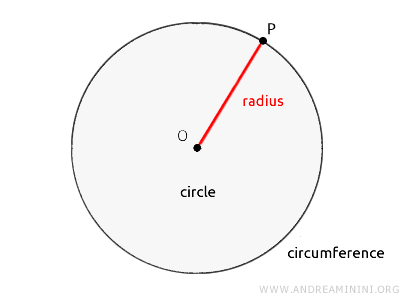
El radio es el segmento que une el centro del círculo (O) con cualquier punto de su contorno.
Desde tiempos remotos, los círculos han cautivado a la humanidad, despertando el interés de civilizaciones como la egipcia, la babilónica o la griega, que estudiaron sus propiedades y los aplicaron en ámbitos tan diversos como la arquitectura o la astronomía.
Conceptos Fundamentales del Círculo
La circunferencia constituye el perímetro del círculo.
La fórmula para calcular la longitud de la circunferencia, C, se obtiene multiplicando el diámetro (d) por la constante matemática π (pi).
$$ C = \pi \cdot d $$
Dado que el diámetro es simplemente el doble del radio (d = 2r), la fórmula también puede expresarse como C = 2πr, donde r es el radio del círculo.
$$ C = 2 \pi \cdot r $$
La constante π (pi) expresa la razón entre la circunferencia de un círculo y su diámetro, y su valor es aproximadamente 3,14. Esta relación es invariable, sin importar el tamaño del círculo, ya que siempre se mantiene la misma proporción entre la circunferencia y el diámetro.
Un arco es, en esencia, un segmento de la circunferencia del círculo.
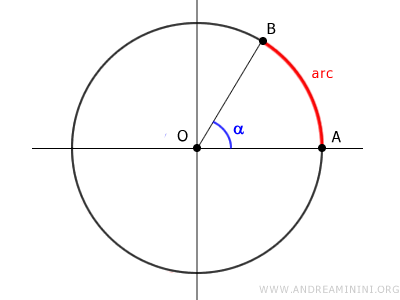
La longitud de un arco (L) está directamente vinculada al ángulo central (α) que abarca.
$$ L:C = \alpha : 360° $$
Esto significa que la longitud de un arco, en comparación con la circunferencia completa, guarda la misma proporción que su ángulo central respecto a los 360 grados del círculo completo.
Para hallar el área de un círculo, se multiplica π (aproximadamente 3,14) por el cuadrado del radio (r).
$$ A = \pi r^2 $$
El diámetro es un segmento recto que atraviesa el centro del círculo y conecta dos puntos de su contorno, midiendo exactamente el doble que el radio.
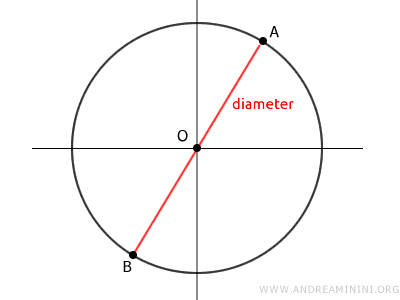
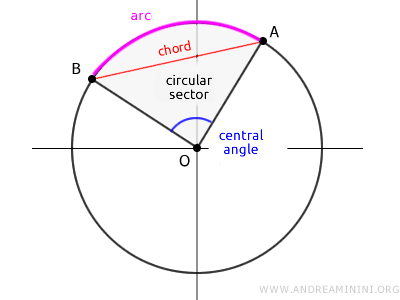
Una cuerda es un segmento cuyos extremos se encuentran sobre la circunferencia, pero a diferencia del diámetro, no necesariamente pasa por el centro.
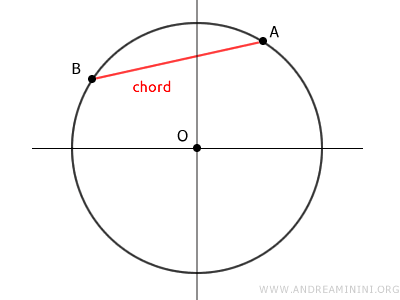
Cualquier cuerda divide el círculo en dos zonas, cada una llamada segmento circular o segmento de círculo, delimitado por un solo arco.
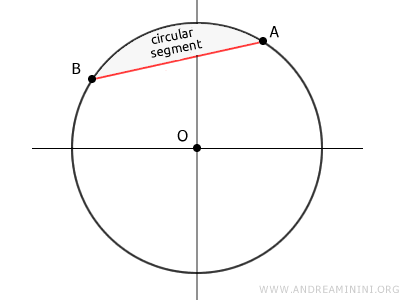
Si el segmento circular es menor que un semicírculo, su área se obtiene restando el área del triángulo OAB al área del sector circular correspondiente.
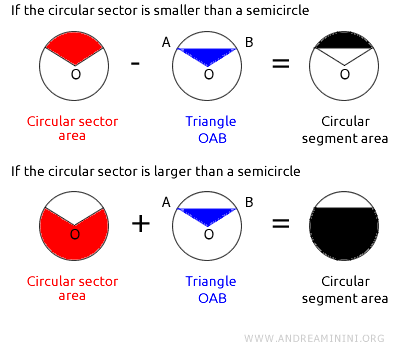
En cambio, si el segmento circular es mayor que un semicírculo, su área resulta de sumar el área del sector circular y la del triángulo OAB.
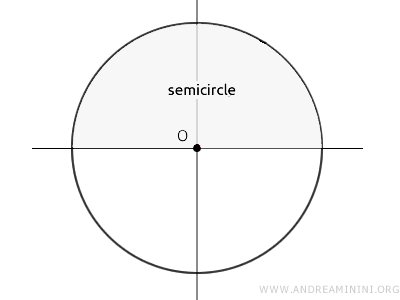
Por semicírculo entendemos la mitad de un círculo.
Un segmento circular delimitado por dos arcos, llamado segmento circular con dos bases, se encuentra entre dos cuerdas paralelas.
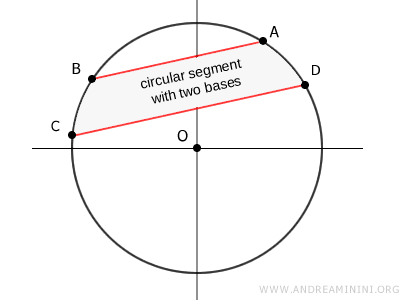
Para calcular su área, se resta la suma de las áreas de los dos segmentos simples generados por las cuerdas AB y CD al área total del círculo (A).
Un sector (o sector circular) es la porción del círculo con forma de cuña, delimitada por dos radios y el arco comprendido entre ellos.
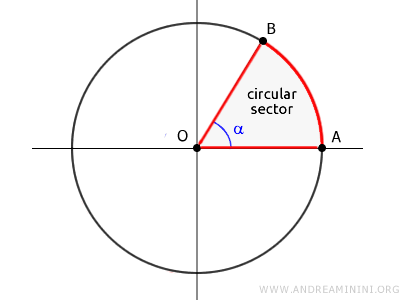
El área del sector es proporcional al tamaño de su ángulo central (α).
$$ A_s : A = \alpha : 360° $$
Esta fórmula indica que el área de un sector, como fracción del área total del círculo, equivale a la proporción de su ángulo central respecto a los 360 grados de un círculo completo.
La corona circular es la zona comprendida entre dos círculos concéntricos que comparten el mismo centro pero tienen radios distintos.
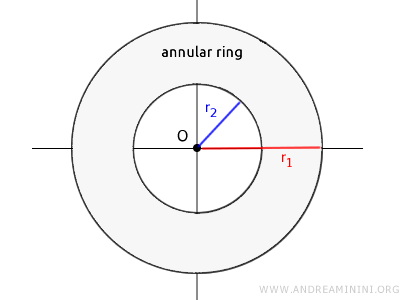
Su área se obtiene restando el área del círculo menor al área del círculo mayor.
$$ A_c = \pi \cdot r_1^2 - \pi \cdot r_2^2 $$
Fórmulas Clave del Círculo
Las fórmulas más importantes para calcular las dimensiones de un círculo son:
- Circunferencia
La longitud de la circunferencia (C) se calcula multiplicando el doble del radio (r) por π (3,14) $$ C = 2r \cdot \pi $$ Como el diámetro es el doble del radio, también puede expresarse como $$ C = d \cdot \pi $$ - Área
El área de un círculo se obtiene multiplicando el cuadrado del radio (r) por π (3,14) $$ A = r^2 \cdot \pi $$ - Longitud de un Arco
La longitud de un arco (L) es proporcional al ángulo central (α) que abarca $$ L:C = α:360° $$ Así, se calcula mediante la fórmula $$ L = \frac{ \alpha \cdot C }{360} $$ - Área de un Sector
El área de un sector As es proporcional al ángulo central (α) que delimita $$ A_s : A = α:360° $$ Por lo tanto, se calcula con la fórmula $$ A_s = \frac{ \alpha \cdot A }{360} $$ - Área de una Corona Circular
El área de la corona circular Ac se obtiene restando el área del círculo menor a la del mayor $$ A_c = \pi \cdot r_1^2 - \pi \cdot r_2^2 = \pi \cdot (r_1^2 - r_2^2) $$
Curiosidades sobre los Círculos
Algunos datos interesantes acerca de los círculos son:
- Los círculos son figuras convexas, lo que significa que cualquier segmento que una dos puntos dentro del círculo se encuentra completamente contenido en su interior.
Demostración. Una figura es convexa si todo segmento que conecta dos puntos de su interior permanece dentro de ella. Consideremos dos puntos A y B en el interior del círculo y el segmento AB que los une. Existen dos casos:
1] Si A y B están sobre el mismo diámetro, el segmento AB mide como máximo lo mismo que el diámetro, por lo que se halla por completo dentro del círculo.
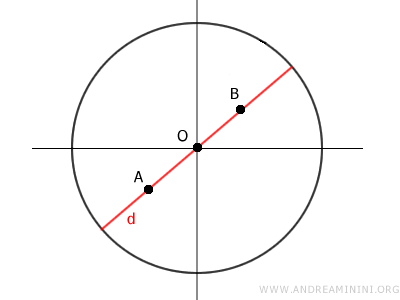
2] Si A y B no se sitúan sobre el mismo diámetro, se forma un triángulo OAB, siendo O el centro del círculo. Tomando cualquier punto C sobre AB, se puede demostrar que OC siempre es menor que OA o que OB, lo que prueba que el segmento entero se mantiene dentro del círculo.
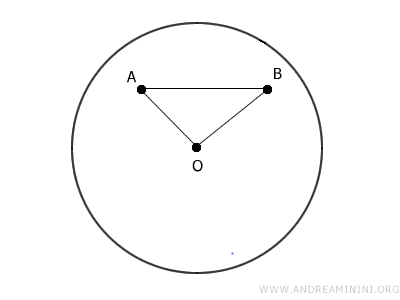
Esto demuestra que cualquier segmento comprendido en el círculo permanece en su interior, lo que confirma su carácter convexo. - Principios de Congruencia en los Círculos
En un círculo, si dos cuerdas, arcos, sectores, segmentos o ángulos centrales son congruentes, entonces todas las figuras correspondientes también lo son, reflejando una correspondencia perfecta dentro de la geometría del círculo.
Y así sucesivamente