Circunferencias secantes
Decimos que dos circunferencias son secantes cuando tienen exactamente dos puntos en común.
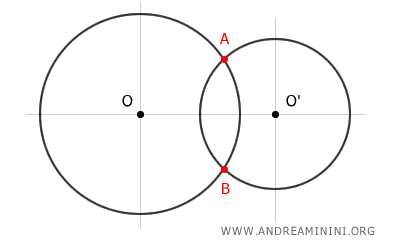
Desde el punto de vista geométrico, es imposible que dos circunferencias se corten en más de dos puntos, ya que tres puntos distintos determinan, de forma única, una sola circunferencia.
Por tanto, si dos circunferencias compartiesen tres puntos, en realidad serían la misma circunferencia.
Teorema de las circunferencias secantes
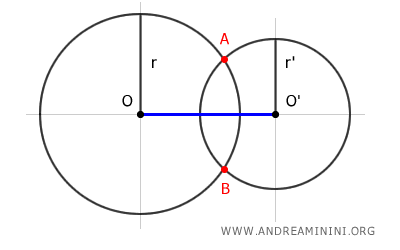
Para que dos circunferencias se corten, la distancia entre sus centros debe ser menor que la suma de sus radios y mayor que la diferencia de sus radios. $$ | r - r' | < OO' < r + r' $$
Demostración
La demostración consiste en trazar la recta OO' que une los centros de las dos circunferencias y prolongar los radios de ambas hasta uno de los puntos de intersección, que llamaremos punto A.
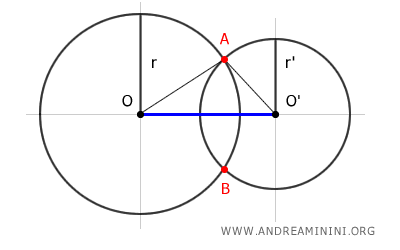
Esta construcción forma el triángulo OO'A.
Por el teorema de la desigualdad triangular, sabemos que la longitud de un lado de un triángulo es siempre menor que la suma y mayor que la diferencia de los otros dos lados.
Por tanto, la distancia OO' entre los centros debe ser menor que la suma de los radios (r + r') y mayor que su diferencia (r - r').
Cómo determinar los puntos de intersección
Para hallar los puntos de intersección de dos circunferencias secantes, recurrimos a la geometría analítica.
Consideremos dos circunferencias con centros en \((x_1, y_1)\) y \((x_2, y_2)\), y radios \(r_1\) y \(r_2\):
Sus ecuaciones son:
\[ (x - x_1)^2 + (y - y_1)^2 = r_1^2 \]
\[ (x - x_2)^2 + (y - y_2)^2 = r_2^2 \]
Para encontrar los puntos de intersección, se siguen estos pasos:
- Plantear un sistema con las ecuaciones de ambas circunferencias: \[ \begin{cases} x^2 + y^2 - 2x_1x - 2y_1y + x_1^2 + y_1^2 = r_1^2 \\ x^2 + y^2 - 2x_2x - 2y_2y + x_2^2 + y_2^2 = r_2^2 \end{cases} \]
- Restar una ecuación de la otra para eliminar los términos \(x^2\) y \(y^2\), obteniendo una ecuación lineal.
- Despejar una variable (por ejemplo \(y\)) en función de \(x\).
- Sustituir la expresión obtenida en una de las ecuaciones originales.
- Resolver la ecuación cuadrática resultante para \(x\) aplicando la fórmula general: \[ ax^2 + bx + c = 0 \] \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Con los valores de \(x\), sustituir de nuevo para hallar los correspondientes valores de \(y\).
Así se obtienen las coordenadas \((x, y)\) de los puntos de intersección de ambas circunferencias.
Ejemplo
Analicemos dos circunferencias secantes cuyas ecuaciones son:
$$ C_1 : \ x^2 + y^2 = 25 $$
$$ C_2 : \ (x - 4)^2 + (y - 3)^2 = 16 $$
La primera describe una circunferencia con centro en el origen O(0, 0) y radio \( r_1 = 5 \).
La segunda representa una circunferencia con centro en (4, 3) y radio \( r_2 = 4 \).
La distancia entre sus centros, OO', se calcula así:
$$ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
$$ d = \sqrt{(0 - 4)^2 + (0 - 3)^2} $$
$$ d = \sqrt{16 + 9} = \sqrt{25} = 5 $$
Según el teorema, dos circunferencias se cortan si la distancia entre sus centros es menor que la suma de sus radios y mayor que la diferencia de los mismos:
$$ | r_1 - r_2 | < d < r_1 + r_2 $$
$$ | 5 - 4 | < 5 < 5 + 4 $$
$$ 1 < 5 < 9 $$
Por tanto, estas circunferencias se cortan.
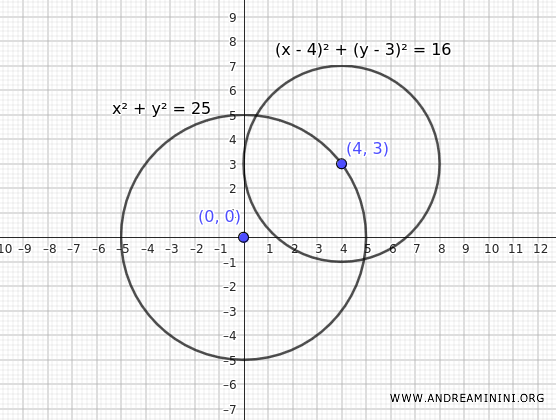
¿Cuáles son los puntos de intersección de estas circunferencias?
Primero, desarrollamos la segunda ecuación:
\[ (x - 4)^2 + (y - 3)^2 = 16 \]
\[ x^2 - 8x + 16 + y^2 - 6y + 9 = 16 \]
\[ x^2 + y^2 - 8x - 6y + 25 = 16 \]
\[ x^2 + y^2 - 8x - 6y + 9 = 0 \]
Planteamos el sistema:
\[ \begin{cases} x^2 + y^2 = 25 \\ x^2 + y^2 - 8x - 6y + 9 = 0 \end{cases} \]
Restamos la primera ecuación de la segunda:
\[ \begin{cases} x^2 + y^2 = 25 \\ (x^2 + y^2 - 8x - 6y + 9) - (x^2 + y^2) = 0 - 25 \end{cases} \]
\[ \begin{cases} x^2 + y^2 = 25 \\ -8x - 6y + 9 = -25 \end{cases} \]
\[ \begin{cases} x^2 + y^2 = 25 \\ -8x - 6y = -34 \end{cases} \]
Multiplicamos por -1 para simplificar:
\[ \begin{cases} x^2 + y^2 = 25 \\ 8x + 6y = 34 \end{cases} \]
\[ \begin{cases} x^2 + y^2 = 25 \\ 4x + 3y = 17 \end{cases} \]
Despejamos \( y \):
\[ \begin{cases} x^2 + y^2 = 25 \\ y = \frac{17 - 4x}{3} \end{cases} \]
Sustituimos en la primera ecuación:
\[ \begin{cases} x^2 + \left( \frac{17 - 4x}{3} \right)^2 = 25 \\ y = \frac{17 - 4x}{3} \end{cases} \]
\[ x^2 + \frac{(17 - 4x)^2}{9} = 25 \]
Multiplicamos por 9:
\[ 9x^2 + (17 - 4x)^2 = 225 \]
Desarrollamos y simplificamos:
\[ 9x^2 + 289 - 136x + 16x^2 = 225 \]
\[ 25x^2 - 136x + 64 = 0 \]
Resolvemos la ecuación cuadrática:
\[ x = \frac{136 \pm \sqrt{136^2 - 4 \cdot 25 \cdot 64}}{50} \]
\[ x = \frac{136 \pm \sqrt{18496 - 6400}}{50} \]
\[ x = \frac{136 \pm \sqrt{12096}}{50} \]
\[ x = \frac{136 \pm 110}{50} \]
Así, obtenemos:
\[ x = \frac{246}{50} = 4.92 \]
\[ x = \frac{26}{50} = 0.52 \]
Sustituimos en la ecuación de \( y \):
$$ y = \frac{17 - 4x}{3} $$
- Para \( x = 4.92 \): \[ y = \frac{17 - 4 \cdot 4.92}{3} = \frac{17 - 19.68}{3} = \frac{-2.68}{3} = -0.893 \]
- Para \( x = 0.52 \): \[ y = \frac{17 - 4 \cdot 0.52}{3} = \frac{17 - 2.08}{3} = \frac{14.92}{3} = 4.973 \]
Por tanto, los puntos de intersección son aproximadamente \((4.92, -0.893)\) y \((0.52, 4.973)\).
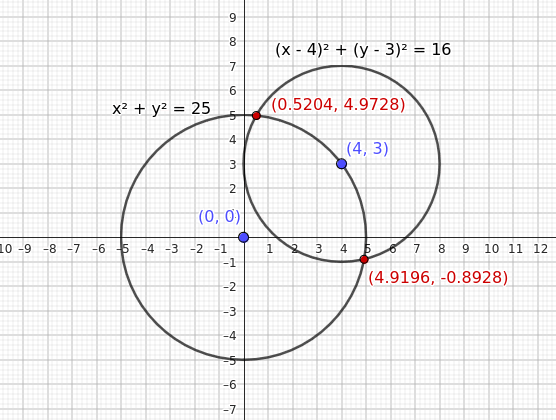
Estos son los puntos donde se intersectan las dos circunferencias secantes.
Aspectos clave sobre circunferencias secantes
Entre las propiedades más destacadas de las circunferencias secantes, encontramos:
- La cuerda AB, que une los puntos de intersección, es perpendicular a la recta OO' que une los centros de ambas circunferencias.
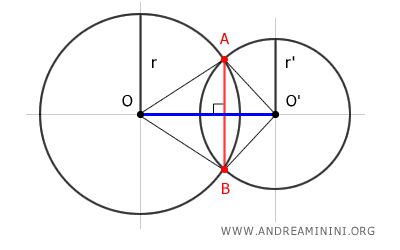
Motivo: Consideremos dos circunferencias secantes en los puntos A y B. Si unimos sus centros O y O' mediante la recta OO', y trazamos los segmentos OA, OB, O'A y O'B, notamos que OA y OB son iguales por ser radios de la primera circunferencia, y O'A y O'B también lo son, al ser radios de la segunda. $$ \overline{OA} \cong \overline{OB} $$ $$ \overline{O'A} \cong \overline{O'B} $$ Esto implica que A y B están a igual distancia de ambos centros, lo que demuestra que la cuerda AB es perpendicular a la recta OO'.