Pi
Pi es un número irracional que expresa la relación entre la longitud de la circunferencia (C) de cualquier círculo y su diámetro (d). Su valor aproximado es $$ \pi = \frac{C}{d} = 3.1415926535 $$
Como π (pi) es irracional, no puede representarse exactamente mediante una fracción y su desarrollo decimal es infinito y no periódico.
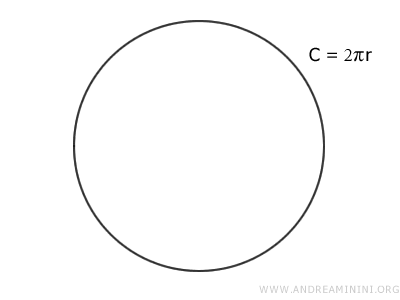
Se utiliza la letra griega π porque es la inicial de la palabra «perímetro». Gracias a este valor, se puede calcular la longitud de una circunferencia C=2πr, es decir, el perímetro del círculo.
$$ C = \pi \cdot d = \pi \cdot 2r $$
Donde r es el radio de la circunferencia, que siempre equivale a la mitad del diámetro, es decir, d=2r.
El matemático griego Arquímedes fue el primero en calcular el valor de pi con una precisión de dos cifras decimales, utilizando polígonos de 96 lados como referencia.
La Historia de Pi
Los orígenes del número 3,14, conocido universalmente como Pi (π), se remontan a las civilizaciones más antiguas de la humanidad, profundamente ligadas a la geometría clásica.
Muy pronto se descubrió que la proporción entre la longitud de la circunferencia y su diámetro es un valor constante.
En otras palabras, sin importar el tamaño del círculo, al dividir su perímetro entre el diámetro, siempre se obtiene un valor cercano a π, que ronda los 3,14.
Las primeras aproximaciones se deben a los babilonios y a los egipcios.
Los babilonios empleaban un valor aproximado de 3 1/8 (3,125) para π, mientras que en el Papiro Rhind aparece una estimación egipcia cercana a 3,16.
Estas primeras aproximaciones resultan asombrosamente precisas si consideramos los métodos rudimentarios de medición y cálculo de la época.
Sin embargo, fueron los antiguos griegos quienes perfeccionaron el cálculo, gracias a matemáticos como Arquímedes.
Arquímedes de Siracusa, quien vivió en el siglo III a. C., elevó el cálculo de π a un nivel extraordinario de precisión mediante un ingenioso método geométrico que hoy conocemos como el método de exhaución.
Utilizó polígonos regulares inscritos y circunscritos para aproximar la longitud de la circunferencia.
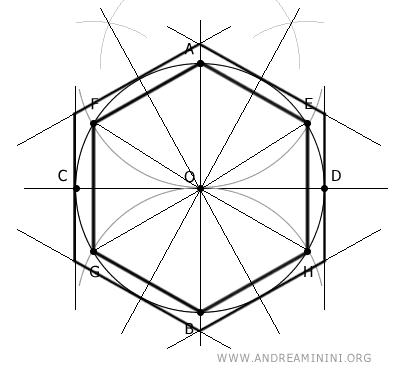
En concreto, empezó trabajando con hexágonos y fue duplicando sucesivamente el número de lados de los polígonos, ¡hasta alcanzar una figura de nada menos que 96 lados!
Gracias a este método, Arquímedes logró establecer que el valor de π se encontraba entre 3 1/7 (aproximadamente 3,1429) y 3 10/71 (aproximadamente 3,1408), una aproximación increíblemente precisa para aquella época.
Hoy en día conocemos esta constante matemática por la letra «pi» (π).
De hecho, esta denominación es mucho más reciente. Fue introducida en 1706 por el matemático galés William Jones y adoptada posteriormente, en el siglo XVIII, por el suizo Leonhard Euler.
Nota. Con la llegada de los ordenadores, se ha logrado calcular el número π con millones de cifras decimales de precisión. Es un desafío matemático que sigue vigente y que a menudo se utiliza para poner a prueba los límites del cálculo numérico por ordenador y de la teoría de números.
Cálculo de Pi
La búsqueda del valor de pi surge de la necesidad de calcular el perímetro de un círculo, es decir, determinar la longitud de su circunferencia.
La circunferencia de un círculo se expresa mediante la fórmula C=2πr
Para empezar, construyo un hexágono regular inscrito en la circunferencia.
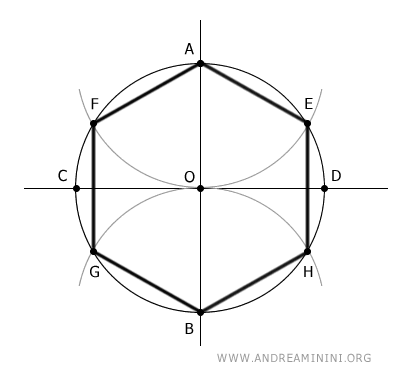
Nota. Para dibujar un hexágono inscrito, basta con trazar los ejes perpendiculares y dibujar dos arcos con el mismo radio que la circunferencia.
La distancia entre el centro de la circunferencia (O) y cualquiera de los vértices del hexágono inscrito es igual al radio.
$$ \overline{OA} = \overline{OB} = ... = r $$
Como el hexágono tiene seis lados y la suma de los ángulos alrededor del centro de un círculo es 360°, el ángulo central ∠AOE que abarca un sexto de la circunferencia mide 360°/6=60°.
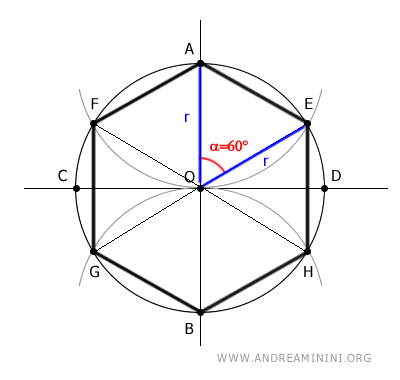
El triángulo OAE es un triángulo isósceles porque tiene dos lados congruentes, OA≅OE, ya que ambos miden el radio de la circunferencia: OA=r y OE=r.
En un triángulo isósceles, los ángulos de la base son iguales. Por eso, puedo deducir que los ángulos β≅γ del triángulo OAE son congruentes.
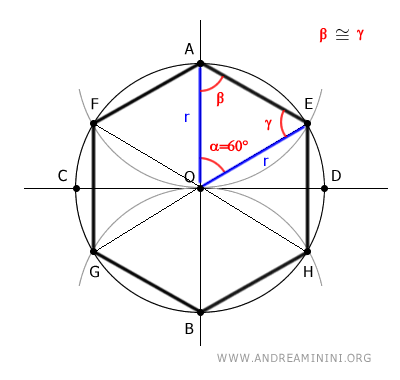
Dado que uno de los ángulos del triángulo OAE mide 60° y la suma de los ángulos internos de un triángulo siempre es 180°, concluyo que la suma de los ángulos restantes es 120°.
$$ 180° - \alpha = \beta + \gamma $$
$$ 180° - 60° = \beta + \gamma $$
$$ 120° = \beta + \gamma $$
Como β y γ son congruentes, cada uno mide 60°.
$$ \beta = \gamma = 60° $$
Así, el triángulo OAE tiene sus tres ángulos congruentes β≅γ≅α≅60°.
Por lo tanto, el triángulo OAE es un triángulo equilátero, lo que implica que sus lados también son iguales.
$$ \overline{OA} \cong \overline{OE} \cong \overline{AE} $$
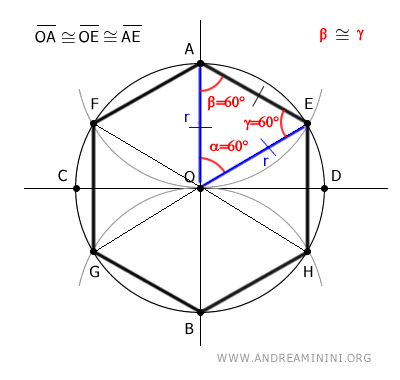
Como OA=OE=r, deduzco que el lado del hexágono AE=r es igualmente igual al radio de la circunferencia.
$$ \overline{AE} = r $$
Por tanto, en un hexágono regular inscrito en una circunferencia, el perímetro (P) del hexágono es seis veces el radio de la circunferencia.
$$ P = 6r $$
Al estar inscrito, su perímetro es menor que el de la circunferencia.
$$ 6 r < 2 \pi r $$
Divido ambos lados de la desigualdad entre dos:
$$ 3 r < \pi r $$
Y después divido entre r en ambos lados:
$$ 3 < \pi $$
Así, concluyo que el valor de pi es mayor que 3.
Ahora construyo un hexágono regular circunscrito alrededor de la circunferencia.
Para ello, trazo rectas que pasan por el centro y los puntos medios de los seis triángulos equiláteros que forman el hexágono inscrito.
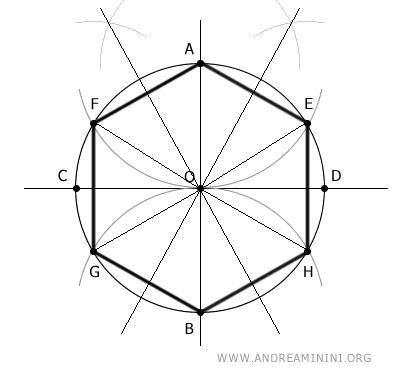
Después dibujo rectas tangentes a la circunferencia que cortan esas rectas en los puntos medios.
Para conseguirlo, basta con trazar líneas perpendiculares en dichos puntos medios.
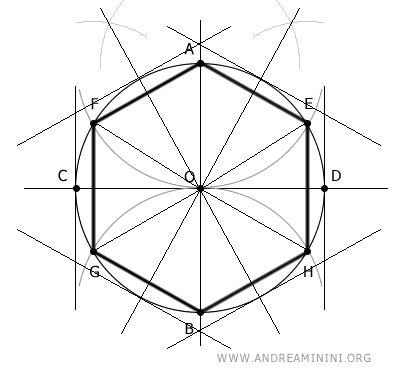
El resultado es un hexágono circunscrito.
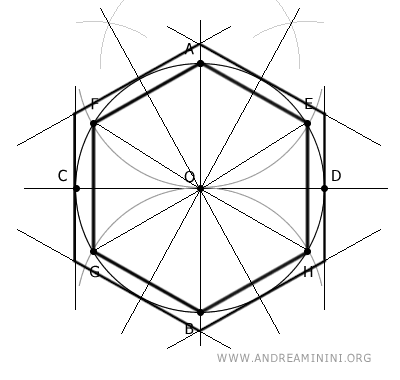
Para seguir el análisis con mayor claridad, muestro el dibujo solo con el hexágono circunscrito.
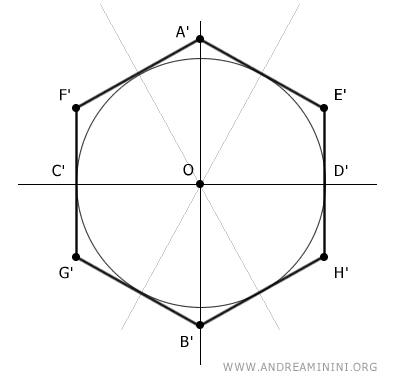
Trazo segmentos desde el centro hasta los vértices del hexágono A', B', E', F', G' y H'.
De este modo, divido el hexágono en seis triángulos congruentes.
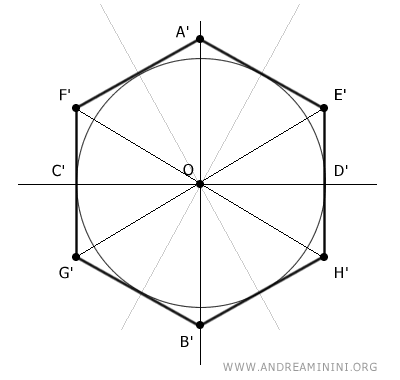
Me centro en el triángulo OE'H'.
Al igual que antes, el hexágono tiene seis lados y la suma de los ángulos centrales de una circunferencia es 360°, así que el ángulo central ∠E'OH' que corresponde a un sexto de la circunferencia mide 360°/6=60°.
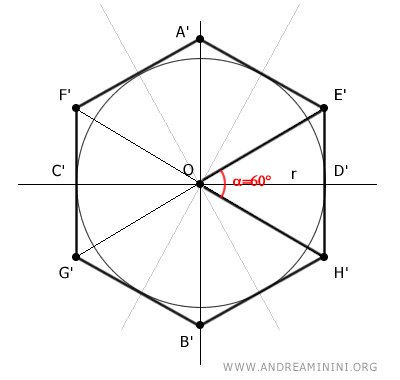
En este caso, el radio de la circunferencia coincide con el segmento OD', que es la altura del triángulo OE'H'.
El triángulo OE'H' está formado por dos triángulos rectángulos OE'D' y OH'D', cuyos ángulos internos miden 30°, 60° y 90°.
Por tanto, puedo calcular las longitudes de los catetos E'D' y H'D' usando la fórmula correspondiente a un triángulo rectángulo con ángulos de 30° y 60°.
$$ \overline{E'D'} = \frac{ \overline{OD'} \sqrt{3} }{3} $$
$$ \overline{H'D'} = \frac{ \overline{OD'} \sqrt{3} }{3} $$
Así, como el lado E'H'=E'D'+H'D', obtengo:
$$ \overline{E'H'} = 2 \cdot \frac{ \overline{OD'} \sqrt{3} }{3} $$
El segmento OD' es el radio de la circunferencia (r).
$$ \overline{E'H'} = 2 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
Una vez hallada la longitud del lado del hexágono en función del radio, calculo su perímetro.
El perímetro P del hexágono regular es seis veces la longitud del lado E'H'.
$$ P = 6 \cdot \overline{E'H'} $$
$$ P = 6 \cdot 2 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
$$ P = 12 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
$$ P = 4 \cdot r \cdot \sqrt{3} $$
Al ser un hexágono circunscrito, su perímetro es mayor que la longitud de la circunferencia C=2πr.
$$ P > C $$
$$ 4 \cdot r \cdot \sqrt{3} > 2 \pi \cdot r $$
Divido ambos lados de la desigualdad entre r:
$$ 4 \cdot \sqrt{3} > 2 \pi $$
Y despejo pi dividiendo ambos lados entre 2:
$$ 2 \cdot \sqrt{3} > \pi $$
El producto 2√3 es aproximadamente 3,46.
$$ 3.46 > \pi $$
Por tanto, el valor de pi es menor que 3,46.
En conclusión, gracias a los perímetros de los hexágonos inscrito y circunscrito, podemos afirmar que el valor de pi es mayor que 3 y menor que 3,46.
Nota. Esto pone de manifiesto que la longitud de la circunferencia constituye el límite entre la familia de perímetros de polígonos regulares inscritos y la de polígonos regulares circunscritos a una circunferencia.
Si se repite este procedimiento con polígonos de mayor número de lados, la aproximación del valor de pi se vuelve cada vez más precisa.
Conviene recordar que Arquímedes consiguió obtener las dos primeras cifras decimales del valor de pi empleando un polígono de 96 lados.
Curiosidades
Algunas reflexiones y datos interesantes sobre Pi.
- ¿Cómo memorizar Pi?
La mayoría recuerda Pi como 3,14, pero memorizar las cifras que siguen suele ser todo un reto. Una técnica habitual para recordarlas es recurrir a reglas mnemotécnicas. Por ejemplo, se puede crear una frase o un verso en el que el número de letras de cada palabra represente un dígito de Pi. Un ejemplo en inglés sería: "May I have a large container of coffee, cream, and sugar?"

Y así sucesivamente.