Arco de Circunferencia

Un arco de circunferencia es un segmento de la circunferencia delimitado por dos puntos, A y B.

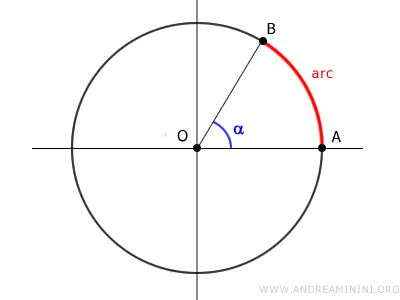
A estos puntos A y B se les conoce como extremos del arco.

Dicho de manera sencilla, un arco representa la distancia curva entre dos puntos distintos situados sobre la circunferencia.

Se diferencia así del segmento, que mide la distancia en línea recta entre esos mismos puntos.

Nota: Cuando se eligen dos puntos distintos A y B sobre la circunferencia, esta queda dividida en dos arcos complementarios. Para evitar ambigüedades, suele añadirse un tercer punto, C, que permite precisar a cuál de los dos arcos nos referimos. Por convención, si solo se mencionan A y B, se entiende que hablamos del arco que une A con B en sentido antihorario.

Cálculo de la Longitud del Arco

La longitud (L) de un arco se calcula multiplicando el ángulo central α (expresado en radianes) por el radio (r) de la circunferencia. $$ L = r \cdot \alpha_{rad} $$ Si el ángulo está dado en grados, la longitud del arco se obtiene mediante la fórmula: $$ L = r \cdot \frac{ \pi \cdot \alpha_{degrees} }{180} $$

Cuando el ángulo está en grados, es necesario convertirlo previamente a radianes:

$$ \alpha_{rad} = \frac{ \pi \cdot \alpha_{degrees} }{180} $$

Después, se sustituye α_rad en la fórmula de la longitud del arco:

$$ L = r \cdot \alpha_{rad} $$

Así, la fórmula final para calcular la longitud del arco queda:

$$ L = r \cdot \frac{ \pi \cdot \alpha_{degrees} }{180} $$

Un arco se llama arco completo cuando recorre toda la circunferencia, teniendo entonces una longitud de 2πr, siendo r el radio. $$ L = 2 \pi r $$

Nota: Esta fórmula refleja la proporcionalidad entre la longitud del arco y la longitud total de la circunferencia, en función del ángulo subtendido y de la vuelta completa de 360 grados. $$ 2 \pi : \alpha = 2 \pi r : L $$ Aquí, 2π representa la vuelta completa en radianes, α es el ángulo subtendido en radianes, 2πr es la longitud de la circunferencia, y L la longitud del arco. Reordenando la proporción: $$ 2 \pi : \alpha = 2 \pi r : L $$ Y expresándola como fracciones: $$ \frac{2 \pi }{ \alpha } = \frac{2 \pi r }{L } $$ Dividiendo ambos lados entre 2π se obtiene: $$ \frac{1 }{ \alpha } = \frac{ r }{L } $$ Multiplicando por L: $$ \frac{L }{ \alpha } = r $$ Y finalmente, multiplicando por α se concluye: $$ L = r \cdot \alpha $$ Así se deduce la fórmula para calcular la longitud de un arco en función del ángulo central.

Ejemplo

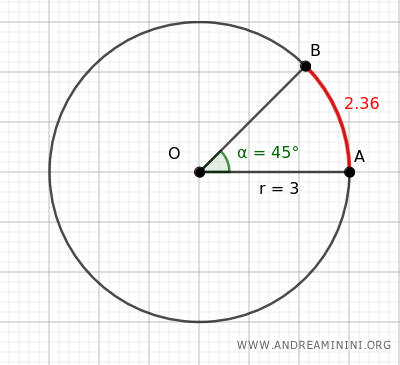
Consideremos una circunferencia de radio r=3.

Un ángulo central de 45° define un arco comprendido entre los puntos A y B de la circunferencia.

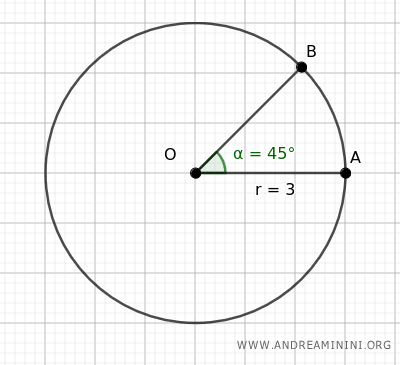
Sabemos que 45° equivale a π/4 radianes.

$$ \alpha = \frac{ \pi \cdot 45° }{180} = \frac{ \pi }{ 4 } $$

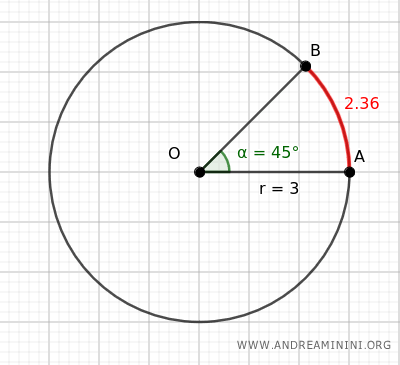
Por tanto, la longitud del arco L que va de A a B, en sentido antihorario, es:

$$ L = \alpha \cdot r = \frac{ \pi }{4} \cdot 3 \approx 2.36 $$

Así, la longitud del arco correspondiente a un ángulo central de 45° es aproximadamente 2.36.

Más Observaciones

Algunas consideraciones adicionales sobre los arcos de circunferencia:

Arcos iguales corresponden a ángulos centrales iguales y a ángulos iguales en la circunferencia.

• Proporcionalidad
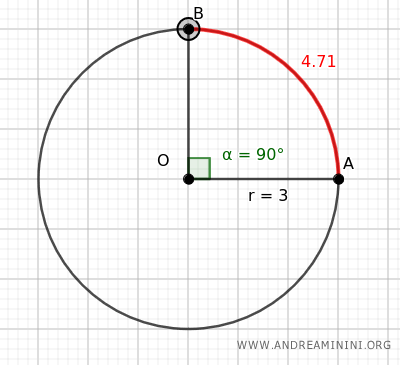
  La longitud de un arco es directamente proporcional al radio de la circunferencia. Por ejemplo, si se duplica el radio, la longitud del arco también se duplica.

  Nota: Por ejemplo, en una circunferencia de radio r=3 y un ángulo central de 45° (π/4 radianes), la longitud del arco es aproximadamente 2.356, que aquí redondeamos a 2.36. $$ L = \alpha \cdot r = \frac{ \pi }{4} \cdot 3 \approx 2.356 $$
  
  Si duplicamos el ángulo central a 90° (π/2 radianes), la longitud del arco se aproxima a 4.71, es decir, el doble de 2.356. $$ L = \alpha \cdot r = \frac{ \pi }{2} \cdot 3 \approx 4.71 $$
  

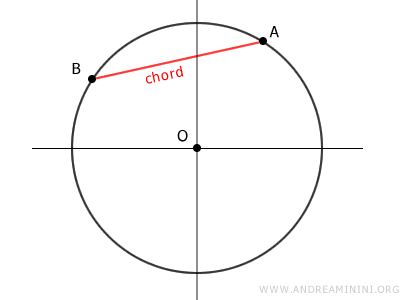
• Cuerda
  El segmento recto que une los extremos de un arco, A y B, se denomina cuerda. Cada arco se asocia a una cuerda determinada.
  
• Sector Circular
  La región delimitada por un arco y los dos radios que unen sus extremos con el centro de la circunferencia se denomina sector circular.
  

  

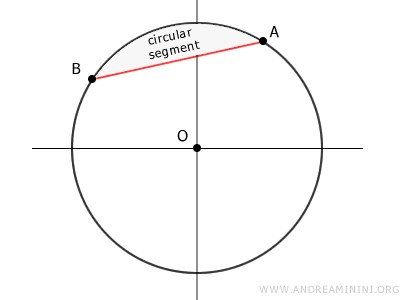
• Segmento Circular
  El área comprendida entre un arco y su correspondiente cuerda recibe el nombre de segmento circular.
  

  

Y así sucesivamente.