Polígonos Inscritos en Circunferencias
Se denomina polígono inscrito a aquel cuyos vértices se encuentran todos situados sobre la circunferencia de un círculo.
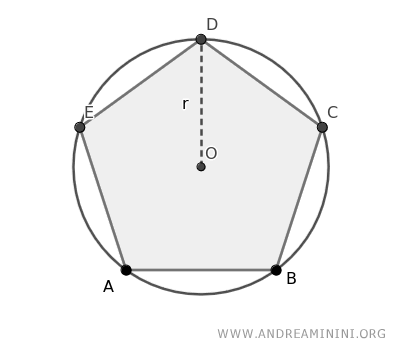
Esta relación también se puede expresar diciendo que la circunferencia circunscribe al polígono o que la circunferencia está circunscrita alrededor del polígono. En esencia, todas estas expresiones describen el mismo concepto.
Aunque las longitudes de los lados de un polígono inscrito pueden ser distintas, lo esencial es que todos sus vértices reposen exactamente sobre la circunferencia.
El centro de esta circunferencia circunscrita se denomina circuncentro.
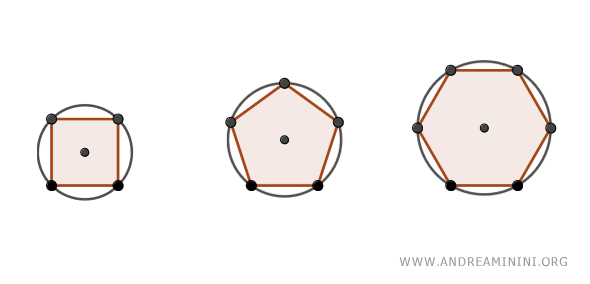
No todos los polígonos pueden inscribirse en una circunferencia. Por ejemplo, cualquier triángulo puede inscribirse siempre en un círculo, mientras que solo ciertos cuadriláteros poseen esa propiedad. En términos generales, todos los polígonos regulares - como pentágonos, hexágonos, etc. - pueden inscribirse en una circunferencia.
Un cuadrilátero inscrito en una circunferencia cumple siempre que sus ángulos opuestos suman 180° (α + β = 180°).
Teorema del Polígono Inscrito
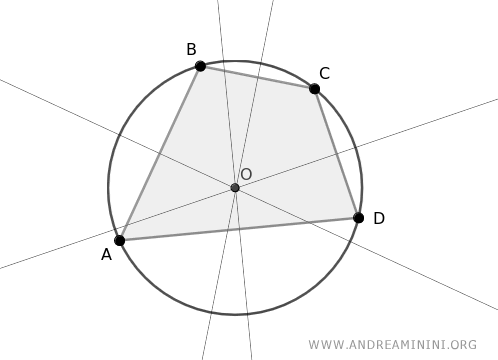
Una condición necesaria y suficiente para que un polígono sea inscrito en una circunferencia es que las mediatrices perpendiculares de sus lados concurran en un único punto, llamado circuncentro.
Si estas mediatrices no se intersectan en un único punto, el polígono no puede inscribirse en una circunferencia.
La recíproca también es cierta: si un polígono está inscrito en una circunferencia, entonces las mediatrices de sus lados se cortan en el centro de dicha circunferencia.
Ese punto de intersección único, el circuncentro, es una característica común a todos los triángulos, a todos los polígonos regulares y a ciertos polígonos irregulares que pueden inscribirse en una circunferencia.
Aplicación Práctica
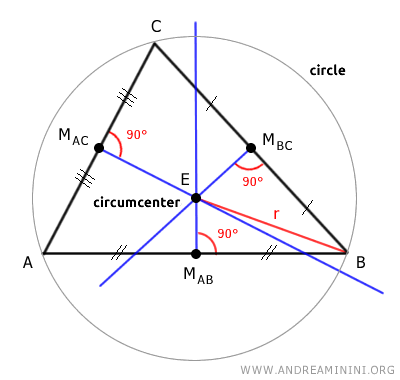
Consideremos, por ejemplo, un triángulo: sus mediatrices se intersectan siempre en un único punto denominado circuncentro del triángulo.
Si trazamos una circunferencia con centro en el circuncentro (E) y radio (r) adecuado, dicha circunferencia pasará exactamente por los tres vértices del triángulo.
Demostración
Consideremos un polígono cuyas mediatrices perpendiculares de los lados concurren en un punto O.
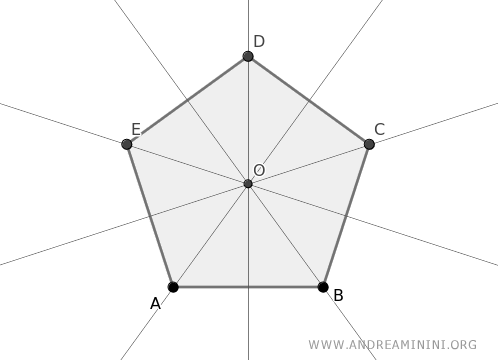
Aquí, la “mediatriz” de un lado es la recta perpendicular que pasa por el punto medio de ese lado y forma un ángulo recto (90°).
Queremos demostrar que un polígono con esta propiedad puede inscribirse en una circunferencia.
Por definición, una mediatriz es el lugar geométrico de los puntos equidistantes de los extremos de un segmento.
Por tanto, cualquier punto sobre una mediatriz está a igual distancia de los dos extremos del lado correspondiente del polígono.
Por ejemplo, el punto P, situado sobre la mediatriz del lado AB, está equidistante de los vértices A y B.
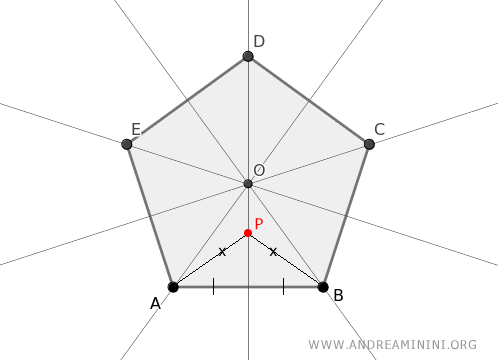
Esto implica que el punto de intersección O, donde confluyen todas las mediatrices, está equidistante de todos los vértices del polígono.
En otras palabras, la distancia d entre el punto O y cualquier vértice del polígono es constante.
$$ d = \overline{OA} = \overline{OB} = \overline{OC} = \overline{OD} = \overline{OE} $$
En consecuencia, se puede trazar una circunferencia con centro en O (circuncentro) y radio d, que pase por todos los vértices del polígono y, por tanto, circunscriba al polígono.
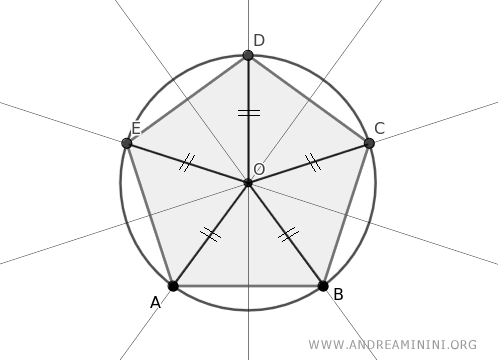
Así queda demostrado que el polígono está inscrito en una circunferencia.
Y así sucesivamente.