Polígonos equidescomponibles

Se denominan polígonos equidescomponibles o polígonos equicomponibles a aquellos polígonos que pueden descomponerse en un conjunto de polígonos más pequeños y congruentes.

En otras palabras, dos polígonos son equidescomponibles si es posible dividirlos en un número finito de partes (polígonos más pequeños), de manera que cada parte de un polígono sea congruente con una parte del otro, y viceversa.

Esto significa que es posible reorganizar las partes de un polígono para obtener el otro.

Por ejemplo, si dispongo de dos polígonos (Figura 1 y Figura 2) y puedo descomponer el primero en partes que, reordenadas, reproduzcan el segundo polígono - y recíprocamente - , entonces son polígonos equidescomponibles.

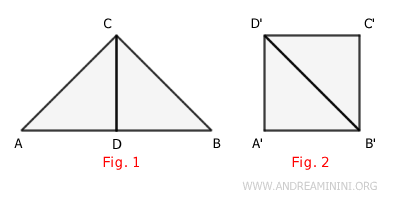
Nota: Este concepto guarda estrecha relación con el principio de Cavalieri, que establece que si dos sólidos en el espacio tridimensional son dispuestos de manera que todo plano paralelo a un plano fijo los intersecta en secciones de igual área, entonces dichos sólidos poseen el mismo volumen.

Un ejemplo práctico

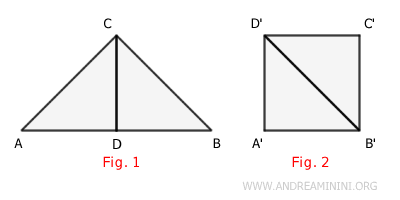
Consideremos dos polígonos: Figura 1 y Figura 2.

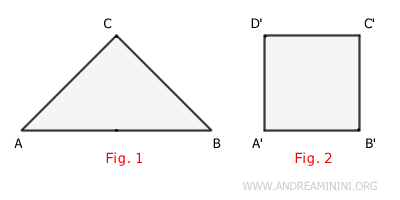
Descompongo el polígono de la Figura 1 en dos partes, cada una de las cuales es un polígono más pequeño (ACD y BCD).

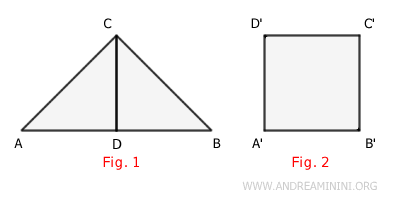
La suma de las áreas de los polígonos componentes es igual al área del polígono original A.

$$ Área(ABC) = Área(ACD) + Área(BCD) $$

A continuación, reorganizo estas dos partes de manera que, sin solaparse, cubran por completo la superficie del polígono B.

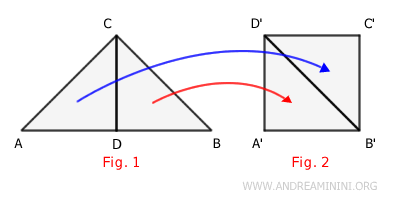
De ello se deduce que los polígonos A y B pueden descomponerse en los mismos polígonos congruentes y, por tanto, poseen la misma área (áreas equivalentes), es decir, ocupan la misma extensión.

$$ ACD \cong B'C'D' $$ $$ BCD \cong A'B'D' $$

En esencia, ambos se componen de la misma partición de polígonos.

Al tener la misma extensión, ambos presentan la misma área total, que corresponde a la suma de las áreas de los polígonos que los constituyen.

En tal caso, se denominan equidescomponibles.

Observaciones

Algunas consideraciones adicionales sobre los polígonos equidescomponibles:

• Dos polígonos son equidescomponibles incluso cuando resultan de la diferencia de polígonos congruentes
  Se aplican los mismos principios que en la suma de polígonos congruentes.
• Dos polígonos equidescomponibles tienen la misma área, es decir, son superficies equivalentes
  Por este motivo, también se les denomina polígonos equivalentes.
• La equidescomponibilidad es una relación de equivalencia
  Por lo tanto, se verifican las mismas propiedades matemáticas que caracterizan a cualquier relación de equivalencia. Las superficies de igual área pertenecen a la misma clase de equivalencia.
• Dos polígonos equidescomponibles son polígonos equivalentes
  Cuando dos polígonos están formados por las mismas partes, son equivalentes porque comparten la misma área.
• Teorema de Dehn
  Dos figuras equidescomponibles son también geométricamente equivalentes, aunque la recíproca no siempre es válida.

  Ejemplo: En el plano, dos polígonos equivalentes tienen la misma área y se componen de las mismas superficies equivalentes, por lo que siempre resultan equidescomponibles. En cambio, en el espacio tridimensional, dos poliedros con el mismo volumen no son necesariamente equidescomponibles.

• El concepto de equidescomponibilidad en la historia de la geometría y las matemáticas
  La noción de equidescomponibilidad ha tenido un papel destacado en la teoría de la medida, en particular en el estudio de la equivalencia de figuras geométricas en términos de área o volumen, y en la comprensión y demostración de las propiedades de dichas figuras.

  Ejemplo: Un caso célebre es el problema griego del cuadrado, que plantea la posibilidad de dividir un cuadrado en piezas que, reordenadas, permitan formar un círculo de igual área. Esta cuestión impulsó el desarrollo de la teoría de la medida y del cálculo integral moderno a lo largo de los siglos.

Y así sucesivamente.