Área de un polígono regular
El área de un polígono regular se calcula multiplicando el semiperímetro (p) por el apotema (a): $$ A = p \cdot a $$ donde el apotema es la distancia del centro del polígono a uno de sus lados, y el semiperímetro es la mitad del perímetro (2p = P, por tanto p = P/2).
Explicación
Este razonamiento se basa en dividir un polígono regular en varios triángulos congruentes, cada uno con un vértice en el centro y como base uno de los lados del polígono.
Por ejemplo, un hexágono puede dividirse en 6 triángulos congruentes.
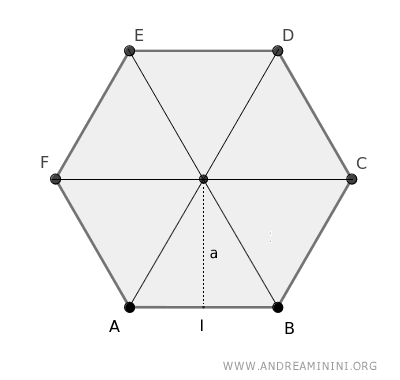
El área de cada triángulo se calcula con la fórmula clásica: base (l) por altura (h), dividido por dos:
$$ \frac{l \cdot h}{2} $$
En los polígonos regulares, la altura de estos triángulos es precisamente el apotema (a), es decir, la distancia desde el centro hasta un lado.
Por tanto, el área de un triángulo es:
$$ \frac{l \cdot a}{2} $$
Multiplicando por el número de lados (n), obtenemos el área total del polígono:
$$ A = n \cdot \frac{l \cdot a}{2} $$
Por ejemplo, para un hexágono: $$ A = 6 \cdot \frac{l \cdot a}{2} $$
Como el perímetro del polígono es $$ P = n \cdot l $$, podemos expresar la fórmula así:
$$ A = \frac{P \cdot a}{2} $$
Y como el semiperímetro es $$ p = \frac{P}{2} $$, la fórmula se simplifica aún más:
$$ A = p \cdot a $$
En resumen: el área de un polígono regular es igual al producto de su semiperímetro por su apotema.
Ejemplo práctico
Supongamos un hexágono regular con lado l = 6 y apotema a = 5.2.
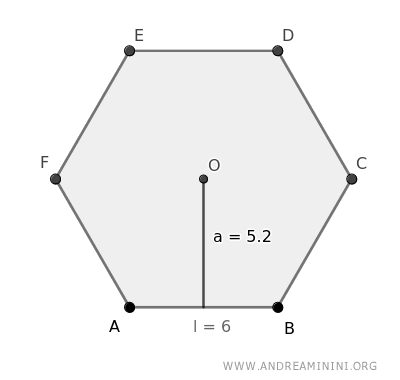
Primero calculamos el perímetro (P):
$$ P = 6 \cdot 6 = 36 $$
Después, el semiperímetro (p):
$$ p = \frac{P}{2} = \frac{36}{2} = 18 $$
Por último, el área:
$$ A = p \cdot a = 18 \cdot 5.2 = 93.6 $$
Por tanto, el área del hexágono es 93.6.
Nota: También puede calcularse el área de uno de los triángulos y multiplicar por 6: $$ A_t = \frac{l \cdot h}{2} = \frac{6 \cdot 5.2}{2} = \frac{31.2}{2} = 15.6 $$ $$ A = A_t \cdot 6 = 15.6 \cdot 6 = 93.6 $$
Esta fórmula es válida para cualquier polígono regular.
Sea un pentágono, un octógono o un decágono, el procedimiento es el mismo.
Ejemplo 2
Consideremos un pentágono con lados de l = 2.5 y apotema a = 1.72.
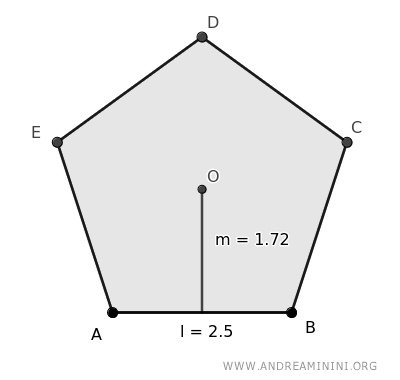
Nota: Un pentágono puede dividirse en 5 triángulos.
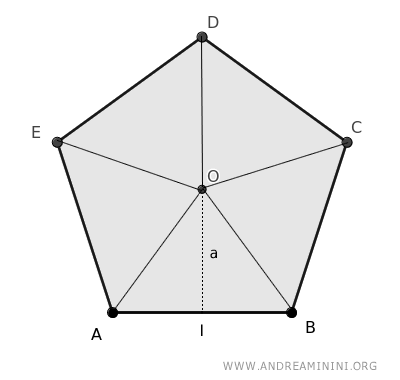
Primero calculamos el perímetro (P):
$$ P = 5 \cdot 2.5 = 12.5 $$
Luego, el semiperímetro (p):
$$ p = \frac{P}{2} = \frac{12.5}{2} = 6.25 $$
Y finalmente, el área:
$$ A = p \cdot a = 6.25 \cdot 1.72 = 10.75 $$
Así que el área del pentágono es A = 10.75.
Observaciones y notas
- Fórmulas inversas: A partir de $$ A = p \cdot a $$, se deducen: $$ p = \frac{A}{a} $$ $$ a = \frac{A}{p} $$ Y también: $$ P = 2p = \frac{2A}{a} $$
- El apotema es siempre perpendicular al lado. En un polígono regular, coincide con el radio de la circunferencia inscrita.
- Polígonos con muchos lados: Cuantos más lados tiene el polígono, más se aproxima a un círculo, y el apotema tiende a coincidir con el radio de dicho círculo.
- Relación entre apotema, radio y ángulos: El apotema, el radio y los ángulos internos están relacionados. Por ejemplo, en un hexágono regular, el ángulo central es 60° (360° ÷ 6). Usando trigonometría, se puede obtener el apotema a partir del radio y viceversa.
- Equivalencia entre un polígono regular y un triángulo: El área de un polígono regular es equivalente al área de un triángulo cuya base es el perímetro del polígono y cuya altura es el apotema.
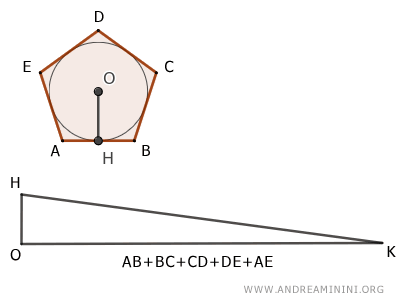
Y así sucesivamente.