Teorema de equivalencia entre un triángulo y un polígono inscrito en una circunferencia
Un triángulo OHK y un polígono ABCDE (regular o irregular) inscrito en una circunferencia son equivalentes $$ ABCDE \doteq OHK $$ si la altura del triángulo es igual al radio de la circunferencia y su base es igual al perímetro del polígono.
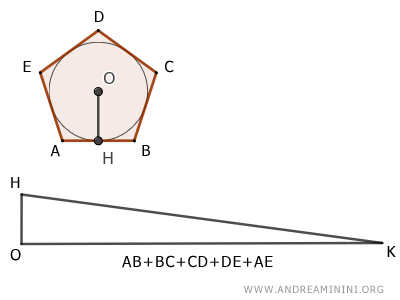
En términos geométricos, esto significa que en un polígono circunscrito el área puede calcularse como la de un triángulo cuya altura es el radio de la circunferencia y cuya base es el perímetro del polígono:
$$ Área = \frac{ \text{perímetro} \times \text{radio} }{2} $$
Dado que todo polígono regular es inscribible en una circunferencia, se deduce que todo polígono regular es equivalente a un triángulo.
En cambio, solo algunos polígonos irregulares pueden inscribirse en una circunferencia.
En la práctica, esto permite calcular el área de dichos polígonos como si se tratara de un triángulo con base y altura determinadas. Para demostrar el teorema, basta con descomponer el polígono en triángulos cuyas alturas coinciden con el radio de la circunferencia.
Un ejemplo
Consideremos un pentágono regular ABCDE con lados de 2 unidades.
El pentágono está inscrito en una circunferencia de radio OH = 1.38.
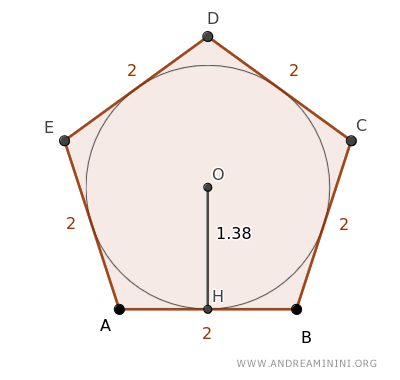
Al ser un polígono circunscrito, podemos aplicar el teorema de equivalencia para calcular su área como si fuera un triángulo.
El perímetro del pentágono es:
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EA} = 2 + 2 + 2 + 2 + 2 = 10 $$
Por tanto, consideramos un triángulo FGI con base FG = 10 (equivalente al perímetro del polígono, FG ≅ P) y altura IF = 1.38 (equivalente al radio, IF ≅ OH):
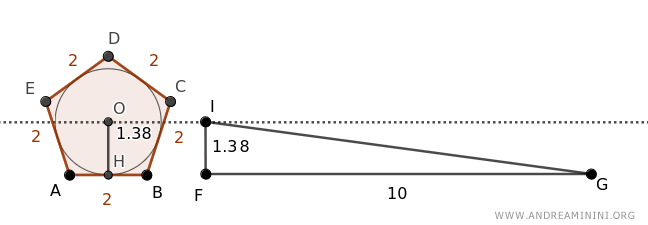
El área del triángulo es:
$$ A_t = \frac{b \cdot h}{2} = \frac{10 \cdot 1.38}{2} = \frac{13.8}{2} = 6.9 $$
Por lo tanto, el área del triángulo equivalente es:
$$ A_t = 6.9 $$
Y, en consecuencia, el área del pentágono también es:
$$ A_p = A_t = 6.9 $$
Hemos obtenido así el área del pentágono sin necesidad de calcularla directamente.
Como comprobación, podemos calcular el área del pentágono regular con la fórmula: $$ A_p = \frac{n \cdot l \cdot a}{2} $$ donde n = 5 es el número de lados, l = 2 es la longitud de cada lado y a = 1.38 es el apotema. $$ A_p = \frac{5 \cdot 2 \cdot 1.38}{2} = \frac{13.8}{2} = 6.9 $$ El resultado es idéntico.
Demostración
Consideremos un polígono ABCDE inscrito en una circunferencia de centro O y radio OH.
El número de lados y el hecho de que sea regular o irregular no afecta, siempre que sea inscrito.
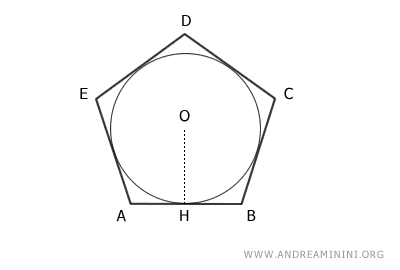
El perímetro es:
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EA} $$
Unimos el centro O con todos los vértices del polígono:
De este modo queda dividido en cinco triángulos: ABO, BCO, CDO, DEO, AEO.