Sumar y restar áreas
Para sumar las áreas de dos superficies, basta medir sus áreas respectivas A1 y A2 y sumar dichos valores: A1 + A2. Esto es válido siempre que las superficies no se superpongan.
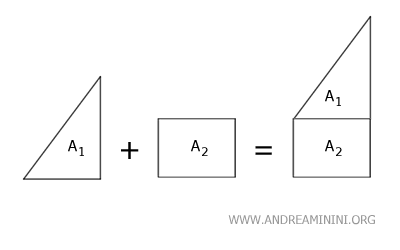
De igual modo, es posible calcular la diferencia de áreas restando el área de la segunda superficie (sustraendo) del área de la primera (minuendo).
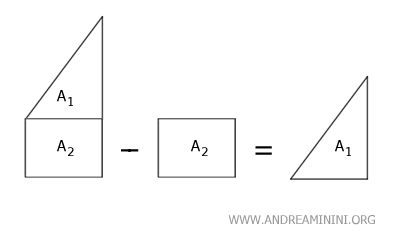
En esencia, el procedimiento consiste simplemente en sumar o restar las áreas de las dos superficies.
Sin embargo, es fundamental que las superficies no se superpongan, es decir, que no compartan puntos interiores en común.
Si existiera superposición, no sería posible realizar de forma correcta la suma o la resta de sus áreas.
Nota: En caso de superposición, la región común solo debe contabilizarse una vez en la suma total. Si se sumaran directamente ambas áreas A1 + A2, la intersección de las superficies (zona roja) se estaría contando dos veces.
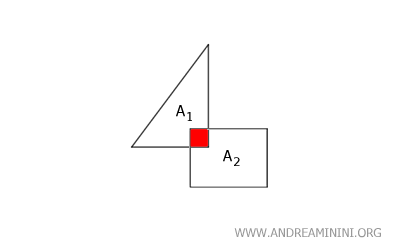
Además, se asume que ambas superficies se encuentran en el mismo plano bidimensional.
Un ejemplo práctico
Consideremos una superficie con un área de A1 = 6 metros cuadrados y otra con un área de A2 = 12 metros cuadrados.
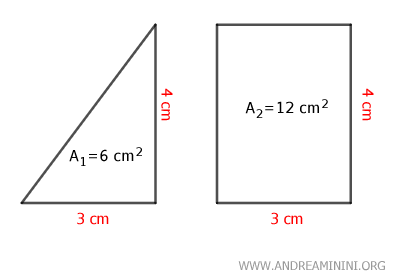
La suma de sus áreas es 18 metros cuadrados:
$$ A_1 + A_2 = 6 \ cm^2 + 12 \ cm^2 = 18 \ cm^2 $$
La diferencia de sus áreas es 6 metros cuadrados:
$$ A_2 - A_1 = 12 \ cm^2 - 6 \ cm^2 = 6 \ cm^2 $$
Conviene subrayar que la suma de las áreas es independiente de la forma de las superficies. Lo mismo se aplica a la resta.
Ya se trate de triángulos, rectángulos, círculos o cualquier otra figura, lo que verdaderamente importa es el valor del área de cada superficie.
Observaciones adicionales
A continuación, algunas propiedades adicionales relativas a la suma y la resta de áreas:
- La suma de dos áreas cumple la propiedad conmutativa de la adición: $$ A_1 + A_2 = A_2 + A_1 $$
- La suma de varias áreas cumple la propiedad asociativa de la adición: $$ A_1 + (A_2 + A_3) = (A_1 + A_2) + A_3 $$
Y así sucesivamente.