Superficies en geometría

En geometría, una superficie es una extensión bidimensional que posee longitud y anchura, pero carece de profundidad. Dicho de otro modo, una superficie es una región del plano delimitada por una o varias líneas cerradas que no se cruzan entre sí.

El concepto de superficie es una noción intuitiva en la geometría elemental. Con "intuitiva" se entiende que es un concepto primitivo, es decir, que no admite una definición formal rigurosa, al igual que sucede con los conceptos de punto, línea o plano.

Una superficie puede ser cerrada o abierta.

• Superficie cerrada
  Es aquella que está contenida en un espacio finito, delimitada por un contorno (por ejemplo, figuras geométricas cerradas, polígonos, etc.). Un anillo circular es un ejemplo de superficie cerrada, limitada por dos curvas cerradas no secantes. En estos casos, su área siempre puede calcularse.
  
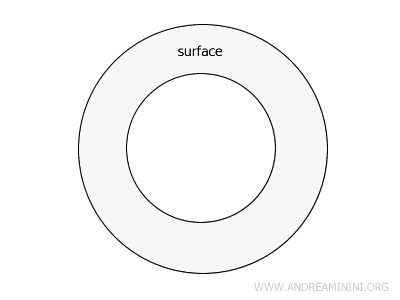
• Superficie abierta
  Es una superficie que se extiende indefinidamente en una o más direcciones (por ejemplo, un plano, un semiplano o la región comprendida entre dos líneas paralelas) dentro del espacio euclidiano bidimensional (x;y). Por lo tanto, su área es infinita y no es calculable.
  

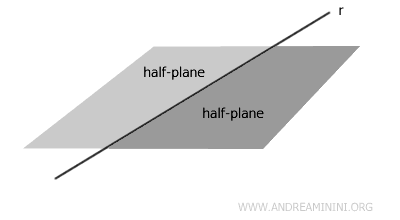
En general, cuando se habla de "superficie" en geometría, salvo que se indique lo contrario, se hace referencia a la superficie limitada y cerrada de una figura plana.

Nota: También puede entenderse una superficie como un conjunto de puntos en el espacio euclidiano tridimensional (x;y;z). De hecho, la noción de superficie surge de la necesidad de medir el contorno de un sólido. Por ejemplo, en un cubo, la superficie corresponde a la suma de las áreas de los cuadrados que forman sus caras.

Tipos de superficies

Existen dos tipos principales de superficies: planas y curvas.

• Superficies planas
  Una superficie plana es aquella que no presenta ninguna curvatura, extendiéndose de manera uniforme y continua en todas las direcciones dentro de un mismo plano. Puede estar limitada a una región finita o no. En un contexto más abstracto y matemático, corresponde al concepto de plano, una entidad ideal que se extiende infinitamente.

  Un ejemplo cotidiano de superficie plana sería una hoja de papel. Sin embargo, hay que recordar que una hoja de papel tiene un grosor físico, aunque sea mínimo. Una superficie plana, en cambio, es un concepto puramente geométrico que carece de grosor. En geometría plana, el grosor de la superficie se considera despreciable, incluso si existe físicamente.

• Superficies curvas
  A diferencia de las superficies planas, las superficies curvas presentan variaciones en su forma. No son planas. Pueden estar limitadas a una región concreta o extenderse infinitamente en todas direcciones. Desde el punto de vista geométrico, las superficies curvas son más complejas que las planas.

  Entre los ejemplos más conocidos de superficies curvas se encuentran la superficie de una esfera o la de un cilindro. Ambas son superficies cerradas que delimitan un volumen en el espacio euclidiano. Las superficies curvas se estudian dentro del marco de las geometrías no euclidianas.
  

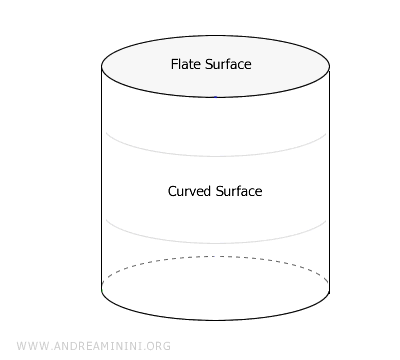
Más allá de estas categorías, las matemáticas modernas consideran también superficies en espacios de más de tres dimensiones. Estos conceptos, que escapan a nuestra intuición visual, resultan fundamentales en campos como la topología.

Superficies equivalentes

Dos superficies se consideran equivalentes cuando tienen la misma extensión, es decir, la misma área.

Por ejemplo, un triángulo y un cuadrado son superficies equivalentes si tienen la misma área, aunque sus formas sean distintas y no sean figuras congruentes.

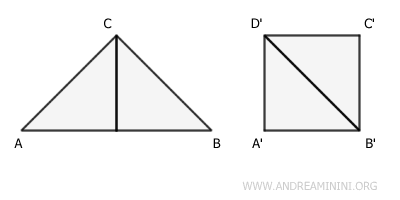
Cuando dos superficies son equivalentes, pertenecen a la misma clase de equivalencia.

Nota: Este ejemplo ilustra además que la equivalencia entre dos figuras no implica que sean congruentes. Las figuras congruentes son siempre equivalentes, pero no ocurre necesariamente a la inversa: dos figuras equivalentes no tienen por qué ser congruentes.

Suma y diferencia de superficies

La suma de dos superficies disjuntas S₁ y S₂ equivale a la suma de sus respectivas áreas: Área(S₁)+Área(S₂).

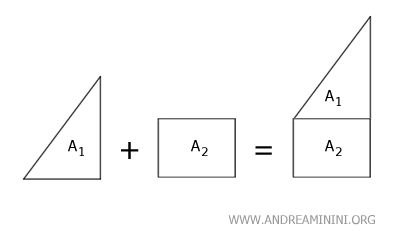
Del mismo modo, la diferencia entre dos superficies disjuntas S₁ y S₂ corresponde a la diferencia de sus áreas: Área(S₁)-Área(S₂).

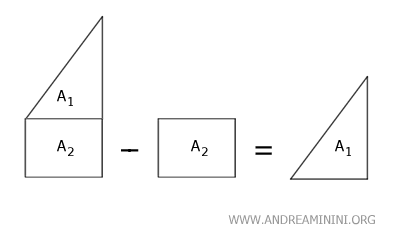
Comparación de superficies

Al comparar superficies, pueden darse las siguientes situaciones:

• Superficies equivalentes
  Son equivalentes si poseen la misma extensión (área).
  
• Superficie mayor
  Una superficie es mayor cuando su extensión (área) es superior a la de otra, es decir, ocupa un espacio mayor.
  
• Superficie menor
  Una superficie es menor cuando su extensión (área) es inferior a la de otra, es decir, ocupa un espacio menor.
  

Y así sucesivamente.