Polígonos equivalentes
Dos polígonos se denominan polígonos equivalentes cuando poseen la misma área.
La característica esencial de los polígonos equivalentes es que tienen idéntica extensión superficial.
Estos polígonos pueden presentar formas y tamaños muy diversos: pueden ser regulares o irregulares, convexos o cóncavos, y así sucesivamente.
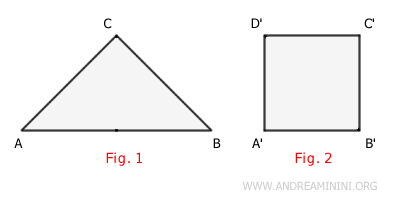
Lo que realmente importa es que sus áreas sean iguales, es decir, que ocupen la misma porción del plano.
Nota: Esta relación de equivalencia entre dos polígonos también se conoce como equi-extensión.
En consecuencia, dos polígonos equivalentes son también polígonos equicomponibles.
En otras palabras, es posible descomponer ambos polígonos en un conjunto de piezas más pequeñas, de modo que cada parte de uno sea congruente con una parte del otro, y viceversa.
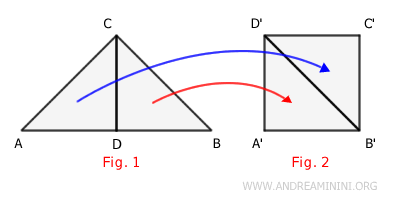
Este principio tiene aplicaciones tanto teóricas como prácticas, por ejemplo, para calcular áreas de polígonos irregulares mediante la descomposición en figuras más simples.
Mediante técnicas de corte y reordenación, es posible transformar un polígono en otro polígono equivalente.
Este concepto se formaliza en el teorema de Bolyai-Gerwien, que establece que cualquier polígono puede transformarse en otro polígono equivalente mediante un número finito de cortes y reordenamientos.
Criterios de equivalencia
En geometría existen varios criterios de equivalencia que permiten determinar si dos polígonos son equivalentes sin necesidad de calcular explícitamente sus áreas.
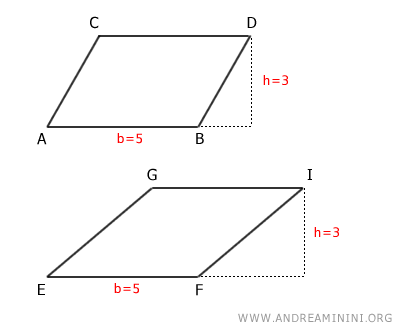
- Teorema de equivalencia de paralelogramos
Dos paralelogramos son equivalentes si comparten la misma base y la misma altura.
- Teorema de equivalencia de triángulos
Dos triángulos son equivalentes si tienen la misma base y la misma altura.
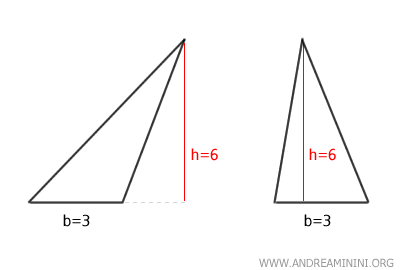
- Teorema de equivalencia entre un triángulo y un paralelogramo
Un triángulo es equivalente a un paralelogramo de igual altura y cuya base es la mitad de la base del triángulo.
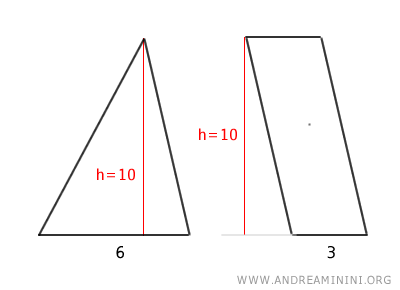
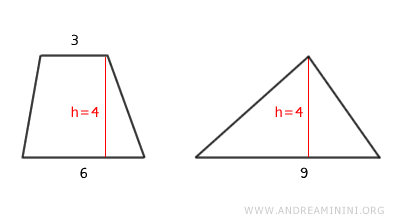
- Teorema de equivalencia entre un triángulo y un trapecio
Un trapecio es equivalente a un triángulo de igual altura y cuya base es igual a la suma de las bases del trapecio.
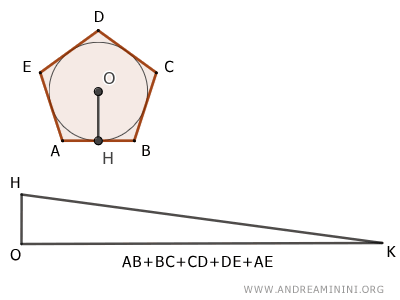
- Teorema de equivalencia entre un triángulo y un polígono circunscrito
Un polígono circunscrito a un círculo es equivalente a un triángulo cuya altura coincide con el radio de la circunferencia y cuya base es igual al perímetro del polígono.

El caso de los polígonos regulares: Dado que todo polígono regular puede circunscribirse en un círculo, se deduce que cualquier polígono regular es equivalente a un triángulo cuya altura es el radio de la circunferencia y cuya base es el perímetro del polígono.
Estos son solo algunos de los criterios de equivalencia que pueden aplicarse a las figuras planas.
Equivalencia y equicomponibilidad
En general, dos polígonos equivalentes son también equicomponibles, aunque la inversa no siempre se cumple.
El concepto de equivalencia en geometría es más amplio y no se limita exclusivamente al área: puede extenderse también al volumen.
Decimos que dos figuras planas o sólidas son "equivalentes" cuando poseen la misma medida, con independencia de su forma.
- En el caso de figuras planas (por ejemplo, polígonos), la medida es el área, es decir, la extensión superficial.
- En el caso de cuerpos sólidos (por ejemplo, poliedros), la medida es el volumen que ocupan en el espacio.
Este aspecto es importante, ya que equivalencia no implica necesariamente equicomponibilidad.
Ejemplo: Dos polígonos equivalentes pueden descomponerse y reordenarse para transformarse el uno en el otro, conservando la misma área. Sin embargo, en el caso de poliedros equivalentes con el mismo volumen, no siempre es posible descomponerlos y reordenarlos de modo que reproduzcan exactamente la forma del otro.
Observaciones
Algunas observaciones y notas complementarias:
- Teorema de Bolyai-Gerwien
Este teorema afirma que cualquier polígono puede descomponerse y recomponerse en otro polígono equivalente mediante un número finito de cortes y reordenaciones. - Polígono equivalente con un lado menos
Todo polígono convexo puede descomponerse y recomponerse en un polígono equivalente con un lado menos. - Triángulo equivalente
Cualquier polígono convexo puede transformarse en un polígono equivalente con un lado menos. Aplicando este principio de manera sucesiva, se deduce que cualquier polígono convexo con n > 3 lados puede reducirse a un triángulo equivalente con la misma área.
Y así sucesivamente.