Paralelogramo
Un paralelogramo es una figura geométrica plana de cuatro lados (un cuadrilátero) cuyos lados opuestos son paralelos y tienen la misma longitud (son congruentes).
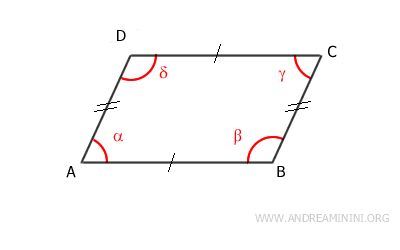
Estas son algunas de las propiedades más importantes de los paralelogramos:
- Los lados opuestos son paralelos y congruentes.
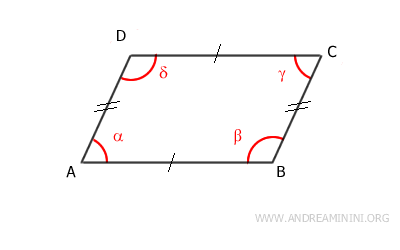
- Los ángulos opuestos son congruentes y miden lo mismo.
- Los ángulos contiguos en el mismo lado son suplementarios, es decir, suman 180°.
- Las diagonales se intersectan en su punto medio.
- Cada diagonal divide el paralelogramo en dos triángulos congruentes.
Entre los paralelogramos más comunes se encuentran los rectángulos y los rombos, que son casos particulares con propiedades adicionales.
El paralelogramo es una figura convexa, ya que puede interpretarse como la intersección de dos franjas no paralelas.
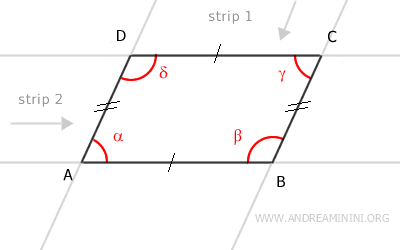
Se llama "franja" a la región del plano comprendida entre dos rectas paralelas.
Fórmulas esenciales de los paralelogramos
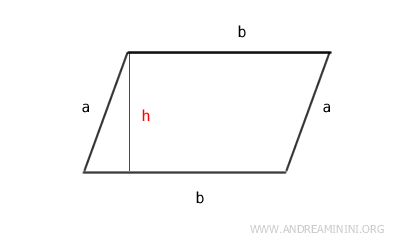
- El perímetro de un paralelogramo se obtiene multiplicando por dos la suma de la base (b) y el lado oblicuo (a). $$ P = 2 \cdot (a+b) $$
- El área de un paralelogramo se calcula multiplicando la base (b) por la altura (h): $$ A = b \cdot h $$
La base y la altura de un paralelogramo
En un paralelogramo, cualquiera de sus lados puede considerarse como la base (b), y uno de los lados adyacentes se toma como la altura (h).
La altura (h) es la distancia perpendicular que separa el lado opuesto de la base de la recta que contiene dicha base.
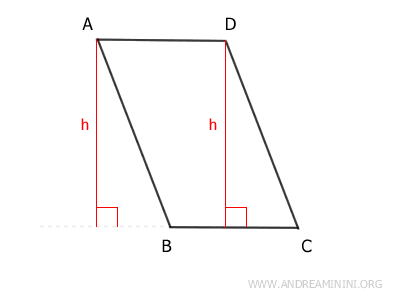
Por ejemplo, el segmento h representa la altura del paralelogramo ABCD si se escoge el lado AB como base.
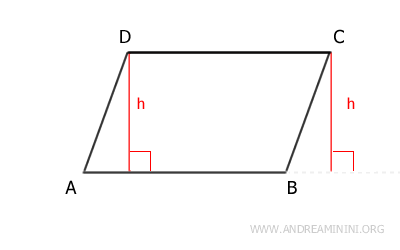
Por otro lado, si se toma el lado BC como base, las alturas (h) del paralelogramo se muestran a continuación:
Tipos de paralelogramos
Dentro de los paralelogramos se incluyen varias figuras geométricas muy conocidas, como los rectángulos, los rombos y los cuadrados.
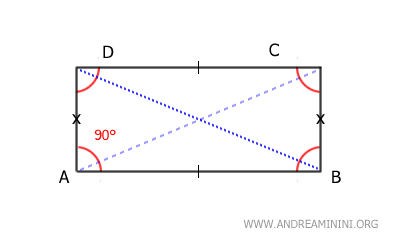
- Rectángulos
Los rectángulos son paralelogramos que se caracterizan por tener cuatro ángulos rectos (de 90°).
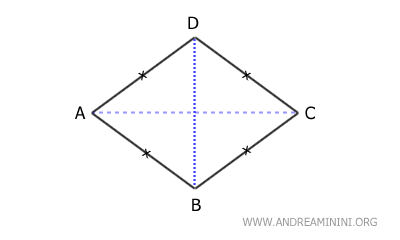
- Rombos
Los rombos son paralelogramos cuyos cuatro lados tienen la misma longitud y cuyas diagonales se cruzan perpendicularmente.
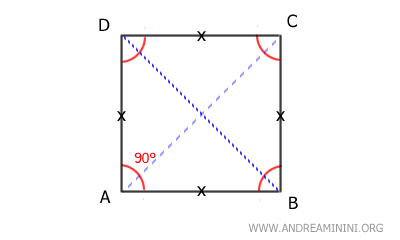
- Cuadrados
Los cuadrados son paralelogramos especiales que reúnen las propiedades tanto de los rectángulos como de los rombos. Tienen cuatro ángulos rectos, lados iguales y diagonales que se cruzan formando ángulos rectos.
Por lo tanto, los rectángulos, los rombos y los cuadrados son casos particulares de paralelogramos.
Las principales diferencias entre estas figuras se recogen en la siguiente tabla:
| Propiedad | Paralelogramo | Rectángulo | Rombo | Cuadrado |
|---|---|---|---|---|
| Lados opuestos congruentes | SÍ | SÍ | SÍ | SÍ |
| Ángulos opuestos congruentes | SÍ | SÍ | SÍ | SÍ |
| Ángulos adyacentes suplementarios | SÍ | SÍ | SÍ | SÍ |
| Las diagonales se cortan en el punto medio | SÍ | SÍ | SÍ | SÍ |
| Las diagonales dividen en triángulos congruentes | SÍ | SÍ | SÍ | SÍ |
| Las diagonales son congruentes | -- | SÍ | -- | SÍ |
| Las diagonales son perpendiculares | -- | -- | SÍ | SÍ |
| Las diagonales bisecan los ángulos | -- | -- | SÍ | SÍ |
| Todos los lados son congruentes | -- | -- | SÍ | SÍ |
| La suma de los ángulos interiores es 360° | SÍ | SÍ | SÍ | SÍ |
Teorema del Paralelogramo
Un cuadrilátero convexo es un paralelogramo si cumple al menos uno de los siguientes criterios:
- Sus lados opuestos son congruentes.
- Sus ángulos opuestos son congruentes.
- Sus diagonales se cortan en el punto medio.
- Dos lados opuestos son a la vez congruentes y paralelos.
Si se cumple cualquiera de estas condiciones, las demás quedan automáticamente satisfechas.
Por tanto, para determinar si un cuadrilátero es un paralelogramo, basta con comprobar que al menos una de estas condiciones se cumple.
Cómo construir un paralelogramo
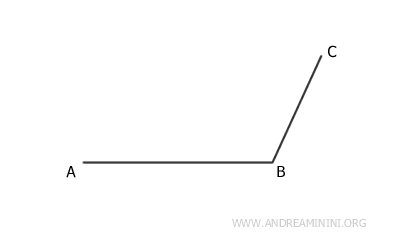
Primero, dibuja dos lados consecutivos del paralelogramo.
Empieza trazando el lado más largo AB y, a continuación, el lado más corto BC (o en el orden inverso).
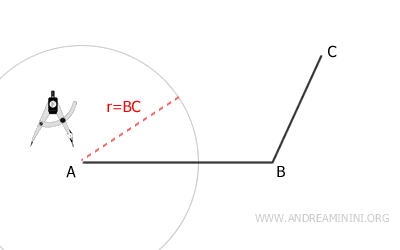
Coloca el compás en el vértice A y, con un radio igual a BC, traza el primer arco.
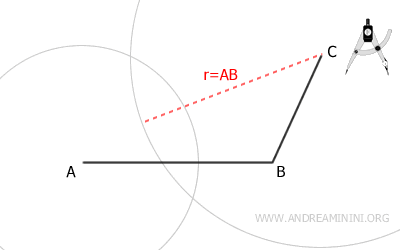
Luego, sitúa el compás en el vértice C y, con radio igual a AB, dibuja el segundo arco.
Los dos arcos pueden cortarse en dos puntos distintos: D y E.
Sin embargo, solo uno de esos puntos (D) dará lugar a un polígono convexo, por lo que el otro punto (E) se descarta.
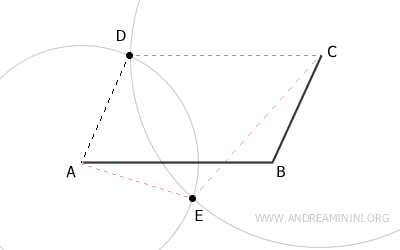
En este caso, el punto D es el cuarto vértice del paralelogramo.
Ahora, dibuja el segmento CD.
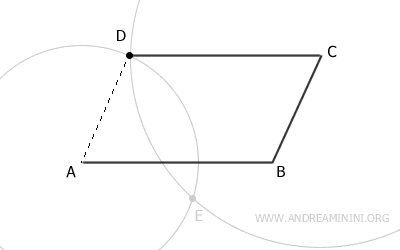
Por último, dibuja el segmento AD, que es el cuarto y último lado del cuadrilátero.
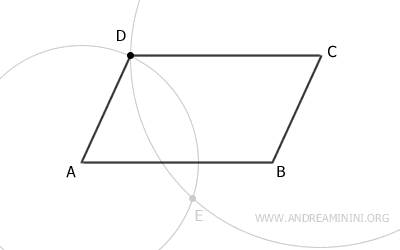
El resultado es un paralelogramo, un cuadrilátero cuyos lados opuestos son paralelos y congruentes.
Observaciones
Algunas notas y propiedades importantes sobre los paralelogramos:
- Cada lado y cada diagonal del paralelogramo puede considerarse como una transversal que corta dos rectas paralelas.
Esto permite aplicar los teoremas de las rectas paralelas para determinar los ángulos del paralelogramo o en demostraciones geométricas.
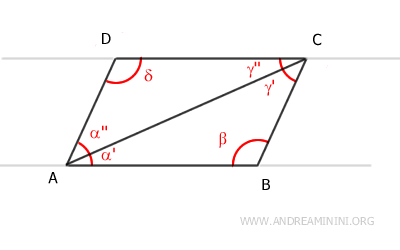
- Cada diagonal divide el paralelogramo en dos triángulos congruentes
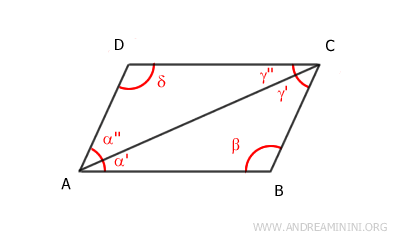
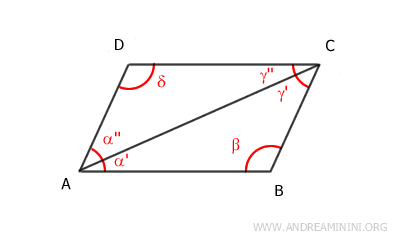
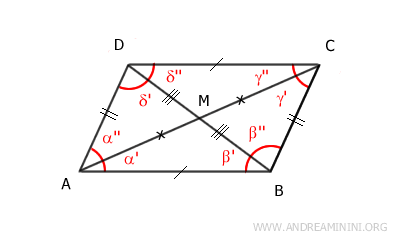
Demostración: Consideremos la diagonal mayor que va del vértice A al vértice C. Esta diagonal divide el paralelogramo en dos triángulos, ACD y ABC. La diagonal AC es lado común a ambos. Según el teorema de las rectas paralelas, los ángulos α' y γ'' son congruentes α'≅γ'' porque son ángulos alternos internos formados por los segmentos AB y CD, cortados por la transversal AC. De igual forma, los ángulos α'' y γ' son congruentes α''≅γ' por el mismo motivo: también son ángulos alternos internos. Por lo tanto, según el segundo criterio de congruencia de triángulos (ASA), los triángulos ACD y ABC son congruentes ACD≅ABC.
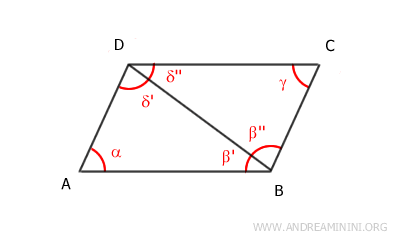
Ahora consideremos la diagonal menor que une el vértice B con el vértice D. Esta diagonal divide el paralelogramo en dos triángulos, ABD y BCD. La diagonal BD es lado común a ambos. Según el teorema de las rectas paralelas, los ángulos β' y δ'' son congruentes β'≅δ'' porque son ángulos alternos internos formados por los segmentos AB y CD, cortados por la transversal BD. De igual modo, los ángulos β'' y δ' son congruentes β''≅δ' por la misma razón: también son ángulos alternos internos. Por lo tanto, según el segundo criterio de congruencia de triángulos (ASA), los triángulos ABD y BCD son congruentes ABD≅BCD.
- Los lados opuestos de un paralelogramo son congruentes
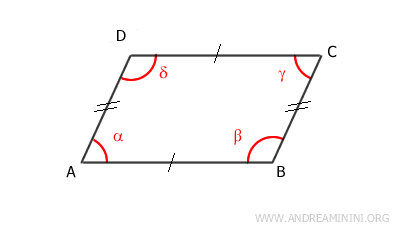
Demostración: Una diagonal divide el paralelogramo en dos triángulos congruentes: ACD≅ABC. Dado que estos triángulos son congruentes, sus lados correspondientes también lo son en el mismo orden: CD≅AB y AD≅BC, siendo AC el lado común. Esto demuestra que los lados opuestos de un paralelogramo son congruentes.
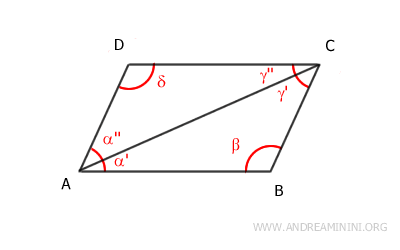
- Los ángulos opuestos de un paralelogramo son congruentes
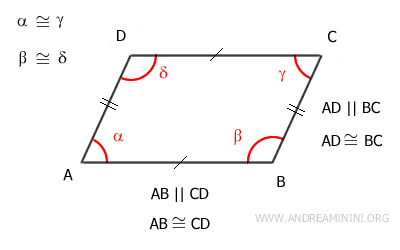
Demostración: La diagonal mayor AC divide el paralelogramo en dos triángulos congruentes: ACD≅ABC. En consecuencia, los ángulos correspondientes de estos triángulos también son congruentes: β≅δ, γ'≅α'', α'≅γ''. Es importante destacar que los ángulos β≅δ son congruentes por ser opuestos en el paralelogramo.
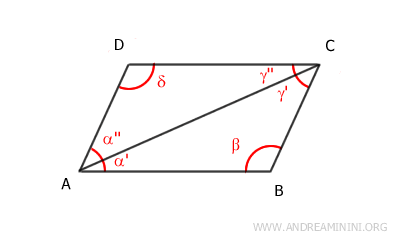
De igual manera, la diagonal menor BD divide el paralelogramo en dos triángulos congruentes: ADB≅BCD. En este caso, los ángulos correspondientes también son congruentes: α≅γ, β'≅δ'', δ'≅β''. En particular, es importante resaltar que los ángulos α≅γ son congruentes por ser ángulos opuestos en el paralelogramo.
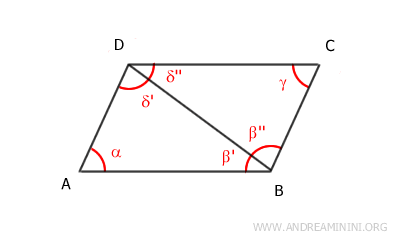
- Los ángulos adyacentes en un paralelogramo son suplementarios (180°)
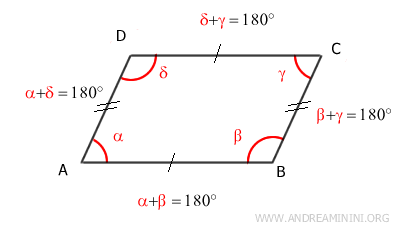
Demostración: Los ángulos α y β son adyacentes al lado AB. Según el teorema de las rectas paralelas, los ángulos α y β son suplementarios (α+β=180°) porque son ángulos correspondientes de las rectas paralelas AD||BC cortadas por la transversal AB. El mismo razonamiento se aplica al resto de pares de ángulos adyacentes en el paralelogramo.
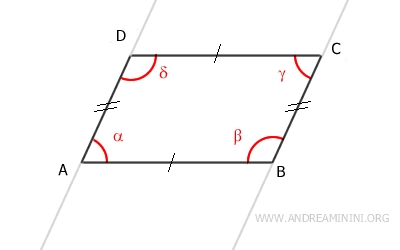
Esto demuestra que todos los ángulos adyacentes en un paralelogramo son ángulos suplementarios $$ \alpha + \beta = 180° $$ $$ \alpha + \delta = 180° $$ $$ \beta + \gamma = 180° $$ $$ \gamma + \delta = 180° $$ - Las diagonales se intersectan en su punto medio
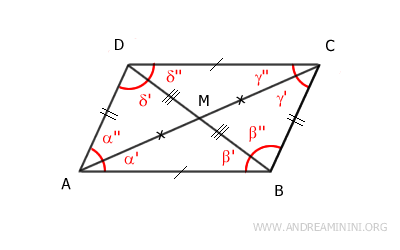
Demostración: Dibuja las dos diagonales AC y BD del paralelogramo. Los lados opuestos del paralelogramo son congruentes AB≅CD y AD≅BC. Según el teorema de las rectas paralelas, los ángulos α'≅γ'' son congruentes por ser ángulos alternos internos formados por las rectas paralelas AB||CD cortadas por la recta AC. De igual forma, los ángulos β'≅δ'' son congruentes porque son ángulos alternos internos formados por las mismas paralelas cortadas por la recta BD.
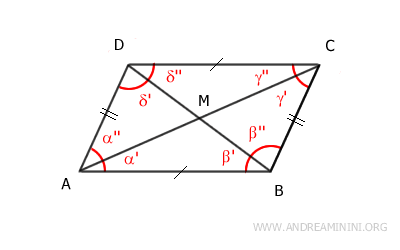
Por tanto, según el segundo criterio de congruencia de triángulos, los triángulos ABM y CDM son congruentes, ya que tienen un lado congruente AB≅CD y dos ángulos congruentes α'≅γ'' y β'≅δ''. En consecuencia, los lados correspondientes de estos triángulos son iguales. En particular, se cumple que los segmentos AM≅MC y BM≅DM son congruentes. Esto significa que el punto M es el punto medio de ambas diagonales, dividiéndolas en dos partes iguales.
Y así sucesivamente.