Teorema del Paralelogramo
Un cuadrilátero convexo se clasifica como un paralelogramo si cumple al menos una de las siguientes condiciones:
- Sus lados opuestos son congruentes
- Sus ángulos opuestos son congruentes
- Dos lados opuestos son, a la vez, congruentes y paralelos
- Sus diagonales se bisecan mutuamente
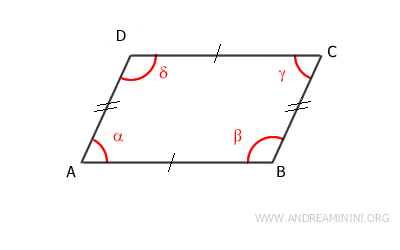
Cualquiera de estas condiciones es suficiente para determinar que un cuadrilátero es un paralelogramo.
Además, si se cumple una de ellas, las demás se verifican automáticamente.
Nota: Es importante destacar que el término «convexo» es clave en esta definición, ya que un paralelogramo es, por definición, un cuadrilátero convexo cuyos lados opuestos son paralelos y congruentes.
Demostración
La demostración se desarrolla en cuatro apartados principales.
1] Un cuadrilátero es un paralelogramo si sus lados opuestos son congruentes
En este caso, partimos del supuesto de que los lados opuestos son congruentes: AB≅CD y AD≅BC.
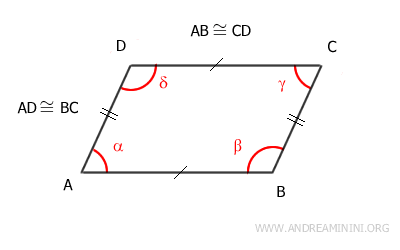
Para demostrar que el cuadrilátero es un paralelogramo, debemos probar que sus lados opuestos no solo son congruentes, sino también paralelos.
Vamos a trazar una diagonal que una dos vértices opuestos, por ejemplo, la diagonal AC.
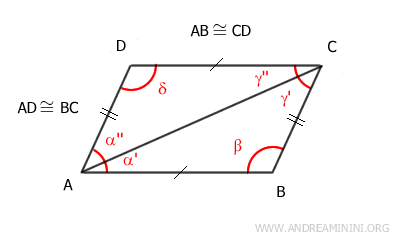
Esta diagonal divide el cuadrilátero en dos triángulos: ABC y ACD.
Los triángulos ABC y ACD son congruentes según el tercer criterio de congruencia de triángulos, ya que comparten:
- Un lado común (AC)
- Dos pares de lados congruentes, según nuestro supuesto: AB≅CD y AD≅BC
Como los dos triángulos son congruentes:
$$ ABC \cong ACD $$
Podemos afirmar que tienen ángulos correspondientes congruentes:
$$ \alpha ' = \gamma '' $$
$$ \alpha '' = \gamma ' $$
$$ \delta = \beta $$
Los ángulos α'≅γ'' son congruentes y, además, son ángulos alternos internos formados por las rectas AB y CD, cortadas por la transversal AC.
De acuerdo con el recíproco del teorema de las rectas paralelas, los ángulos alternos internos solo son congruentes si la transversal corta a dos rectas paralelas.
Por lo tanto, las rectas AB y CD son paralelas: AB||CD.
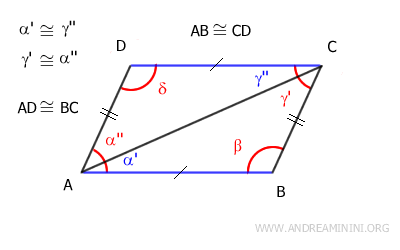
Del mismo modo, los ángulos γ'≅α'' son congruentes y son ángulos alternos internos formados por las rectas AD y BC, cortadas por la transversal AC.
Así, según el recíproco del teorema de las rectas paralelas, las rectas AD y BC son paralelas: AD||BC.
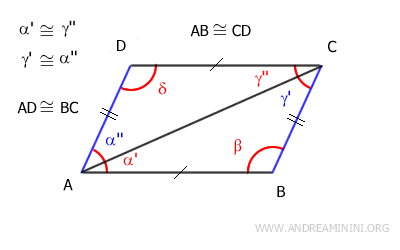
Tras demostrar que los lados AB||CD y AD||BC son paralelos, y sabiendo, por el supuesto inicial, que estos lados también son congruentes (AB≅CD y AD≅BC), podemos concluir que el cuadrilátero es un paralelogramo.
2] Un cuadrilátero es un paralelogramo si sus ángulos opuestos son congruentes
En este caso, partimos del supuesto de que los ángulos opuestos son congruentes: α≅γ y β≅δ.
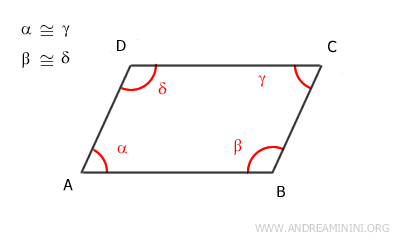
Para demostrar que se trata de un paralelogramo, debemos probar que sus lados opuestos son paralelos y congruentes.
Se trata de un polígono convexo de cuatro lados (n=4), por lo que, según el teorema de la suma de ángulos interiores en un polígono convexo, la suma de sus ángulos interiores es (n-2)·180°=360°.
$$ \alpha + \beta + \gamma + \delta = 360° $$
Dado que los ángulos α≅γ y β≅δ son congruentes,
Podemos afirmar que las sumas de pares de ángulos también son congruentes, por lo que se cumple:
$$ \alpha + \beta \cong \gamma + \delta $$
$$ \alpha + \delta \cong \gamma + \beta $$
Como sabemos que α+β+γ+δ=360°, deducimos que las igualdades α+β=180° y α+δ=180° son ciertas.
$$ \alpha + \beta = 180° $$
$$ \alpha + \delta = 180° $$
Por lo tanto, los ángulos α y β, así como los ángulos α y δ, son suplementarios, ya que α+β=180° y α+δ=180°.
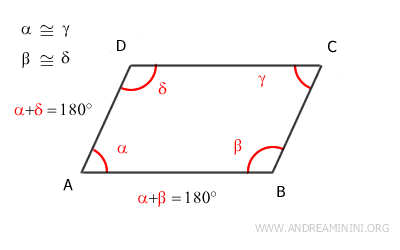
Los ángulos α y β son ángulos suplementarios (α+β=180°) y, además, son ángulos internos consecutivos formados por la intersección de las rectas AD y BC con la transversal AB.
Por tanto, según el recíproco del teorema de las rectas paralelas, los lados AD y BC son paralelos, es decir, AD||BC.
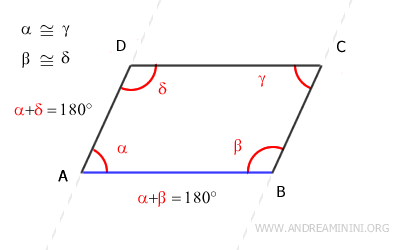
Del mismo modo, los ángulos α y δ son ángulos suplementarios (α+δ=180°) y también son ángulos internos consecutivos formados por las rectas AB y CD, cortadas por la transversal AD.
Así, nuevamente según el recíproco del teorema de las rectas paralelas, los lados AB y CD son paralelos, es decir, AB||CD.
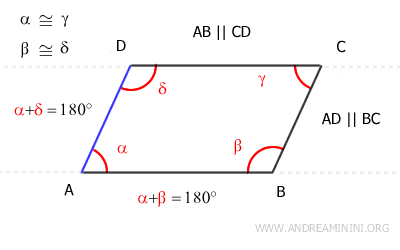
Una vez establecido que los lados opuestos del cuadrilátero son paralelos (AB||CD y AD||BC), el paso siguiente es demostrar que estos lados opuestos también son congruentes.
Para ello, trazamos la diagonal AC, que divide el cuadrilátero en dos triángulos: ABC y ACD.
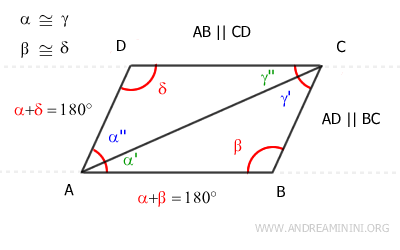
En este punto, aplicamos el teorema de las rectas paralelas:
- Como las rectas AD y BC son paralelas, los ángulos alternos internos α''≅γ' formados por la intersección con la transversal AC son congruentes.
- Del mismo modo, como las rectas AB y CD son paralelas, los ángulos alternos internos α'≅γ'' formados por la intersección con la transversal AC también son congruentes.
Esto permite concluir que los triángulos ABC y ACD son congruentes según el segundo criterio de congruencia de triángulos, puesto que:
- Comparten un lado común (AC).
- Tienen dos ángulos congruentes: α'≅γ'' y γ'≅α''.
Una vez demostrado que los triángulos ABC≅ACD son congruentes, se deduce que sus lados correspondientes son congruentes.
En particular, esto implica que los lados AD≅BC y AB≅CD son congruentes.
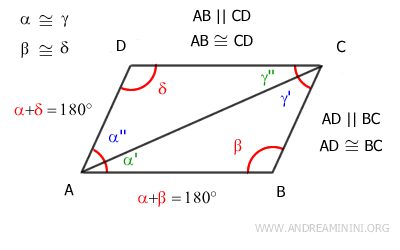
En conclusión, hemos demostrado que los lados opuestos del cuadrilátero son paralelos y congruentes.
Por tanto, el cuadrilátero es, efectivamente, un paralelogramo.
3] Un cuadrilátero tiene dos lados opuestos que son simultáneamente paralelos y congruentes
En este caso, partimos del supuesto de que dos lados opuestos son a la vez paralelos y congruentes.
Por ejemplo, AB≅CD y AB || CD.
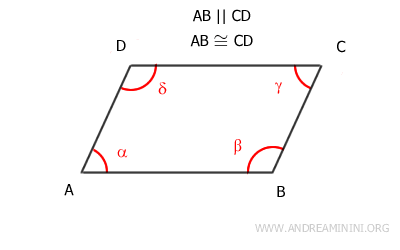
El objetivo es demostrar que los otros dos lados opuestos, AD y BC, también son paralelos y congruentes.
Para ello, comenzamos trazando la diagonal AC, que divide el cuadrilátero en dos triángulos: ABC y ACD.
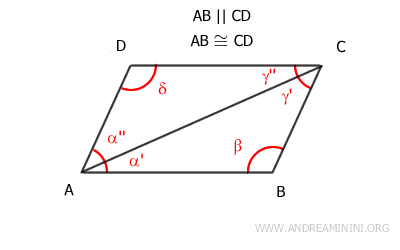
Como los segmentos AB y CD son paralelos según nuestro supuesto inicial (AB || CD), de acuerdo con el teorema de las rectas paralelas, los ángulos alternos internos α'≅γ' son congruentes.
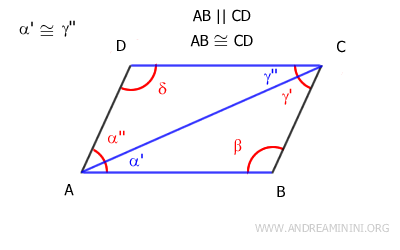
Esto nos permite concluir que los triángulos ABC y ACD son congruentes según el primer criterio de congruencia de triángulos, ya que:
- Poseen un lado congruente, AB≅CD, según el supuesto inicial.
- Comparten el lado AC (la diagonal).
- Tienen el ángulo α'≅γ' comprendido entre los lados mencionados.
Una vez establecido que los triángulos ABC≅ACD son congruentes, se deduce que todos sus lados y ángulos correspondientes también lo son.
En particular, esto implica que los lados AD≅BC son congruentes y que los ángulos α''≅γ' también lo son.
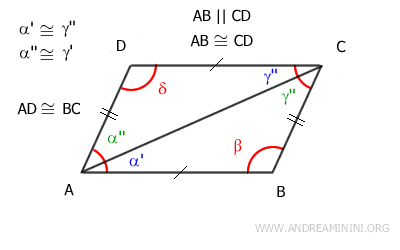
Hasta este punto, hemos demostrado que ambos pares de lados opuestos son congruentes: AB≅CD y AD≅BC.
Resta demostrar que los lados AD y BC también son paralelos.
Para ello, observamos que los ángulos α''≅γ' son congruentes y, además, son ángulos alternos internos formados por las rectas AD y BC al ser cortadas por la transversal AC.
Por lo tanto, según el recíproco del teorema de las rectas paralelas, los lados AD y BC son paralelos: AD || BC.
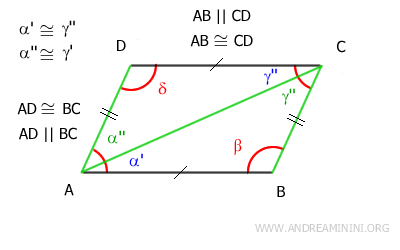
En conclusión, hemos demostrado que los lados opuestos del cuadrilátero son tanto paralelos como congruentes.
Por tanto, podemos afirmar que el cuadrilátero es un paralelogramo.
4] Un cuadrilátero es un paralelogramo si sus diagonales se bisecan mutuamente
Partimos aquí del supuesto de que las diagonales de un cuadrilátero convexo se cortan en su punto medio.
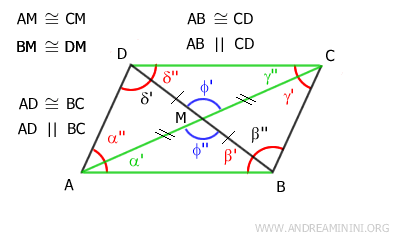
Así, los segmentos AM≅CM y BM≅DM son congruentes.
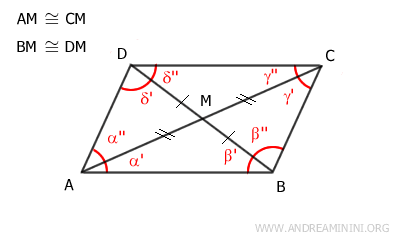
Para demostrar que el cuadrilátero es un paralelogramo, es necesario probar que sus lados opuestos son paralelos y congruentes.
Los ángulos θ' y θ'' son ángulos opuestos por el vértice, por lo que son congruentes: θ'≅θ''.
Esto nos permite concluir que los triángulos AMD y BMC son congruentes según el primer criterio de congruencia de triángulos, ya que tienen dos lados congruentes y el ángulo comprendido entre ellos también congruente.
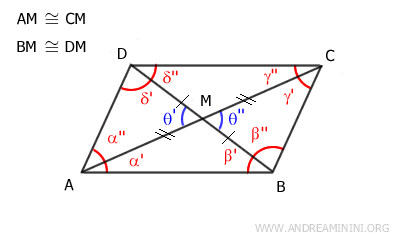
Una vez demostrado que los triángulos AMD≅BMC son congruentes, se deduce que los lados AD≅BC son congruentes.
Además, todos los ángulos de estos triángulos son congruentes en orden correspondiente.
En particular, conviene destacar que los ángulos δ'≅β' son congruentes, ya que también son ángulos alternos internos formados por las rectas AD y BC al ser cortadas por la transversal BD.
Por tanto, según el recíproco del teorema de las rectas paralelas, los lados AD y BC son paralelos: AD || BC.
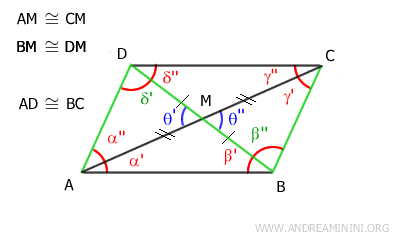
Podemos aplicar un razonamiento similar a los triángulos ABM y CDM.
Los ángulos φ' y φ'' son ángulos opuestos por el vértice, por lo que también son congruentes: φ'≡φ''.
En consecuencia, los triángulos ABM y CDM son congruentes según el primer criterio de congruencia de triángulos, ya que poseen dos lados congruentes y el ángulo comprendido también congruente.
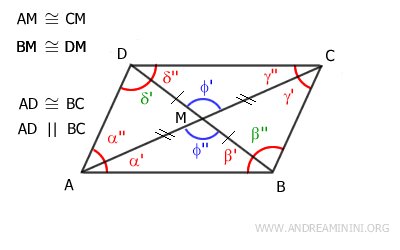
Una vez demostrado que los triángulos ABM≅CDM son congruentes, concluimos que los lados AB≅CD son congruentes.
Además, los ángulos de ambos triángulos son congruentes en orden correspondiente.
En particular, es relevante notar que los ángulos α'≅γ'' son congruentes, ya que también son ángulos alternos internos formados por las rectas AB y CD al ser cortadas por la transversal AC.
Por tanto, según el recíproco del teorema de las rectas paralelas, los lados AB y CD también son paralelos: AB || CD.
En conclusión, los lados opuestos del cuadrilátero son tanto congruentes como paralelos.
Por tanto, podemos afirmar con certeza que el cuadrilátero es un paralelogramo.
Y así sucesivamente.