Teorema de la Suma de los Ángulos Exteriores en Polígonos Convexos
En cualquier polígono convexo de $n$ lados, la suma de los ángulos exteriores (uno por vértice) es siempre igual a una vuelta completa (360°).
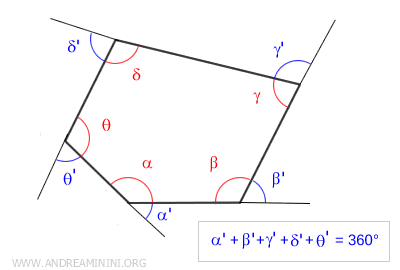
Dicho de otro modo, la suma de los ángulos exteriores de un polígono convexo se mantiene constante: no depende ni del número de lados ni de la forma concreta del polígono. Por eso, se considera un importante invariante.
Así, tanto en un triángulo, como en un cuadrado, un pentágono o cualquier polígono de $n$ lados, la suma de sus ángulos exteriores será siempre 360°.
Ejemplo: Imagina que caminas bordeando una cerca. La forma exacta de la cerca no importa: puede tener muchos ángulos o tan solo unos pocos. La única condición es que forme un polígono convexo. Cada vez que alcanzas una esquina, cambias de dirección.
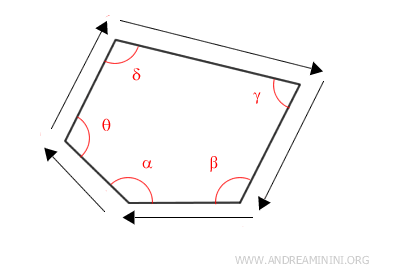
La suma total de todos esos cambios de dirección, al recorrer el perímetro, equivale exactamente a 360°, como si hubieras dado una vuelta completa alrededor de la cerca.
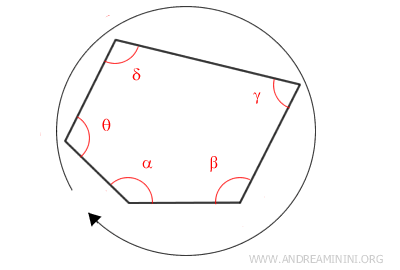
Demostración
Consideremos un polígono convexo.
Por ejemplo, uno de $n = 5$ lados.
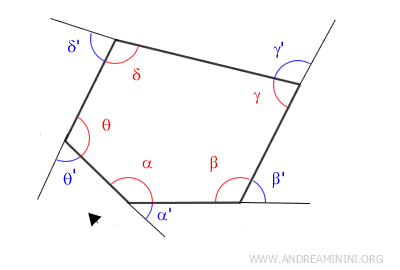
Cada ángulo exterior de un polígono convexo es adyacente a un ángulo interior.
Por tanto, cada ángulo exterior es suplementario con su ángulo interior adyacente, formando entre ambos un ángulo llano de 180°.
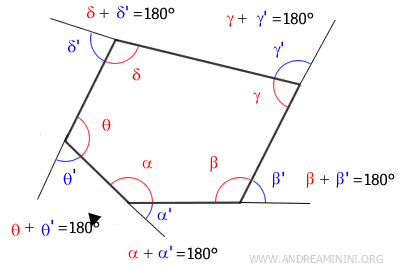
Esto implica que en un polígono convexo de $n$ lados hay $n$ pares de ángulos, y que la suma de todos los ángulos interiores y exteriores es $n \times 180°$.
$$ n \cdot 180° $$
Sabemos que la suma de los ángulos interiores es igual a $(n-2) \times 180°$. Por tanto, podemos hallar la suma de los ángulos exteriores restando esta cantidad del total.
En esencia, la suma de los ángulos exteriores se obtiene como la diferencia entre el total de ángulos interiores y exteriores y la suma de los ángulos interiores.
Así, la suma de los ángulos exteriores de un polígono convexo es:
$$ n \cdot 180° - [ (n-2) \cdot 180° ] $$
Con un simple cálculo algebraico, esto se simplifica así:
$$ [ n - (n-2) ] \cdot 180° = $$
$$ ( n - n + 2 ) \cdot 180° = $$
$$ 2 \cdot 180° = 360° $$
Por tanto, independientemente del número de lados, la suma de los ángulos exteriores de cualquier polígono convexo es siempre 360°.
¡Y eso es precisamente lo que afirma el teorema!
Notas
Aquí tienes algunos aspectos clave sobre la suma de los ángulos exteriores en un polígono convexo:
- La suma de los ángulos exteriores es un invariante más sólido que la suma de los ángulos interiores
La suma de los ángulos exteriores de cualquier polígono convexo es siempre 360°, siempre que se tome exactamente un ángulo exterior en cada vértice, sin importar cuántos lados tenga el polígono ni su forma. En cambio, la suma de los ángulos interiores sí depende del número de lados $n$ y se calcula mediante la fórmula $ (n-2) \cdot 180° $. Por ello, se considera un invariante más débil, pues varía al cambiar $n$.
Y así sucesivamente.