Rombo

Un rombo es un tipo de paralelogramo en el que todos sus lados tienen la misma longitud.

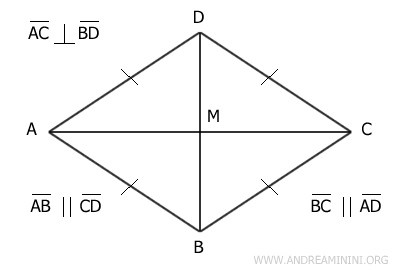
En otras palabras, un rombo es un cuadrilátero con cuatro lados iguales.

Al tratarse de un paralelogramo, el rombo comparte todas las propiedades básicas de este tipo de figuras:

• Sus lados opuestos son paralelos.
• Sus ángulos y lados opuestos son congruentes.
• Los ángulos contiguos son suplementarios, es decir, suman 180°.
• Sus diagonales se cortan en sus puntos medios.

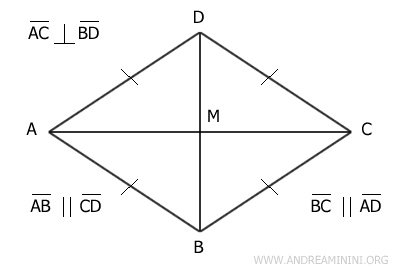
Además, el rombo posee algunas características particulares:

• Sus cuatro lados miden exactamente lo mismo.
• Sus diagonales son perpendiculares, formando entre ellas un ángulo recto de 90°.
• Las diagonales dividen los ángulos internos en partes iguales.

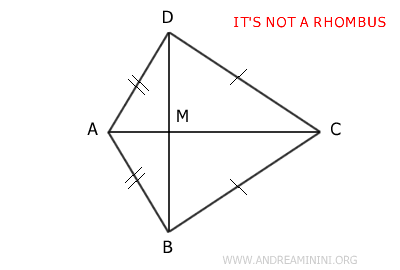
Aunque estas condiciones son necesarias, no bastan por sí solas para asegurar que un cuadrilátero sea un rombo.

Por ejemplo, un cuadrilátero puede tener diagonales perpendiculares sin ser un rombo (como ocurre en un cometa convexo). Para que una figura pueda clasificarse como rombo, además debe cumplir la condición de ser un paralelogramo.

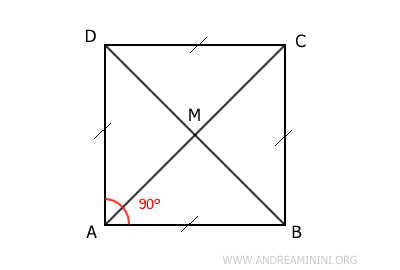
Por otro lado, el cuadrado comparte todas las propiedades de un rombo, pero se diferencia en que tiene sus cuatro ángulos rectos de 90°. Por eso, puede considerarse un caso particular de rombo. No obstante, en el uso cotidiano, una figura con esas características suele denominarse simplemente ‘cuadrado’.

Fórmulas del rombo

A continuación, se presentan algunas fórmulas útiles para calcular diversas propiedades de un rombo:

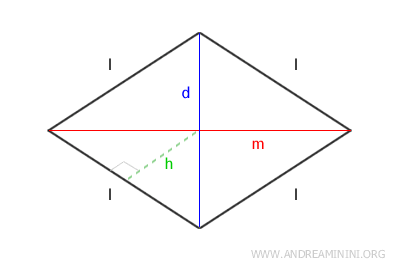
• Perímetro
  El perímetro de un rombo se obtiene multiplicando por cuatro la longitud de uno de sus lados. $$ P = 4 \cdot l $$
• Área
  El área de un rombo puede calcularse multiplicando las longitudes de sus diagonales (d y m) y dividiendo el resultado entre dos. $$ A = \frac{d \cdot m}{2} $$ Otra forma de hallarla, aprovechando que el rombo es un paralelogramo, es multiplicar la longitud del lado (l) por la altura (h). $$ A = l \cdot h $$
• Lado
  La longitud de un lado puede determinarse aplicando el teorema de Pitágoras. $$ l = \sqrt{ \left( \frac{d}{2} \right)^2 + \left( \frac{m}{2} \right)^2 } $$
• Diagonal mayor
  La fórmula de la diagonal mayor se deduce a partir de la fórmula del lado. $$ d = 2 \cdot \sqrt{ l^2 - \left(\frac{m}{2}\right)^2 } $$
• Diagonal menor
  De forma análoga, se obtiene la fórmula para la diagonal menor. $$ m = 2 \cdot \sqrt{ l^2 - \left(\frac{d}{2}\right)^2 } $$

  Explicación. Los pasos algebraicos para deducir las fórmulas de las diagonales mayor y menor del rombo son bastante sencillos. No obstante, para completitud, los detallo a continuación. Para hallar la diagonal mayor, partimos de la fórmula del lado: $$ l = \sqrt{ \left( \frac{d}{2} \right)^2 + \left( \frac{m}{2} \right)^2 } $$ Se aísla el término (d/l)² dentro de la raíz: $$ l = \frac{d}{2} + \sqrt{ \left( \frac{m}{2} \right)^2 } $$ Se despeja la diagonal mayor: $$ - \frac{d}{2} = -l + \sqrt{ \left( \frac{m}{2} \right)^2 } $$ Aplicamos la propiedad de invariancia y multiplicamos ambos miembros por -1: $$ - \frac{d}{2} \cdot (-1) = [ -l + \sqrt{ \left( \frac{m}{2} \right)^2 } ] \cdot (-1) $$ $$ \frac{d}{2} = l - \sqrt{ \left( \frac{m}{2} \right)^2 } $$ Se traslada el término l dentro de la raíz: $$ \frac{d}{2} = \sqrt{ l^2 - \left( \frac{m}{2} \right)^2 } $$ Finalmente, se vuelve a aplicar la propiedad de invariancia y se multiplican ambos lados por dos: $$ 2 \cdot \frac{d}{2} = 2 \cdot \sqrt{ l^2 - \left( \frac{m}{2} \right)^2 } $$ Así se obtiene la fórmula de la diagonal mayor: $$ d = 2 \cdot \sqrt{ l^2 - \left( \frac{m}{2} \right)^2 } $$ El mismo procedimiento se puede aplicar para deducir la fórmula de la diagonal menor: $$ m = 2 \cdot \sqrt{ l^2 - \left(\frac{d}{2}\right)^2 } $$

Cómo dibujar un rombo

Imagina que quieres dibujar un rombo cuya diagonal mayor mida 6 unidades y la menor, 4 unidades.

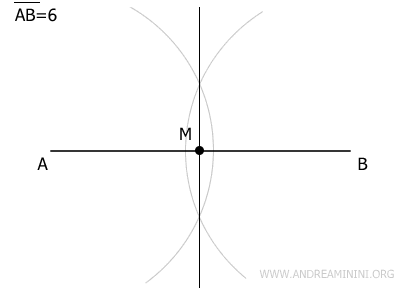
Comienza trazando un segmento AB de 6 unidades de longitud, que representará la diagonal mayor del rombo.

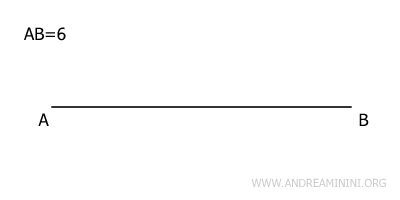
Después, dibuja una recta perpendicular al segmento AB.

Abre el compás a una distancia ligeramente superior a la mitad de AB, apóyalo en el punto A y traza un arco.

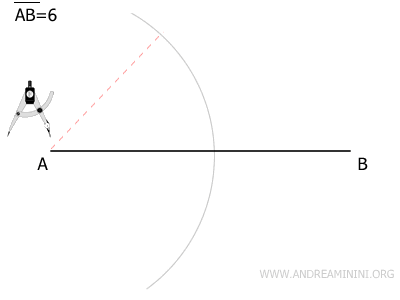
Sin variar la apertura del compás, colócalo en el punto B y traza otro arco que cruce el anterior en dos puntos distintos.

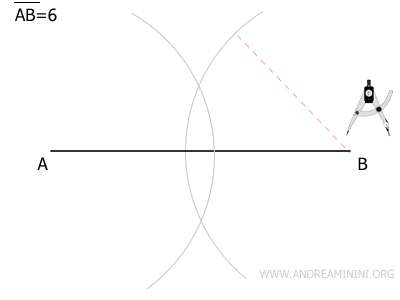
Traza una recta que pase por los puntos de intersección de los arcos. Esta recta será perpendicular al segmento AB.

El punto donde la recta perpendicular corta a AB es el punto medio M de la diagonal mayor del rombo.

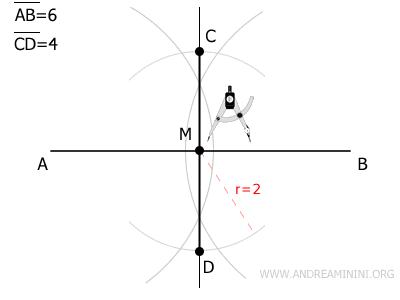
Ahora, dibuja la diagonal menor del rombo.

Coloca la punta del compás en M y traza un arco con radio igual a la mitad de la diagonal menor, es decir, 2 unidades.

Los puntos donde el arco corta a la recta perpendicular son los extremos C y D de la diagonal menor.

Finalmente, une los puntos A, B, C y D para formar el rombo, trazando los segmentos AC, AD, BC y BD.

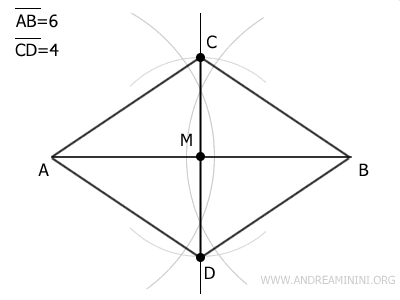
Siguiendo estos pasos, podrás construir un rombo, que es un paralelogramo de lados iguales, diagonales perpendiculares, con una diagonal mayor de 6 unidades y una menor de 4 unidades.

Notas Adicionales

A continuación, se presentan algunas observaciones y propiedades interesantes sobre el rombo:

• Un paralelogramo es un rombo si tiene dos lados consecutivos congruentes

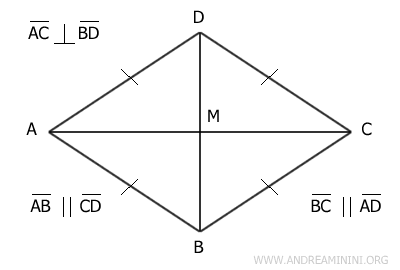
  Demostración. Dado que ABCD es un paralelogramo, sabemos que sus lados opuestos son congruentes; es decir, AB≅CD y AD≅BC. Si asumimos que dos lados consecutivos, por ejemplo AB y BC, también son congruentes (AB≅BC), por la propiedad transitiva se deduce que AB≅AD y BC≅CD. Así, los cuatro lados del paralelogramo son congruentes, lo que implica que ABCD es un rombo.

• Las diagonales de un rombo son perpendiculares y bisecan los ángulos

  Demostración. Consideremos un rombo ABCD, cuyas diagonales se cruzan en su punto medio M. Queremos demostrar que las diagonales AC y BD son perpendiculares y que además dividen los ángulos en partes iguales.
  
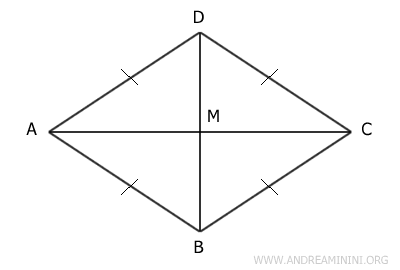
  Al ser un rombo, todos sus lados son congruentes. Esto hace que el triángulo ACD sea un triángulo isósceles, ya que sus lados AD y CD tienen la misma longitud. En un triángulo isósceles, la mediana correspondiente al vértice es también altura y bisectriz. Por tanto, el segmento DM actúa como bisectriz del ángulo D y, además, es perpendicular al lado AC, que en este caso es una de las diagonales del rombo.
  El mismo razonamiento se aplica al triángulo ABC, que es congruente con el triángulo ACD según el tercer criterio de congruencia de triángulos (Lado-Lado-Lado); es decir, ABC≅ACD. De ahí que la diagonal BD sea perpendicular a la diagonal AC y bisecte los ángulos en los vértices B y D.
  
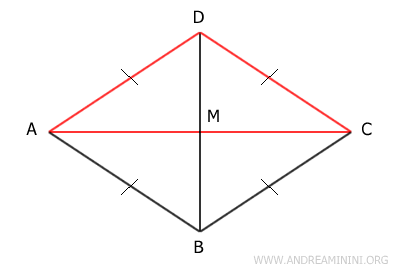
  Ahora analicemos el triángulo ABD, que también es un triángulo isósceles porque sus lados AD y AB son congruentes. Esto implica que el segmento AM es a la vez mediana, altura y bisectriz del ángulo en el vértice A. Así, divide dicho ángulo en dos partes iguales y es perpendicular a la diagonal BD. El mismo razonamiento vale para el triángulo BCD, que es congruente con ABD según el tercer criterio de congruencia, es decir, BCD≅ABD. En consecuencia, la diagonal AC biseca los ángulos en A y C, y es perpendicular a la diagonal BD.
  

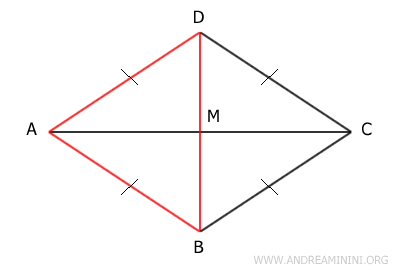
• Un paralelogramo es un rombo si sus diagonales son perpendiculares

  Demostración. Supongamos que ABCD es un paralelogramo cuyas diagonales AC y BD son perpendiculares entre sí. Como ABCD es un paralelogramo, sabemos que sus diagonales se cortan en el punto medio M. Por lo tanto, AM es congruente a CM, y BM es congruente a DM.
  
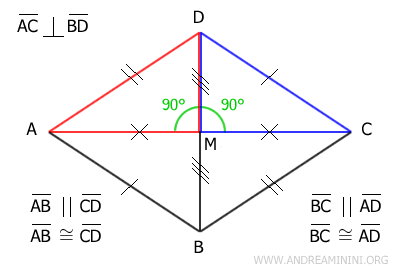
  Dado que AM≅CM y BM≅DM, los triángulos rectángulos AMD y CMD son congruentes (AMD≅CMD) por el primer criterio de congruencia, ya que comparten el lado DM, tienen lados congruentes y ángulos rectos congruentes. Al ser congruentes, todos sus lados y ángulos coinciden. En particular, sus hipotenusas AD y CD son congruentes, puesto que representan lados consecutivos del paralelogramo. De ahí se deduce que todos los lados del paralelogramo son congruentes, lo que confirma que se trata de un rombo.

• Un paralelogramo es un rombo si una de sus diagonales biseca un ángulo

  Demostración. Consideremos un paralelogramo ABCD. Supongamos que una de sus diagonales biseca uno de sus ángulos, por ejemplo, que la diagonal AC divide en dos partes iguales el ángulo en el vértice A. Entonces, los ángulos α' y α'' son congruentes.
  
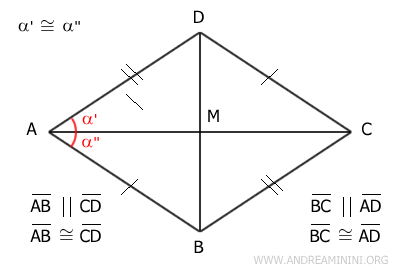
  Los lados opuestos de un paralelogramo siempre son paralelos, por lo que la diagonal AC actúa como transversal de las rectas paralelas AD||BC. Según el teorema de las rectas paralelas, los ángulos alternos internos son congruentes. Por tanto, los ángulos α' y γ son congruentes (α'≅γ).
  
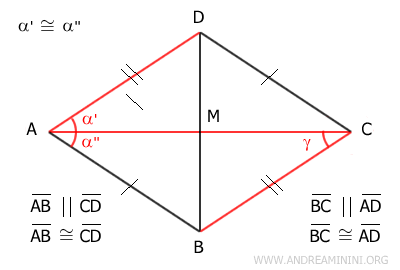
  Esto implica que el triángulo ABC tiene dos ángulos congruentes (α'≅γ) adyacentes al lado AC, lo que lo convierte en un triángulo isósceles con base AC. Siendo isósceles, sus lados oblicuos AB y BC son congruentes. Por tanto, el paralelogramo tiene dos lados consecutivos congruentes, lo cual implica que es un rombo.

• Una diagonal divide el rombo en dos triángulos isósceles congruentes

  Demostración. Un rombo tiene todos sus lados congruentes y diagonales perpendiculares. Además, al ser un paralelogramo, sus diagonales se cortan en su punto medio M. Cada diagonal divide el rombo en dos triángulos isósceles. Por ejemplo, la diagonal AC divide el rombo ABCD en los triángulos ACD y ABC. Estos triángulos tienen dos lados congruentes: AD≅CD y AB≅BC. Por tanto, ambos son triángulos isósceles. Además, según el tercer criterio de congruencia (Lado-Lado-Lado), son congruentes: ACD≅ABC, ya que sus lados son idénticos.
  
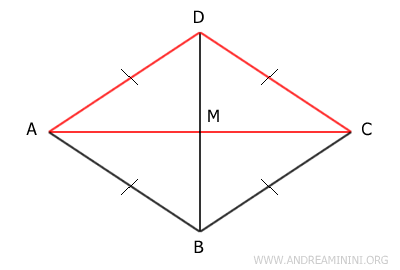
  La otra diagonal, BD, también divide el rombo en dos triángulos: ABD y BCD. Sus lados congruentes son AB≅AD y BC≅CD. Por tanto, ambos son triángulos isósceles. Además, como los tres lados son congruentes, por el tercer criterio de congruencia (Lado-Lado-Lado), los triángulos ABD≅BCD son congruentes.
  

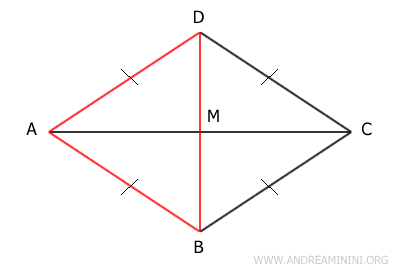
• Las diagonales dividen el rombo en cuatro triángulos rectángulos congruentes

  Demostración. Un rombo tiene todos sus lados congruentes y sus diagonales se cruzan de manera perpendicular en el punto medio M. Por el tercer criterio de congruencia (Lado-Lado-Lado), los triángulos AMD y CDM son congruentes porque comparten lados iguales. De igual forma, los triángulos ABM y BCM también son congruentes.
  
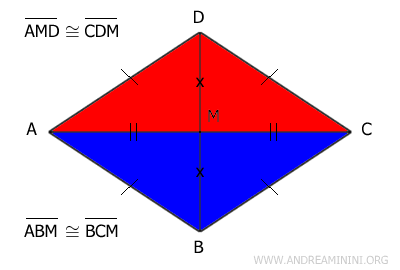
  Además, los triángulos AMD y ABM son congruentes, ya que tienen los tres lados iguales. Por la propiedad transitiva, se concluye que los cuatro triángulos rectángulos en los que quedan divididas las diagonales son congruentes: AMD≅ABM≅BCM≅CDM.
  

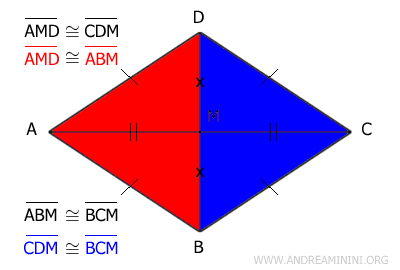
Y así sucesivamente.