Área de un Rombo

El área de un rombo se calcula multiplicando las longitudes de sus diagonales y dividiendo el producto entre dos: $$ A = \frac{d_1 \cdot d_2}{2} $$

Esta fórmula se basa en que el área de un rombo equivale a la de un triángulo rectángulo cuya base y altura corresponden a las diagonales del rombo.

Fórmulas Inversas

Dado que el área de un rombo se expresa como

$$ A = \frac{d_1 \cdot d_2}{2} $$

es posible despejar la longitud de una diagonal multiplicando el área por dos y dividiéndola entre la longitud de la otra diagonal:

$$ d_1 = \frac{2A}{d_2} $$

$$ d_2 = \frac{2A}{d_1} $$

Ejemplo Práctico

Supongamos que tenemos un rombo cuyas diagonales miden d₁ = 3 cm y d₂ = 4 cm. Para calcular su área, aplicamos la fórmula:

$$ A = \frac{d_1 \cdot d_2}{2} $$

Sustituyendo los valores conocidos:

$$ A = \frac{3 \ cm \times 4 \ cm}{2} $$

$$ A = \frac{12 \ cm^2}{2} $$

$$ A = 6 \ cm^2 $$

Por lo tanto, el área del rombo es de 6 cm².

Demostración

Consideremos un rombo ABCD.

Se trazan rectas por los vértices, perpendiculares a las diagonales.

Estas rectas, al ser paralelas entre sí, forman un rectángulo denominado EFGI.

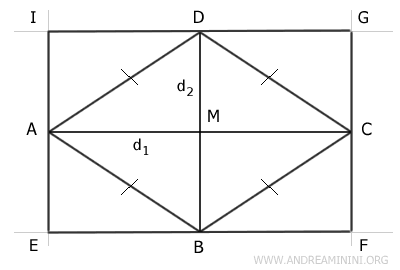
Los lados de dicho rectángulo son congruentes con las diagonales del rombo.

$$ d_1 = \overline{AC} \cong \overline{EF} \cong \overline{GI} $$

$$ d_2 = \overline{BD} \cong \overline{EI} \cong \overline{FG} $$

El área del rectángulo queda dividida en 8 triángulos congruentes, mientras que el área del rombo se reparte en 4 triángulos congruentes.

Por tanto, para hallar el área del rombo basta con calcular el área del rectángulo (base por altura) y dividirla entre dos.

Dicho de otro modo, el área del rombo equivale exactamente a la mitad del área del rectángulo.

$$ A = \frac{b \cdot h}{2} $$

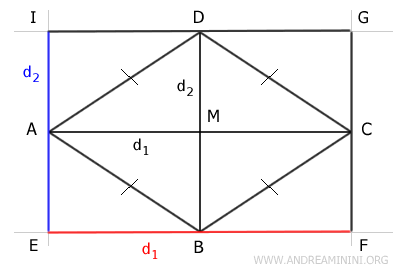
Como los lados del rectángulo coinciden en longitud con las diagonales del rombo, donde b = d₁ y h = d₂, se deduce que basta multiplicar las diagonales del rombo y dividir entre dos.

$$ A = \frac{d_1 \cdot d_2}{2} $$

Esto explica la razón de la fórmula que utilizamos para calcular el área de un rombo.

Observaciones

A continuación, algunas consideraciones sobre el área de un rombo:

• Un rombo es un paralelogramo cuyos lados son congruentes. Por tanto, también es posible calcular su área empleando la fórmula general del paralelogramo: base por altura dividido entre dos. $$ A = \frac{b \cdot h}{2} $$
• El cuadrado es un caso particular de rombo en el que sus diagonales son iguales. Por tanto, se puede calcular el área de un cuadrado utilizando la fórmula del rombo: $$ A = \frac{d \cdot d}{2} = \frac{d^2}{2} $$ De ahí se puede despejar la longitud de la diagonal del cuadrado mediante $$ d^2 = 2A $$ Extrayendo la raíz cuadrada en ambos miembros, se obtiene: $$ \sqrt{d^2} = \sqrt{2A} $$ Por lo tanto, $$ d = \sqrt{2A} $$

Y así sucesivamente.