Cuadrado

Un cuadrado es un paralelogramo que posee cuatro lados iguales y cuatro ángulos rectos.

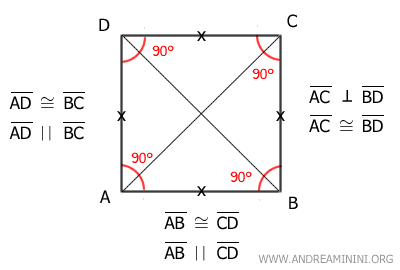
Otra manera de definir un cuadrado es describirlo como un paralelogramo cuyos lados y ángulos son todos iguales. Por eso, un cuadrado es, al mismo tiempo, un rombo y un rectángulo.

Un cuadrado reúne todas las propiedades de un rombo:

• Todos sus lados son congruentes
• Sus diagonales se cruzan perpendicularmente formando un ángulo de 90°
• Sus diagonales dividen por la mitad los ángulos interiores

También comparte todas las propiedades de un rectángulo:

• Cada ángulo interno mide 90°
• Sus diagonales son congruentes, es decir, miden lo mismo

Fórmulas

Principales fórmulas relacionadas con el cuadrado

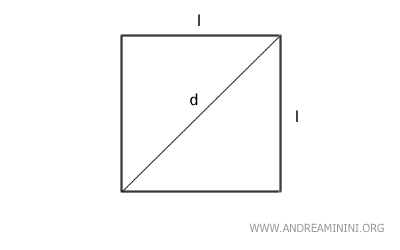
• Perímetro
  El perímetro de un cuadrado se obtiene multiplicando la longitud de uno de sus lados (l) por cuatro: $$ P = 4 \cdot l = l + l + l + l $$
• Área
  El área de un cuadrado es igual al cuadrado de la longitud de su lado (l²): $$ A = l^2 $$ Otra forma de calcularla es elevando la diagonal (d) al cuadrado y dividiéndola entre dos: $$ A=\frac{d^2}{2} $$
• Diagonal
  La diagonal de un cuadrado se calcula multiplicando el lado por la raíz cuadrada de 2: $$ d = l \cdot \sqrt{2} $$

  Nota: Esta fórmula se deduce del teorema de Pitágoras. La diagonal corresponde a la hipotenusa de un triángulo rectángulo cuyos catetos son dos lados del cuadrado: $$ d = \sqrt{l^2+l^2} $$ $$ d = \sqrt{2 \cdot l^2} $$ Al simplificar, se obtiene la fórmula final: $$ d = l \cdot \sqrt{2} $$
  

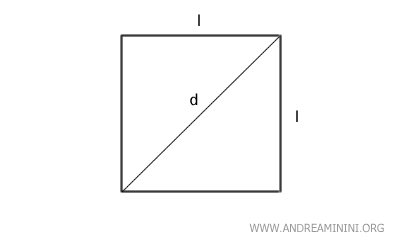
• Lado
  La longitud del lado de un cuadrado se puede hallar dividiendo su perímetro entre cuatro: $$ l = \frac{p}{4} $$ o sacando la raíz cuadrada del área: $$ l = \sqrt{A} $$ También es posible determinarla a partir de la relación entre el lado y el radio de la circunferencia circunscrita, multiplicando el radio por la raíz cuadrada de dos: $$ l = r \cdot \sqrt{2} $$

  Nota: Esta fórmula también surge del teorema de Pitágoras. Los radios que parten del centro de la circunferencia (O) hacia los extremos de un lado del cuadrado forman un ángulo recto de 90°, generando un triángulo rectángulo cuyos catetos coinciden con el radio, y la hipotenusa corresponde al lado del cuadrado. $$ l = \sqrt{r^2+r^2} $$ $$ l = \sqrt{2r^2} $$ Al simplificar, se obtiene la fórmula deseada: $$ l = r \cdot \sqrt{2} $$
  

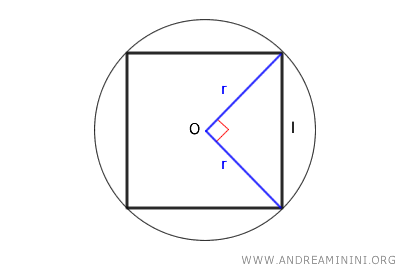
• La longitud del lado de un cuadrado es el doble del radio de su circunferencia inscrita: $$ l = 2r $$

  Nota: Esta relación es bastante intuitiva. El diámetro (2r) de la circunferencia inscrita coincide exactamente con el lado del cuadrado. Esto se debe a que dicho diámetro toca los cuatro lados del cuadrado en puntos de tangencia (uno en cada lado), siendo la mayor circunferencia posible que puede inscribirse en el cuadrado sin sobresalir de sus límites.
  
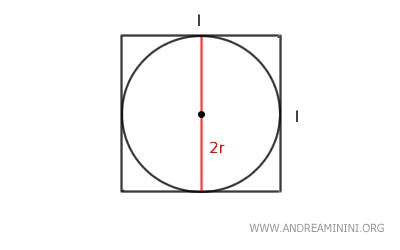
  Además, se puede demostrar que existe una relación entre el radio de la circunferencia inscrita y el lado del cuadrado.

Cómo dibujar un cuadrado

Empieza dibujando el segmento AB, que servirá como primer lado del cuadrado.

Coloca el compás en el punto A y traza un arco con el radio que desees.

Ese arco corta al segmento AB en el punto C.

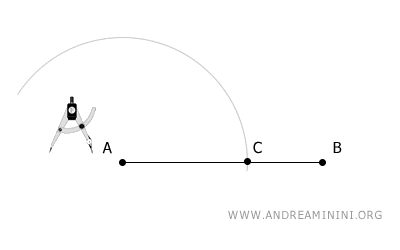
Usando el mismo radio, coloca el compás en el punto C y dibuja otro arco que corte el anterior en el punto D.

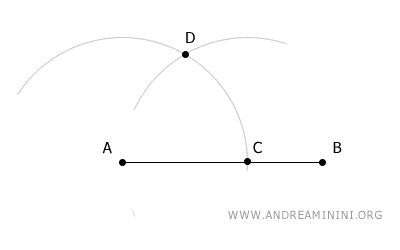
Después, sitúa el compás en el punto D, manteniendo el mismo radio, y dibuja un tercer arco que cruce el primero en el punto E.

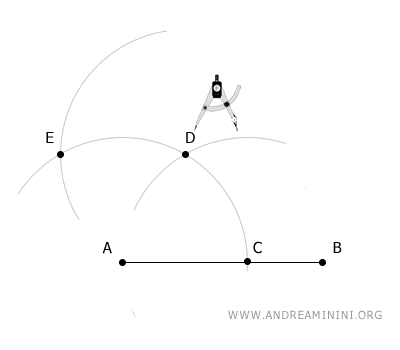
Por último, coloca el compás en el punto E y, con el mismo radio, traza un arco que corte el último arco en el punto F.

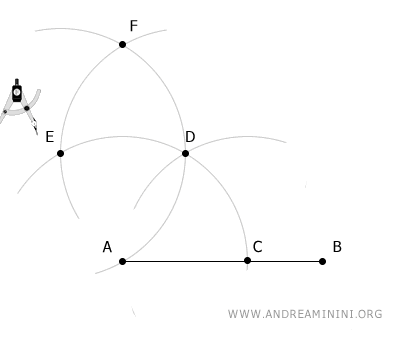
Ahora, dibuja una recta que una los puntos A y F.

Dicha recta es perpendicular a AB y pasa por el punto A.

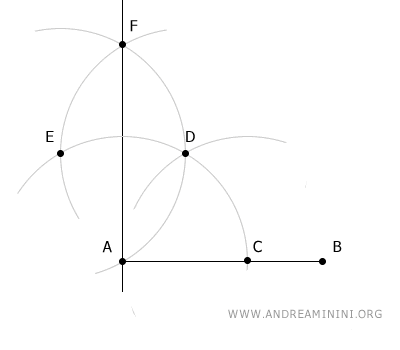
Coloca el compás en A y, con un radio igual al segmento AB, dibuja un arco que corte la recta perpendicular en el punto F.

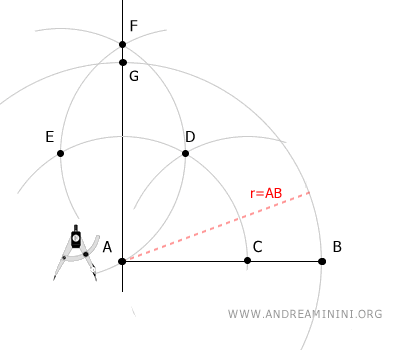
Manteniendo el mismo radio, sitúa el compás en el punto G y traza otro arco.

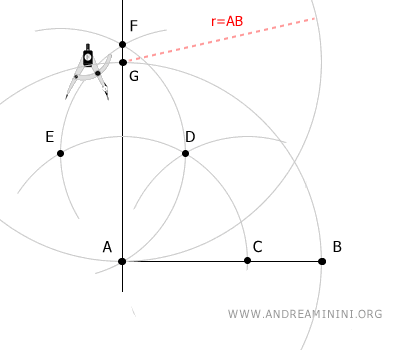
Por último, usando el mismo radio, coloca el compás en el punto B y dibuja un arco que cruce el último arco en el punto H.

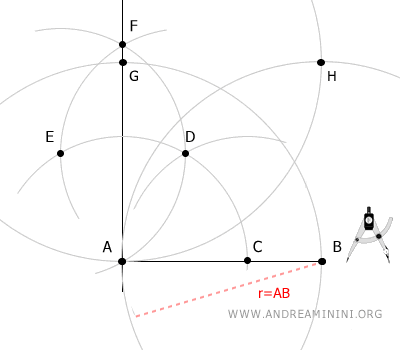
Une con segmentos de recta los puntos A, B, G y H.

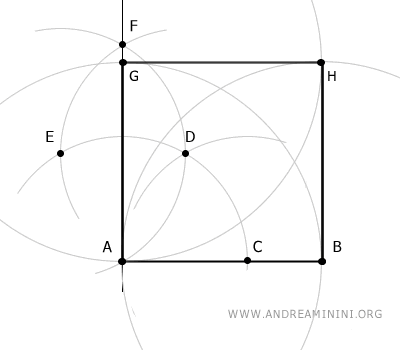
La figura resultante ABHG es un cuadrado.

Otra alternativa es trazar un cuadrado inscrito en una circunferencia.

Observaciones

Algunas observaciones y apuntes interesantes sobre los cuadrados

• Un cuadrado tiene diagonales congruentes

  Demostración: Un cuadrado ABCD, por definición, tiene lados iguales y ángulos rectos. A partir de esta definición, podemos establecer que los triángulos ABD y ABC son congruentes aplicando el criterio lado-ángulo-lado (LAL), ya que comparten el lado AC, tienen lados iguales (AB≅BC) y el ángulo comprendido es congruente (90°), es decir, recto.
  
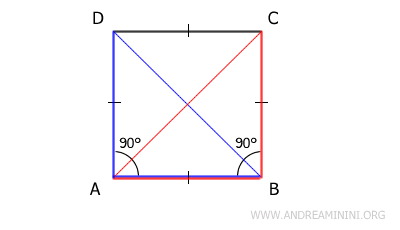
  Dado que los triángulos ABD≅ABC son congruentes, tienen todos sus lados y ángulos correspondientes iguales en el mismo orden. En particular, sus hipotenusas AC y BD son congruentes (AC≅BD), siendo además las diagonales del cuadrado. Por lo tanto, las diagonales de un cuadrado siempre son congruentes.

• Un paralelogramo es un cuadrado si sus diagonales son congruentes y perpendiculares

  Demostración: Sea el paralelogramo ABCD cuyas diagonales AC y BD son congruentes y se cortan perpendicularmente. Estas diagonales se intersectan en su punto medio M, lo que implica que los segmentos AM, BM, CM y DM son iguales.
  
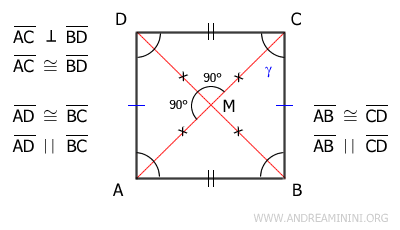
  A partir de ello, podemos afirmar que los triángulos AMD y CDM son congruentes según el criterio lado-ángulo-lado (LAL), pues comparten el lado DM, tienen lados iguales (AM≅CM) y el ángulo comprendido es recto (90°). Por tanto, los triángulos AMD y CDM resultan congruentes en todos sus lados y ángulos.
  
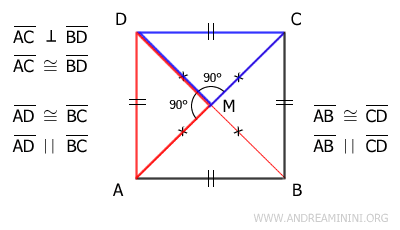
  Lo fundamental aquí es que sus hipotenusas AD y CD también son congruentes, ya que AC y CD corresponden a lados consecutivos del paralelogramo. Si consideramos que en un paralelogramo los lados opuestos son iguales, concluimos que todos los lados del paralelogramo son congruentes. Así, si además sus diagonales son congruentes, podemos asegurar que la figura no es solo un rombo, sino específicamente un cuadrado.

• Una diagonal divide un cuadrado en dos triángulos rectángulos isósceles

  Demostración: Por definición, un cuadrado ABCD tiene lados iguales y ángulos rectos. Una diagonal, como AC, divide el cuadrado en dos triángulos rectángulos, pues necesariamente genera un ángulo de 90°. Además, dichos triángulos son isósceles, ya que tienen dos lados iguales (AB≅BC y AD≅CD), tal como indica la definición inicial.
  
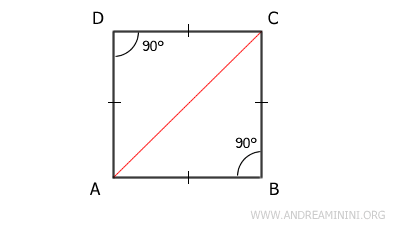
  El mismo razonamiento se aplica a la otra diagonal BD, que también divide el cuadrado en dos triángulos rectángulos isósceles.
  

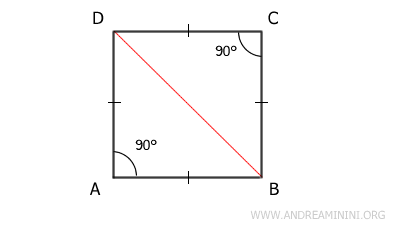
• Las dos diagonales dividen el cuadrado en cuatro triángulos isósceles

  Demostración: El cuadrado ABCD es un paralelogramo cuyos lados y ángulos son iguales. En cualquier paralelogramo, las diagonales se cruzan en su punto medio M.
  
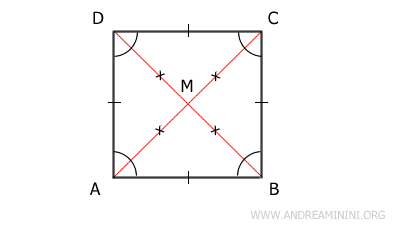
  Sin embargo, a diferencia de otros paralelogramos, en el cuadrado las diagonales también son congruentes. Esto permite dividir el cuadrado en cuatro triángulos que tienen dos lados iguales, es decir, en cuatro triángulos isósceles: ABM, BCM, CDM y ADM. Además, como las diagonales son perpendiculares entre sí, estos cuatro triángulos no solo son isósceles, sino también rectángulos.

• Un paralelogramo es un cuadrado si sus diagonales son congruentes y una de ellas biseca un ángulo

  Demostración: En el paralelogramo ABCD, supongamos que las diagonales AC y BD son congruentes y que una de ellas biseca un ángulo. Por ejemplo, la diagonal AC divide el ángulo en el vértice A en dos ángulos iguales (α'≅α'').
  
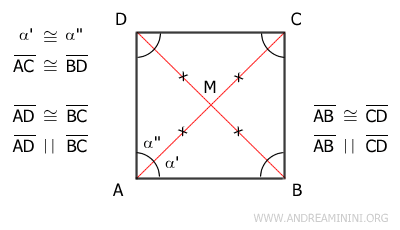
  Como se trata de un paralelogramo, sus lados opuestos son congruentes (AB≅CD y AD≅BC) y paralelos (AB||CD y AD||BC). En este contexto, la diagonal AC actúa como una transversal que corta a las rectas paralelas AD y BC. Por lo tanto, según el teorema de las rectas paralelas, los ángulos alternos internos α''≅γ son congruentes.
  
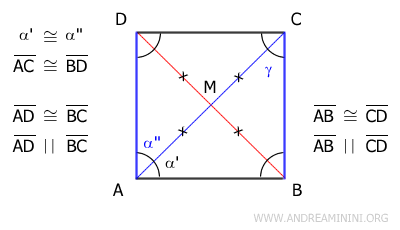
  Dado que α'≅α'' por hipótesis, también podemos deducir que α'≅γ. Esto implica que el triángulo ABC es un triángulo isósceles, pues presenta dos ángulos iguales en la base AC. Al ser isósceles, sus lados AB y BC son congruentes. Por tanto, al tratarse de lados consecutivos del paralelogramo, podemos concluir que todos los lados del paralelogramo son congruentes.
  
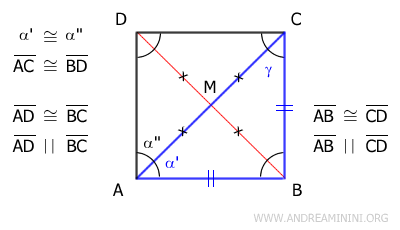
  El paso final es determinar si el paralelogramo es un rombo o un cuadrado. La clave está en que sus diagonales son congruentes, lo que confirma que la figura ABCD es, en efecto, un cuadrado.

Y así sucesivamente.