Relación Entre el Lado de un Cuadrado y el Radio de su Circunferencia Inscrita
El lado de un cuadrado equivale al doble del radio (o, lo que es lo mismo, al diámetro) de su circunferencia inscrita. $$ l = 2r $$ 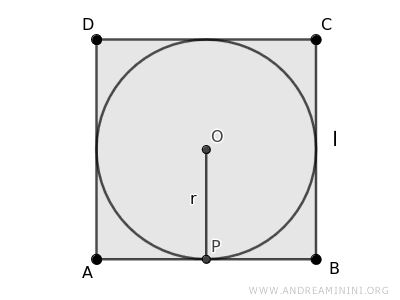
Como corolario, se deduce que el radio de la circunferencia inscrita es exactamente la mitad de la longitud del lado del cuadrado.
$$ r = \frac{l}{2} $$
Aunque pueda parecer evidente, conviene enunciarlo de forma explícita.
La demostración de que el diámetro de la circunferencia inscrita en un cuadrado es congruente con la longitud de su lado es bastante sencilla, ya que se fundamenta en principios geométricos básicos.
Demostración
Consideremos un cuadrado ABCD con su circunferencia inscrita.
En un cuadrado, el centro O de la circunferencia inscrita coincide con el centro geométrico del propio cuadrado.
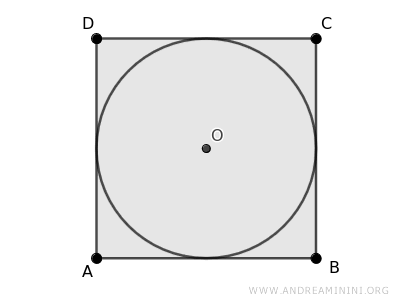
Designemos este punto como \(O\) y llamemos \(r\) al radio de la circunferencia.
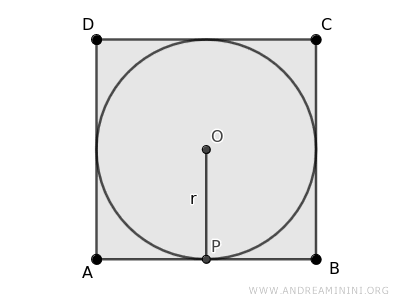
La circunferencia inscrita toca cada lado del cuadrado en un único punto de tangencia, que llamaremos \(P\), \(Q\), \(R\) y \(S\).
Estos puntos de tangencia determinan que los radios OP, OQ, OR y OS sean perpendiculares a los lados del cuadrado, formando ángulos rectos (90°).
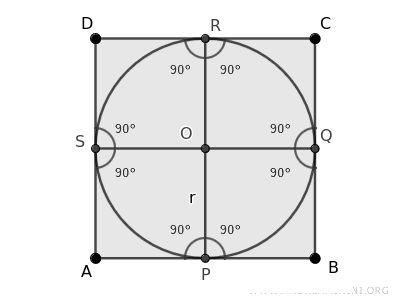
A continuación, trazamos las diagonales del cuadrado.
En cualquier cuadrado, las diagonales son congruentes y se bisecan mutuamente en su punto medio.
El centro O de la circunferencia inscrita se encuentra en el punto de intersección de dichas diagonales, coincidiendo con el centro del cuadrado.
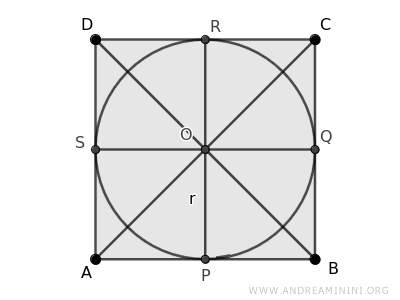
Las diagonales dividen el cuadrado en ocho triángulos: AOP, AOS, BOP, BOQ, COQ, COR, DOR y DOS.
Estos ocho triángulos presentan las siguientes características:
- Son triángulos rectángulos porque los radios OP, OQ, OR y OS son perpendiculares (90°) a los lados del cuadrado.
- Son triángulos isósceles porque tienen dos ángulos congruentes de 45°. Esto implica que sus lados no perpendiculares son iguales.
Nota: El ángulo central en O (360°) se divide en ocho ángulos iguales de 45° cada uno. Además, las diagonales bisecan cada ángulo recto del cuadrado en dos ángulos de 45°.

- Son triángulos congruentes, ya que, según el primer criterio de congruencia de triángulos, poseen lados no perpendiculares congruentes (el radio y la mitad del lado del cuadrado) y un ángulo recto congruente (90°).
Dado que los ocho triángulos son congruentes, basta analizar uno de ellos, por ejemplo, el triángulo AOP.

En resumen, el triángulo AOP es isósceles, por lo que sus lados no perpendiculares AP ≅ OP son congruentes.
$$ \overline{AP} = \overline{OP} $$
El segmento OP corresponde al radio de la circunferencia inscrita.
$$ \overline{OP} = r $$
El segmento AP es la mitad del lado L del cuadrado.
$$ \frac{L}{2} = r $$
Multiplicando ambos miembros de la ecuación por dos, obtenemos:
$$ \frac{L}{2} \cdot 2 = r \cdot 2 $$
$$ L = 2r $$
Queda así demostrado que el diámetro de la circunferencia inscrita \(2r\) coincide exactamente con la longitud del lado del cuadrado \(L\).
Y así sucesivamente.