Área de un Polígono Circunscrito a una Circunferencia

El área de un polígono circunscrito a una circunferencia se calcula multiplicando el semiperímetro (p) del polígono por el radio (r) de la circunferencia. $$ A = p \cdot r $$ Aquí, el semiperímetro (p) es la mitad del perímetro (P) del polígono, es decir, p = P/2.

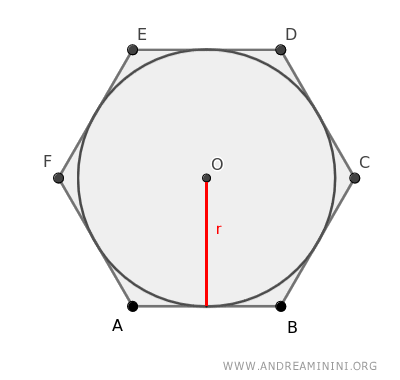
Dicho de forma sencilla, el área de un polígono circunscrito a una circunferencia se obtiene multiplicando el perímetro por el radio de la circunferencia inscrita y dividiendo el resultado entre dos.

$$ A = \frac{P \cdot r}{2} $$

Si expresamos el perímetro como el doble del semiperímetro, es decir, P = 2p, y simplificamos, llegamos nuevamente a la fórmula original.

$$ A = \frac{2p \cdot r}{2} $$

$$ A = p \cdot r $$

Esta fórmula permite calcular el área (A) del polígono conociendo el radio (r) de la circunferencia y el semiperímetro del polígono.

Nota: En un polígono regular, el radio de la circunferencia se denomina también apotema o radio interior.

Explicación

Analicemos el caso de un polígono circunscrito a una circunferencia.

Consideremos, por ejemplo, un hexágono.

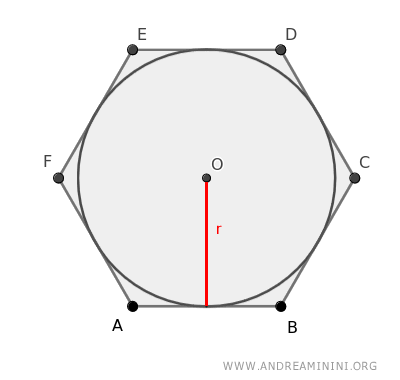
Podemos dividir el hexágono en 6 triángulos, cada uno de ellos con un lado (l) del polígono como base y el radio (r) de la circunferencia como altura.

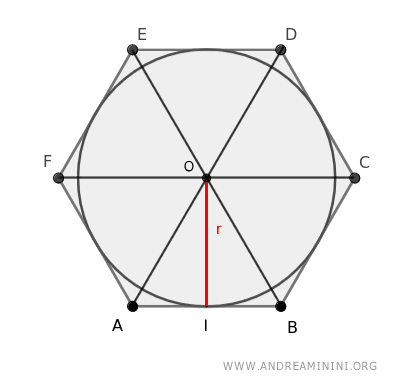
El área de cada triángulo se calcula multiplicando la base por la altura y dividiendo entre dos; en este caso, equivale a la longitud del lado por el radio, dividido por 2.

$$ \frac{l \cdot r}{2} $$

Por lo tanto, el área del polígono es igual a la suma de las áreas de esos triángulos.

$$ A = \frac{ \overline{AB} \cdot r }{2} + \frac{ \overline{BC} \cdot r }{2} + \frac{ \overline{CD} \cdot r }{2} + \frac{ \overline{DE} \cdot r }{2} + \frac{ \overline{EF} \cdot r }{2} + \frac{ \overline{FA} \cdot r }{2} $$

$$ A = \frac{ ( \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EF} + \overline{FA} ) \cdot r }{2} $$

La suma del numerador corresponde al perímetro P del polígono, de modo que obtenemos:

$$ A = \frac{ P \cdot r }{2} $$

Si expresamos el perímetro como el doble del semiperímetro, P = 2p, y simplificamos, obtenemos:

$$ A = \frac{ 2p \cdot r }{2} $$

Lo que se simplifica finalmente en:

$$ A = p \cdot r $$

Así llegamos de nuevo a la fórmula que pretendíamos demostrar.

Demostración Geométrica: Si consideramos el perímetro como un cateto de un triángulo rectángulo y el radio como el otro, el área de dicho triángulo equivale al área del polígono.

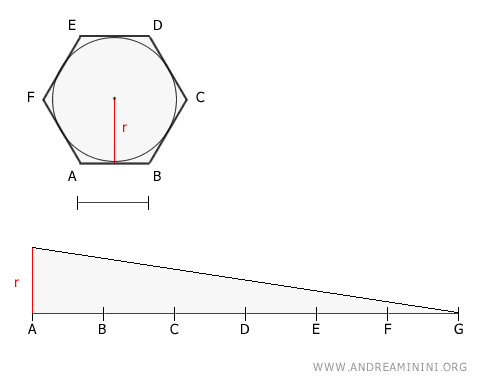
Notas Adicionales

Algunas observaciones adicionales:

• Fórmulas Inversas
  La fórmula del área de un polígono circunscrito, $$ A = p \cdot r $$, permite deducir fórmulas inversas muy útiles. Por ejemplo, si conocemos el área (A) y el semiperímetro (p), podemos calcular el radio: $$ r = \frac{A}{p} $$. De forma similar, si conocemos el área (A) y el radio (r), podemos hallar el semiperímetro: $$ p = \frac{A}{r} $$.

Y así sucesivamente.