Diagonal de un Cuadrado

La longitud de la diagonal de un cuadrado (d) se obtiene multiplicando la longitud de uno de sus lados (l) por la raíz cuadrada de 2: $$ d = l \cdot \sqrt{2} $$

La relación entre la diagonal y el lado es constante en todos los cuadrados, sin importar su tamaño.

$$ \frac{d}{l} = \sqrt{2} $$

Gracias a esta relación, es sencillo calcular la diagonal si se conoce la longitud del lado, o determinar el lado si se conoce la diagonal.

Ejemplo

Veamos un ejemplo con un cuadrado cuyo lado mide 4.

$$ l = 4 $$

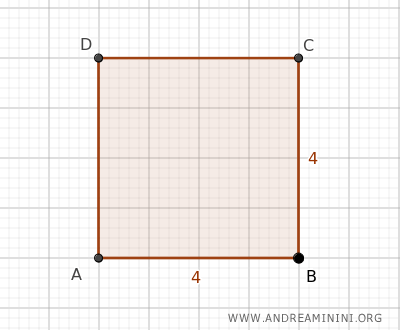
La longitud de su diagonal es:

$$ d = l \cdot \sqrt{2} $$

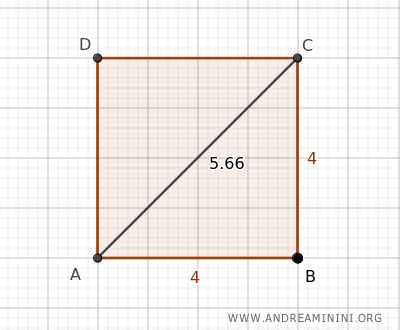
$$ d = 4 \cdot \sqrt{2} $$

$$ d = 5.66 $$

Por lo tanto, la diagonal del cuadrado mide aproximadamente 5.66 unidades.

Demostración

Este resultado puede demostrarse aplicando el teorema de Pitágoras.

La diagonal divide el cuadrado en dos triángulos rectángulos isósceles.

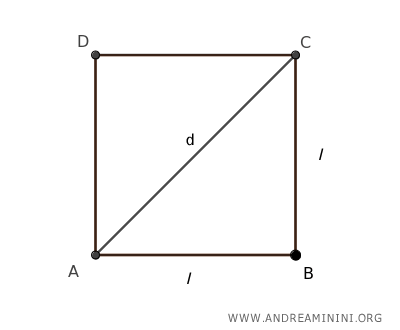
En cada uno de estos triángulos, los catetos corresponden a los lados del cuadrado (l), y la hipotenusa es la diagonal (d).

El teorema de Pitágoras establece que, en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los catetos.

$$ d^2 = l^2 + l^2 $$

Al simplificar, se obtiene:

$$ d^2 = 2 \cdot l^2 $$

Tomando la raíz cuadrada en ambos miembros y simplificando, se llega a:

$$ \sqrt{ d^2 } = \sqrt{ 2 \cdot l^2 } $$

$$ d = l \cdot \sqrt{2} $$

Y así se deduce la fórmula que queríamos demostrar.

Observaciones

A continuación, algunas notas y observaciones adicionales sobre la diagonal de un cuadrado:

• La diagonal y el lado de un cuadrado son inconmensurables
  La diagonal y el lado de un cuadrado son inconmensurables, lo que significa que no tienen un divisor común que permita medirlas exactamente con la misma unidad de longitud.

  Demostración. Consideremos el cuadrado ABCD.
  
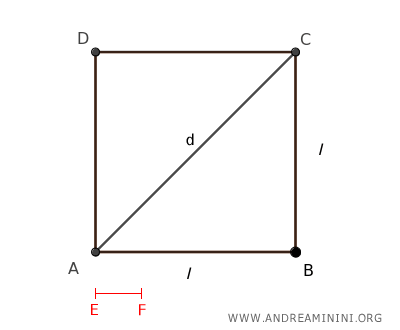
  Supongamos, solo a modo de argumento, que el lado AB y la diagonal AC fueran conmensurables. Esto implicaría la existencia de una unidad común EF, que encajaría exactamente un número entero de veces tanto en la diagonal AC como en el lado AB. Es decir: $$ \overline{AC} = m \cdot \overline{EF} $$ $$ \overline{AB} = n \cdot \overline{EF} $$ Según el teorema de Pitágoras, en el triángulo rectángulo ABC, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos: $$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 $$ Como en un cuadrado todos los lados son iguales, se cumple que AB = BC: $$ \overline{AC}^2 = \overline{AB}^2 + \overline{AB}^2 $$ $$ \overline{AC}^2 = 2 \cdot \overline{AB}^2 $$ Sustituyendo AC = m · EF y AB = n · EF, obtenemos: $$ (m \cdot \overline{EF})^2 = 2 \cdot (n \cdot \overline{EF})^2 $$ $$ m^2 \cdot \overline{EF}^2 = 2 \cdot n^2 \cdot \overline{EF}^2 $$ Simplificando, eliminamos $\overline{EF}^2$ en ambos lados: $$ m^2 = 2 \cdot n^2 $$ Aquí, m y n serían números enteros. Sin embargo, esta ecuación no tiene solución en enteros positivos, pues el lado izquierdo y el derecho tendrían que descomponerse en los mismos factores primos, y el lado derecho tiene un factor extra de 2. Por tanto, no existe ningún par de enteros positivos (m, n) que cumpla m² = 2n². Como esto lleva a una contradicción, nuestra suposición inicial de que la diagonal y el lado son conmensurables es falsa. En consecuencia, la diagonal y el lado de un cuadrado son, en efecto, inconmensurables.

Y así sucesivamente.