Relación Entre el Lado de un Cuadrado y el Radio de su Circunferencia Circunscrita
Existe una relación directa entre la longitud del lado de un cuadrado y el radio de la circunferencia circunscrita que pasa por todos sus vértices:
- La longitud del lado del cuadrado es igual al radio de la circunferencia circunscrita multiplicado por la raíz cuadrada de dos. $$ l = r \cdot \sqrt{2} $$
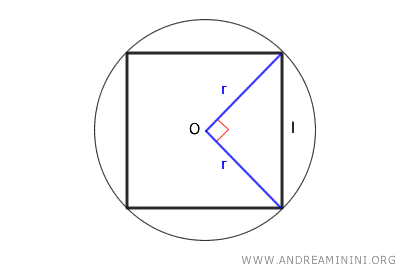
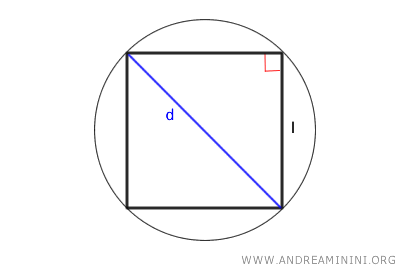
- La longitud del lado también puede expresarse como el doble del radio (2r) de la circunferencia circunscrita (que coincide con la diagonal del cuadrado), dividido entre la raíz cuadrada de dos. $$ l = \frac{2r}{\sqrt{2}} = \frac{d}{\sqrt{2}} $$
Un Ejemplo Práctico
En este ejemplo, el cuadrado tiene un lado de longitud 3, y el radio de la circunferencia circunscrita es r = 2.1213.
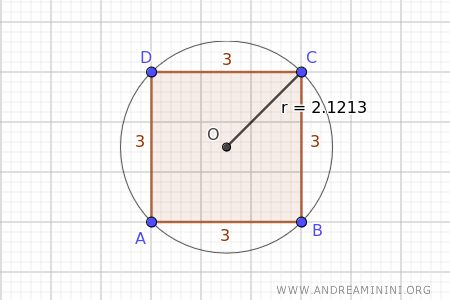
Comprobemos la relación entre el lado del cuadrado y el radio de su circunferencia circunscrita utilizando la primera fórmula:
$$ l = r \cdot \sqrt{2} $$
$$ 3 = 2.1213 \cdot \sqrt{2} = 3 $$
La igualdad se verifica correctamente.
Ahora, verifiquemos la misma relación empleando la segunda fórmula:
$$ l = \frac{2r}{\sqrt{2}} $$
$$ l = \frac{2 \cdot 2.1213}{\sqrt{2}} = 3 $$
De nuevo, la igualdad se cumple.
Demostración
Podemos dividir la demostración en dos partes, cada una correspondiente a una de las fórmulas.
1] Primera Fórmula
Consideremos un cuadrado inscrito en su circunferencia circunscrita.
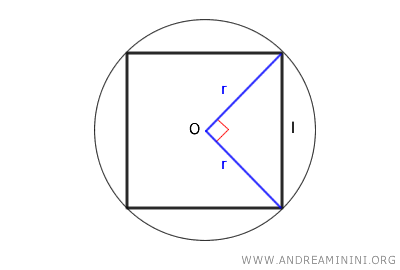
Los radios que van del centro (O) a los extremos de un lado del cuadrado forman un triángulo rectángulo, donde el lado del cuadrado es la hipotenusa y los radios son los catetos.
Aplicando el teorema de Pitágoras, se puede calcular la hipotenusa a partir de la longitud de los catetos:
$$ l = \sqrt{r^2 + r^2} $$
$$ l = \sqrt{2r^2} $$
$$ l = r \cdot \sqrt{2} $$
Así queda demostrada la primera fórmula.
2] Segunda Fórmula
La diagonal de un cuadrado se obtiene multiplicando la longitud del lado por la raíz cuadrada de dos:
$$ d = l \cdot \sqrt{2} $$
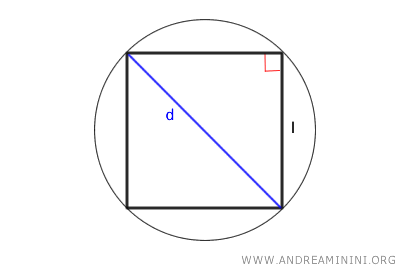
Como la diagonal es igual al doble del radio, es decir, d = 2r, podemos deducir la longitud del lado a partir del radio:
$$ 2r = l \cdot \sqrt{2} $$
Por lo tanto, la longitud del lado (l) del cuadrado es igual al radio (r) de la circunferencia circunscrita multiplicado por dos y dividido entre la raíz cuadrada de dos:
$$ l = \frac{2r}{\sqrt{2}} $$
Demostración Alternativa. Esta fórmula también se puede deducir de manera sencilla a partir de una manipulación algebraica de la primera relación. Partiendo de $$ l = r \cdot \sqrt{2} $$ podemos multiplicar y dividir por la raíz cuadrada de dos: $$ l = r \cdot \sqrt{2} \cdot \frac{\sqrt{2}}{\sqrt{2}} $$ Lo que se simplifica a: $$ l = \frac{r \cdot \sqrt{2} \cdot \sqrt{2}}{\sqrt{2}} $$ $$ l = \frac{r \cdot 2}{\sqrt{2}} $$
Y así sucesivamente.