Área de un Paralelogramo
La fórmula para calcular el área de un paralelogramo es: $$ A = b \times h $$ donde \( A \) es el área, \( b \) representa la longitud de la base y \( h \) es la altura, que corresponde a la distancia perpendicular entre la base y el lado opuesto.
El estudio del área del paralelogramo se remonta a la Antigua Grecia, cuando matemáticos como Euclides describieron diversas propiedades de estas y otras figuras geométricas en su célebre obra, "Elementos".
Un Ejemplo Práctico
Consideremos un paralelogramo cuya base mide 5 metros y cuya altura es de 3 metros.
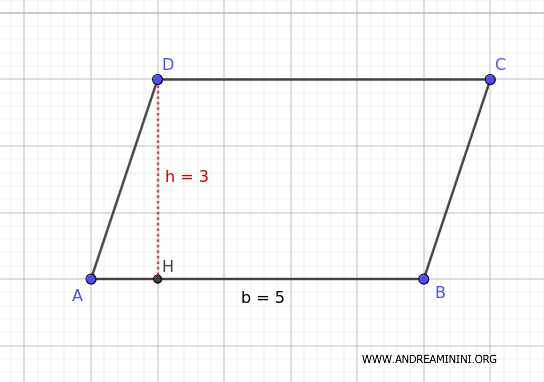
El área del paralelogramo es:
$$ A = 5 \, m \times 3 \, m = 15 \, m^2 $$
Explicación
Para comprender cómo se deduce esta fórmula, imagina transformar el paralelogramo en un rectángulo.
Dibuja la altura en el interior del paralelogramo, partiendo desde el vértice D.
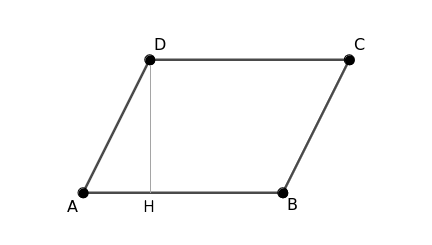
Después, corta el triángulo ADH y trasládalo al lado opuesto.
De este modo se obtiene el rectángulo HDCE, que conserva la misma base y altura que el paralelogramo original.
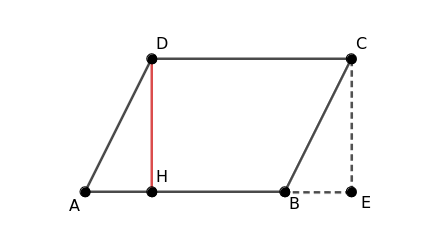
Así, un paralelogramo es equivalente a un rectángulo con la misma base y altura.
Y como el área de un rectángulo se obtiene multiplicando la base por la altura, este mismo razonamiento se aplica al paralelogramo.
Cálculo del Área Usando Coordenadas Cartesianas
Otra forma de calcular el área de un paralelogramo consiste en emplear las coordenadas cartesianas de sus vértices.
Si los vértices del paralelogramo están definidos por los puntos \( (x_1, y_1) \), \( (x_2, y_2) \), \( (x_3, y_3) \) y \( (x_4, y_4) \), el área se puede determinar mediante el determinante de sus coordenadas:
$$ A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right| $$
Ejemplo
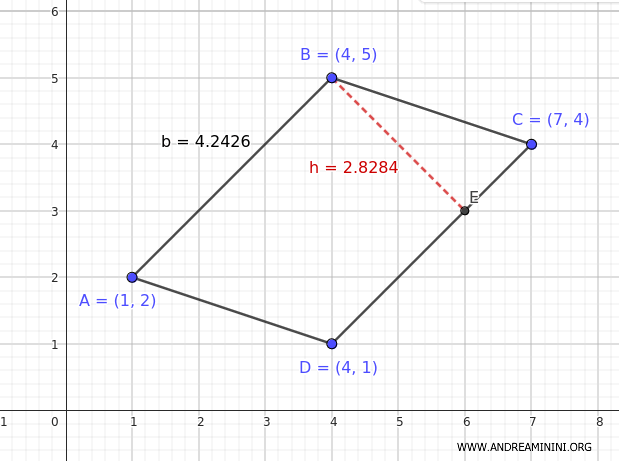
Veamos un ejemplo de cómo calcular el área de un paralelogramo a partir de las coordenadas de sus vértices.
Supongamos que tenemos un paralelogramo cuyos vértices se encuentran en las siguientes coordenadas:
$$ A (1, 2) $$
$$ B (4, 5) $$
$$ C (7, 4) $$
$$ D (4, 1) $$
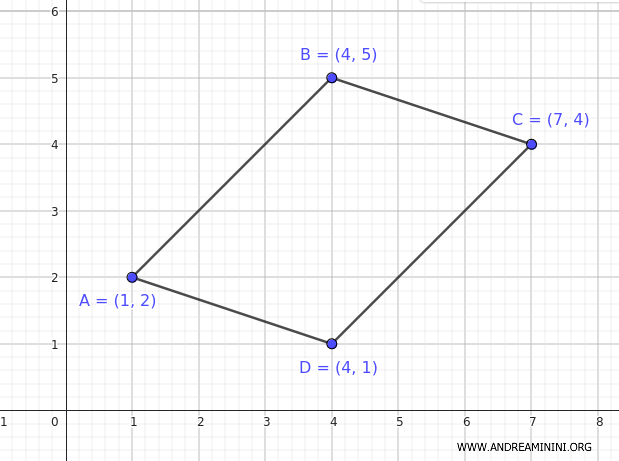
Escribimos las coordenadas en orden cíclico:
$$ (x_1, y_1) = (1, 2) \\
(x_2, y_2) = (4, 5) \\
(x_3, y_3) = (7, 4) \\
(x_4, y_4) = (4, 1) $$
Aplicamos la fórmula del determinante:
$$ A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right| $$
Sustituyendo los valores numéricos:
$$ A = \frac{1}{2} \left| 1 \cdot 5 + 4 \cdot 4 + 7 \cdot 1 + 4 \cdot 2 - (2 \cdot 4 + 5 \cdot 7 + 4 \cdot 4 + 1 \cdot 1) \right| $$
Calculamos los productos uno por uno:
$$ A = \frac{1}{2} \left| 5 + 16 + 7 + 8 - (8 + 35 + 16 + 1) \right| $$
$$ A = \frac{1}{2} \left| 36 - 60 \right| $$
$$ A = \frac{1}{2} \left| -24 \right| $$
$$ A = \frac{1}{2} \cdot 24 $$
$$ A = 12 $$
Por lo tanto, el área del paralelogramo con vértices en las coordenadas \( (1, 2) \), \( (4, 5) \), \( (7, 4) \) y \( (4, 1) \) es \( 12 \, \text{unidades cuadradas} \).
De hecho, si calculamos el área del paralelogramo usando la fórmula \( A = b \cdot h \), también obtenemos \( A = 12 \).
$$ A = b \cdot h = 4.2426 \cdot 2.8284 = 12 $$
Y así sucesivamente.