Teorema de equivalencia entre un triángulo y un trapecio
Un trapecio es equivalente a un triángulo que tiene la misma altura (h) y una base igual a la suma de las dos bases (B + b) del trapecio.
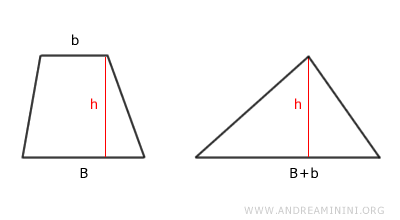
En otras palabras: un triángulo y un trapecio tienen la misma área si se cumplen las siguientes condiciones:
- las alturas son iguales
- la base del triángulo es igual a la suma de las bases del trapecio
En este caso, son polígonos equivalentes.
Se dice que dos polígonos son equivalentes cuando no se superponen y cubren exactamente la misma superficie.
Un ejemplo práctico
En este ejemplo, tenemos un triángulo y un trapecio con altura común h = 4.
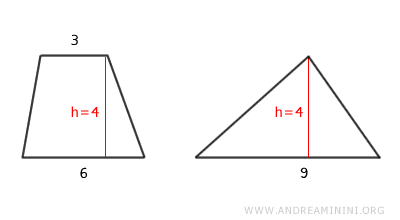
La base del triángulo es 9, que coincide con la suma de las bases del trapecio (6 + 3), por lo que se puede aplicar directamente el teorema de equivalencia.
El área del triángulo es la mitad del producto de su base por su altura:
$$ A_t = \frac{b \cdot h}{2} = \frac{9 \cdot 4}{2} = \frac{36}{2} = 18 $$
Al ser polígonos equivalentes, el trapecio tendrá la misma área:
$$ A_z = 18 $$
Por tanto, no es necesario realizar más cálculos.
Si queremos comprobarlo, podemos calcular el área del trapecio con su fórmula: el área es la mitad del producto de la suma de las bases por la altura. $$ A_z = \frac{(B_z + b_z) \cdot h}{2} = \frac{(6 + 3) \cdot 4}{2} = \frac{9 \cdot 4}{2} = \frac{36}{2} = 18 $$ El resultado es el mismo.
Demostración
Consideremos un triángulo y un trapecio:
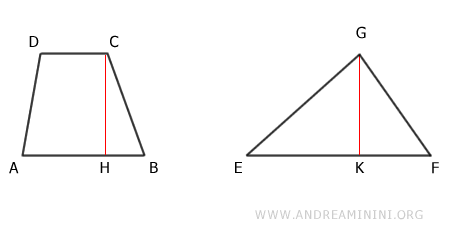
Inicialmente, ambas figuras tienen la misma altura:
$$ \overline{CH} \cong \overline{GK} $$
Además, la suma de las bases AB y CD del trapecio es igual a la base EF del triángulo:
$$ \overline{AB} + \overline{CD} \cong \overline{EF} $$
Debemos demostrar que son equivalentes, es decir, que tienen la misma área.
Para ello, prolongamos la base mayor AB del trapecio con un segmento BL, cuya longitud es igual a la base menor CD:
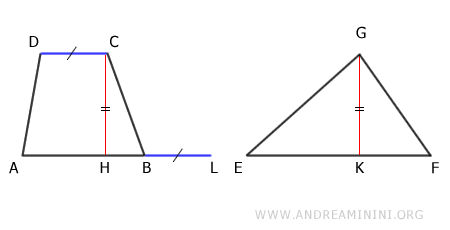
A continuación, trazamos el segmento DL entre los puntos D y L:
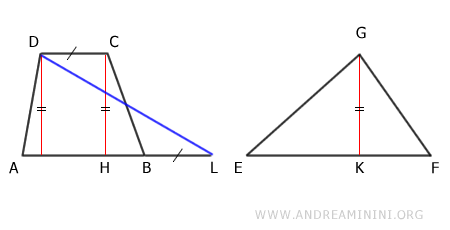
El segmento AL es igual a la base EF del triángulo porque:
- BL ≅ CD por construcción
- AB + CD ≅ EF por hipótesis inicial, de modo que AB + BL ≅ EF
Por tanto:
$$ \overline{AL} \cong \overline{EF} $$
Según el criterio de congruencia de triángulos, el triángulo ADL es equivalente al triángulo EFG, ya que tienen la misma altura CH ≅ GK y la misma base AL ≅ EF:
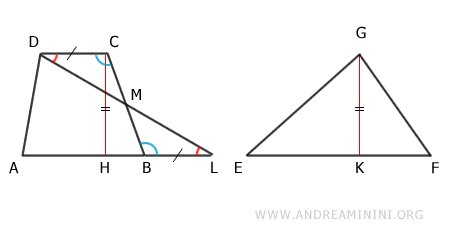
Por otro lado, los triángulos MCD y MBL son también congruentes porque:
- Las bases del trapecio son paralelas (AB || CD), y AL es una prolongación de AB.
- BL ≅ CD por construcción.
- Los ángulos adyacentes en BL y CD son iguales, por el teorema de las paralelas (ángulos alternos internos).
Por tanto:
$$ MCD \cong MBL $$
Al ser congruentes, son también equivalentes en área:
$$ MCD \doteq MBL $$
Podemos entonces considerar el trapecio ABCD como la suma del cuadrilátero ABMD y el triángulo MCD:
$$ ABCD \doteq ABMD + MCD $$
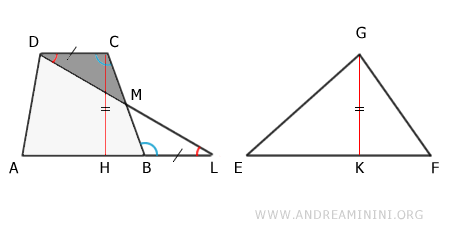
De igual modo, el triángulo ADL se descompone en ABMD más el triángulo MBL:
$$ ADL \doteq ABMD + MBL $$
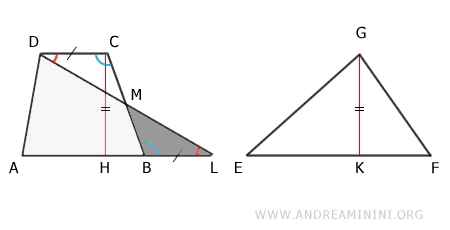
Como MCD y MBL son equivalentes, se concluye que:
$$ ABCD \doteq ABMD + MCD \doteq ABMD + MBL \doteq ADL $$
Por tanto, el trapecio ABCD y el triángulo ADL son polígonos equivalentes:
$$ ABCD \doteq ADL $$
Por último, como el triángulo ADL es equivalente al triángulo EFG, se deduce:
$$ ABCD \doteq ADL \doteq EFG $$
$$ ABCD \doteq EFG $$
Así queda demostrada la proposición inicial.
Demostración alternativa
Podemos también justificar este teorema mediante razonamiento algebraico.
El área de un triángulo es:
$$ A_t = \frac{b_t \cdot h_t}{2} $$
El área de un trapecio es:
$$ A_z = \frac{(B_z + b_z) \cdot h_z}{2} $$
Buscamos las condiciones en las que:
$$ A_t = A_z $$
Es decir:
$$ \frac{b_t \cdot h_t}{2} = \frac{(B_z + b_z) \cdot h_z}{2} $$
Si además las alturas son iguales, ht = hz:
$$ \frac{b_t \cdot h_t}{2} = \frac{(B_z + b_z) \cdot h_t}{2} $$
Si además bt = Bz + bz:
$$ \frac{b_t \cdot h_t}{2} = \frac{b_t \cdot h_t}{2} $$
La igualdad es evidente: las áreas son iguales.
Por tanto, el triángulo y el trapecio son equivalentes cuando tienen la misma altura y la base del triángulo es igual a la suma de las bases del trapecio.
Y así sucesivamente.