Teorema de equivalencia entre un paralelogramo y un triángulo
Un triángulo es equivalente a un paralelogramo que tiene la misma altura y una base que es la mitad de la del triángulo.
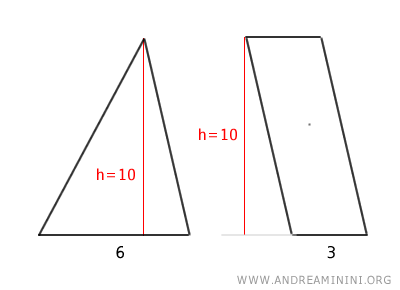
De manera equivalente, un triángulo es equivalente a un paralelogramo que posee la misma base y la mitad de la altura del triángulo.
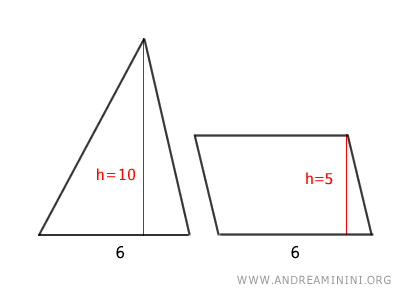
En otras palabras: si un triángulo tiene la misma altura que un paralelogramo y una base que es el doble, las áreas serán iguales.
Del mismo modo, si el triángulo tiene la misma base y el doble de altura que el paralelogramo, las áreas también coincidirán.
Un ejemplo práctico
Consideremos un triángulo y un paralelogramo.
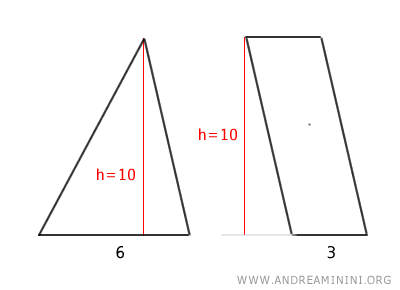
Ambas figuras tienen la misma altura, h = 10.
Además, la base del triángulo mide 6, es decir, el doble de la base del paralelogramo (3).
Por el teorema de equivalencia, ambos polígonos tienen la misma área:
$$ A_p = A_t $$
donde Ap y At son las áreas del paralelogramo y del triángulo, respectivamente.
El área del paralelogramo se calcula multiplicando la base (3) por la altura (10):
$$ A_p = 3 \cdot 10 = 30 $$
Por lo tanto, el área del triángulo también es:
$$ A_t = 30 $$
Para comprobarlo, basta calcular el área del triángulo, que es la mitad del producto de su base (6) por su altura (10):
$$ A_t = \frac{6 \cdot 10}{2} = \frac{60}{2} = 30 $$
El resultado coincide perfectamente.
Ejemplo 2
En este segundo ejemplo, el paralelogramo tiene la misma base que el triángulo (b = 6), pero su altura es la mitad (hp = 5), en comparación con la altura del triángulo (ht = 10).
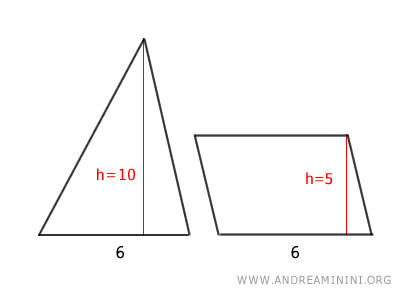
Según el teorema de equivalencia, ambos polígonos son equivalentes, ya que tienen la misma área:
$$ A_p = A_t $$
donde Ap y At son las áreas del paralelogramo y del triángulo, respectivamente.
El área del paralelogramo se obtiene multiplicando su base (6) por su altura (5):
$$ A_p = 6 \cdot 5 = 30 $$
Por lo tanto, el área del triángulo también será:
$$ A_t = 30 $$
El resultado puede comprobarse fácilmente calculando el área del triángulo, como la mitad del producto de su base (6) por su altura (10):
$$ A_t = \frac{6 \cdot 10}{2} = \frac{60}{2} = 30 $$
Como era de esperar, los resultados coinciden.
Demostración
A] Paralelogramo con la misma altura y la mitad de la base del triángulo
Para demostrar el teorema, consideremos un triángulo ABC y un paralelogramo DEFG.
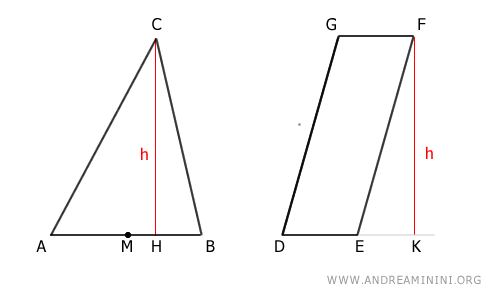
Sea M el punto medio del segmento AB:
$$ \overline{AM} \cong \overline{BM} $$
De partida, las alturas de ambas figuras son congruentes:
$$ \overline{CH} \cong \overline{FK} $$
La base correspondiente del paralelogramo es congruente con la mitad de la base del triángulo.
Dicho de otro modo: la base del triángulo (AB) es el doble que la base del paralelogramo (DE):
$$ \overline{AB} \cong 2 \cdot \overline{DE} $$
o bien:
$$ \overline{AM} \cong \overline{BM} \cong \overline{DE} $$
Debemos probar que el triángulo ABC y el paralelogramo DEFG son equivalentes, es decir, que tienen la misma área.
Para ello, trazamos una recta paralela al lado AC que pase por el punto medio M:
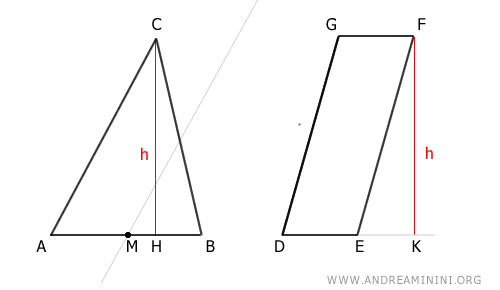
A continuación, trazamos una recta paralela a la base AB que pase por el vértice C:
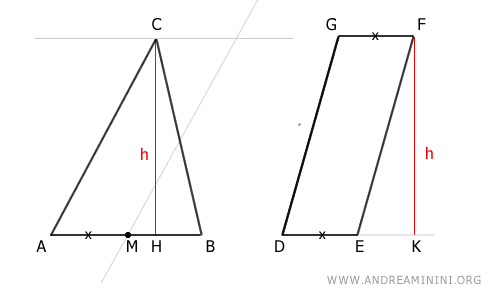
Se forma así el paralelogramo AMNC:
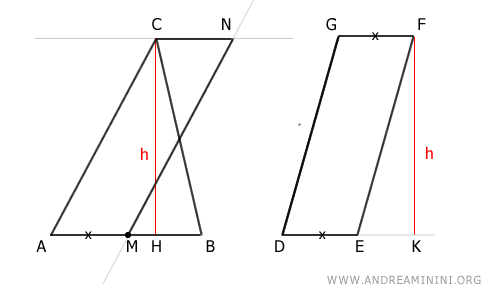
Según el teorema de equivalencia de paralelogramos, AMNC es equivalente a DEFG, ya que poseen la misma base (AM ≅ DE) y la misma altura (CM ≅ FK):
$$ AMNC \cong DEFG $$
Además, los ángulos α ≅ δ y β ≅ γ son congruentes, por tratarse de ángulos alternos internos entre rectas paralelas (teorema de las paralelas):
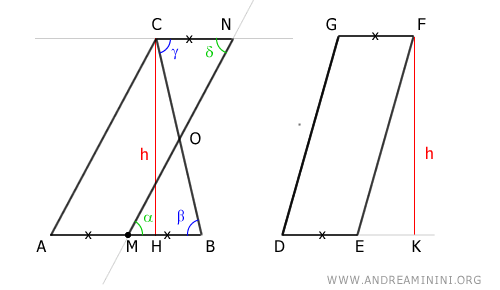
Como BM ≅ AM (por ser M el punto medio), y los lados opuestos del paralelogramo son paralelos, resulta que BM ≅ CN.
Por lo tanto, los triángulos MBO y CNO son congruentes, según el segundo criterio de congruencia de triángulos, ya que tienen un lado congruente BM ≅ CN y ángulos adyacentes congruentes α ≅ δ y β ≅ γ:
$$ MBO \cong CNO $$
Al ser congruentes, estos dos triángulos son también equivalentes en área:
$$ MBO \doteq CNO $$
Representamos las áreas equivalentes MBO y CNO en gris:
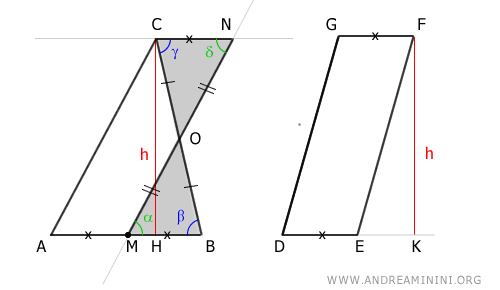
Ahora podemos expresar el triángulo ABC como la suma del trapecio AMOC más el triángulo MBO:
$$ ABC \doteq AMOC + MBO $$
Igualmente, el paralelogramo AMNC es la suma de AMOC más el triángulo CNO:
$$ AMNC \doteq AMOC + CNO $$
Dado que MBO y CNO son equivalentes, concluimos que:
$$ ABC \doteq AMOC + MBO \doteq AMOC + CNO \doteq AMNC $$
$$ ABC \doteq AMNC $$
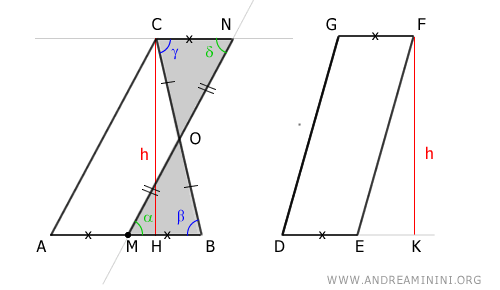
Como AMNC es equivalente a DEFG, deducimos que el triángulo ABC y el paralelogramo DEFG son también equivalentes:
$$ ABC \doteq DEFG $$
Así queda demostrada la primera parte del teorema.
B] Paralelogramo con la misma base y la mitad de la altura del triángulo
Para demostrar la segunda parte del teorema, simétrica a la anterior, aplicaremos un razonamiento diferente.
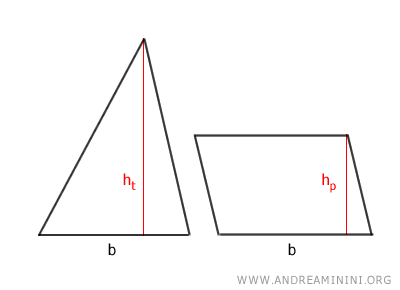
El razonamiento es puramente matemático: el área de un triángulo es la mitad del producto de su base (bt) por su altura (ht):
$$ A_t = \frac{b_t \cdot h_t}{2} $$
El área del paralelogramo es el producto de su base (bp) por su altura (hp):
$$ A_p = b_p \cdot h_p $$
Si la base del triángulo y la del paralelogramo son iguales:
$$ b_p = b_t $$
Denotando la base común como b = bt = bp, tenemos:
$$ A_t = \frac{b \cdot h_t}{2} $$
$$ A_p = b \cdot h_p $$
Las áreas serán iguales si:
$$ A_t = A_p $$
$$ \frac{b \cdot h_t}{2} = b \cdot h_p $$
Dividiendo ambos miembros por b:
$$ \frac{h_t}{2} = h_p $$
Por tanto, el paralelogramo tiene la misma área que el triángulo cuando su altura es la mitad de la altura del triángulo:
$$ h_p = \frac{h_t}{2} $$
Queda así demostrada la segunda parte del teorema.
Nota: Este mismo razonamiento puede aplicarse a la primera parte del teorema (misma altura): $$ A_t = \frac{b_t \cdot h}{2} $$ $$ A_p = b_p \cdot h $$ Siendo h = ht = hp, se tiene: $$ \frac{b_t \cdot h}{2} = b_p \cdot h $$ Simplificando: $$ \frac{b_t}{2} = b_p $$ Es decir, el paralelogramo tiene la misma área que el triángulo cuando su base es la mitad de la base del triángulo.
Y así sucesivamente.