Teorema de equivalencia de los paralelogramos
Dos paralelogramos son equivalentes si tienen bases congruentes y alturas correspondientes iguales.
Este es uno de los criterios de equivalencia más conocidos y utilizados en geometría.
Un ejemplo práctico
Observemos estos dos paralelogramos.
A pesar de tener formas distintas, ambos comparten la misma base (b=5) y la misma altura (h=3).
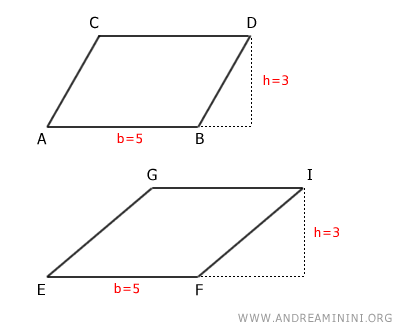
Por consiguiente, sus áreas son iguales.
Para comprobarlo, basta con aplicar la fórmula del área de un paralelogramo:
$$ A = b \cdot h $$
donde "b" representa la base y "h" la altura del paralelogramo.
$$ A = b \cdot h = 5 \cdot 3 = 15 $$
El resultado es idéntico para ambos paralelogramos.
Demostración
Para demostrar este teorema, consideremos dos paralelogramos, ABCD y EFGI.
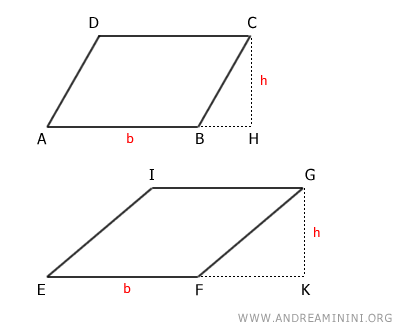
Según la hipótesis inicial, ambos paralelogramos presentan bases congruentes y alturas congruentes:
$$ \overline{AB} \cong \overline{EF} $$
$$ \overline{HC} \cong \overline{KG} $$
Lo que se desea demostrar es que estos dos paralelogramos son equivalentes, es decir, que tienen igual área.
Para ello, alineamos las bases AB y EF mediante un movimiento rígido.
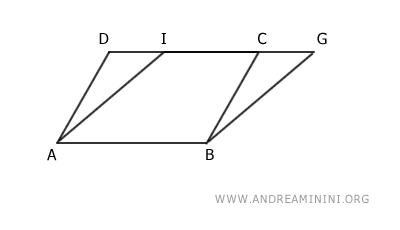
Al superponerlos, aparecen dos triángulos: ADI y BCG.
Los ángulos α y β de estos triángulos son congruentes, ya que sus lados correspondientes son paralelos y coinciden con los lados de los paralelogramos, que por definición son paralelos: AD≅BC y AI≅BG.
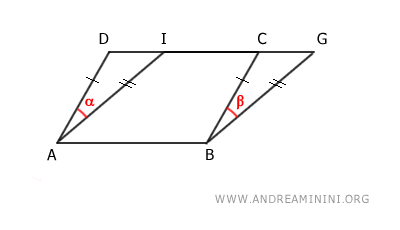
Por lo tanto, según el primer criterio de congruencia de triángulos, los triángulos ADI y BCG son congruentes, pues poseen dos lados congruentes (AD≅BC y AI≅BG) y el ángulo comprendido α≅β.
$$ ADI \cong BCG $$
Ahora bien, el área del paralelogramo ABCD puede considerarse como la diferencia entre el trapecio ABGD y el triángulo BCG:
$$ ABCD \doteq ABGD - BCG $$
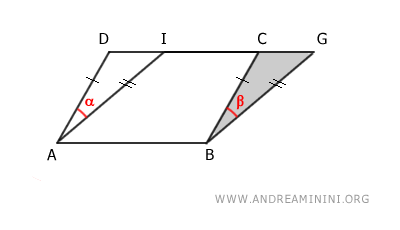
De manera análoga, el área del paralelogramo ABGI se puede expresar como la diferencia entre el mismo trapecio ABGD y el triángulo ADI:
$$ ABGI \doteq ABGD - ADI $$
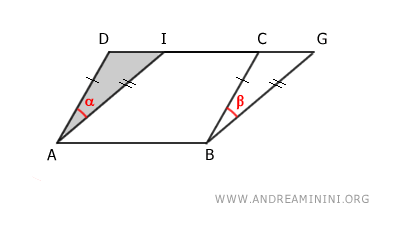
Dado que los triángulos ADI y BCG son congruentes, se deduce que las áreas de los paralelogramos ABCD y ABGI son iguales (superficies equivalentes), pues en ambos casos se obtiene restando al mismo trapecio dos triángulos congruentes:
$$ ABCD \doteq ABGD - BCG \doteq ABGD - ADI \doteq ABGI $$
$$ ABCD \doteq ABGI $$
Además, como por construcción los paralelogramos ABGI y EFGI son congruentes, se concluye que los paralelogramos originales ABCD y EFGI son polígonos equivalentes, es decir, tienen exactamente la misma área:
$$ ABCD \doteq EFGI $$
Observaciones
Algunas observaciones, corolarios y comentarios complementarios:
- Dos rectángulos son equivalentes si tienen bases y alturas congruentes
El rectángulo no es más que un caso particular de paralelogramo con ángulos rectos. Por tanto, el teorema de equivalencia de los paralelogramos se aplica directamente a los rectángulos.
Y así sucesivamente.