Segmento Circular
Un segmento circular es una porción de un círculo delimitada por un arco y la cuerda que une los extremos de dicho arco.
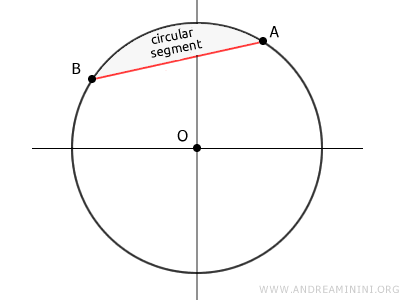
En términos sencillos, es el área comprendida dentro de un círculo entre una cuerda y el arco situado por encima de ella.
A este tipo de región también se le conoce como segmento circular de una sola base.
Una cuerda es, esencialmente, un segmento recto que conecta dos puntos distintos sobre la circunferencia de un círculo. La longitud de la cuerda y del arco que abarca determinan tanto el tamaño como la forma del segmento circular. Por su parte, el arco es la porción de la circunferencia comprendida entre los extremos de la cuerda.
Fórmulas del Segmento Circular
El área Asc de un segmento circular se obtiene restando el área del triángulo formado por la cuerda y los radios del círculo al área del sector circular As.
$$ A_{sc} = \frac{r^2}{2} \cdot \left( \frac{\pi \alpha}{180°} - \sin \alpha \right) $$
donde α es el ángulo central en grados, y r es el radio del círculo.
Nota: El ángulo central está formado por los dos radios que parten del centro del círculo hacia los extremos de la cuerda. La medida de este ángulo determina la longitud del arco y, por ende, el área del segmento circular.
Expresada en radianes, la fórmula para el área es:
$$ A_{sc} = \frac{1}{2} \cdot r^2 \cdot \left( \alpha - \sin \alpha \right) $$
Demostración: El área de un sector circular con un ángulo central α (en grados) se calcula mediante la expresión $$ \frac{\alpha}{360} \cdot \pi r^2 $$. El área de un triángulo cuyos vértices se encuentran en los extremos de la cuerda y en el centro del círculo puede hallarse con la fórmula trigonométrica para el área de un triángulo basada en dos lados y el ángulo comprendido: $$ \frac{1}{2} \cdot a \cdot b \cdot \sin \alpha $$ donde a y b son los lados, y α es el ángulo entre ellos. En el caso del triángulo formado por los extremos de la cuerda y el centro del círculo, ambos lados miden r. Así, el área del triángulo es: $$ \frac{1}{2} \cdot r^2 \cdot \sin \alpha $$ Por tanto, el área del segmento circular se obtiene restando el área del triángulo al área del sector circular: $$ A_{sc} = \frac{\alpha}{360} \cdot \pi r^2 - \frac{1}{2} r^2 \sin(\alpha) $$. Extrayendo el factor común \( \frac{r^2}{2} \), se obtiene la fórmula para el área del segmento circular en grados: $$ A_{sc} = \frac{r^2}{2} \cdot \left( \frac{\pi \alpha}{180°} - \sin \alpha \right) $$. Para convertirla a radianes, basta sustituir los 180° por π radianes y simplificar: $$ A_{sc} = \frac{r^2}{2} \cdot \left( \frac{\pi \alpha}{\pi} - \sin \alpha \right) $$ $$ A_{sc} = \frac{r^2}{2} \cdot \left( \alpha - \sin \alpha \right) $$
Si el segmento circular representa menos de la mitad del círculo, su área se obtiene restando el área del triángulo OAB al área del sector circular correspondiente.
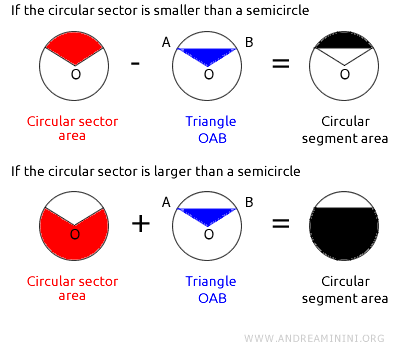
Por el contrario, si el segmento circular abarca más de la mitad del círculo (es decir, supera el semicírculo), su área se determina sumando el área del sector circular y la del triángulo OAB.
La longitud del arco L que abarca la cuerda se calcula mediante:
$$ L = \frac{\alpha}{180} \cdot \pi r $$
Segmento Circular con Dos Bases
Un segmento circular con dos bases es la parte de un círculo comprendida entre dos cuerdas paralelas.
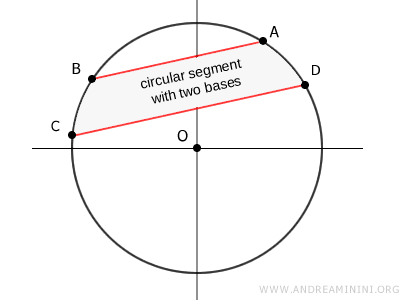
El área de un segmento circular con dos bases se halla restando al área total A del círculo las áreas de los dos segmentos delimitados por las cuerdas AB y CD.
Y así sucesivamente.