Teorema de la Proporcionalidad de las Cuerdas en una Circunferencia
Cuando dos cuerdas se cruzan dentro de una circunferencia, los segmentos en que quedan divididas guardan entre sí una proporción: los segmentos de una cuerda funcionan como términos medios, y los de la otra como términos extremos de la proporción.
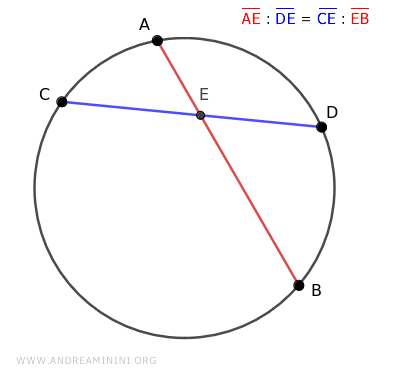
No importa qué cuerda elijamos para representar los extremos y cuál los medios; la proporción siempre se cumple.
Se trata de una propiedad propia de la semejanza en las circunferencias.
Nota. En una proporción, los términos medios son los del centro, mientras que los extremos se sitúan a ambos lados.
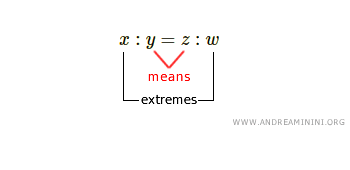
Un Ejemplo Práctico
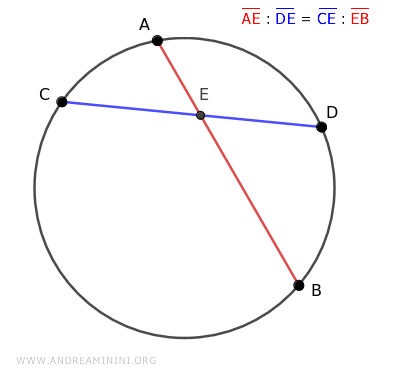
Consideremos, por ejemplo, una circunferencia en la que dos cuerdas, AB y CD, se cruzan en el punto E, en el interior de la circunferencia.
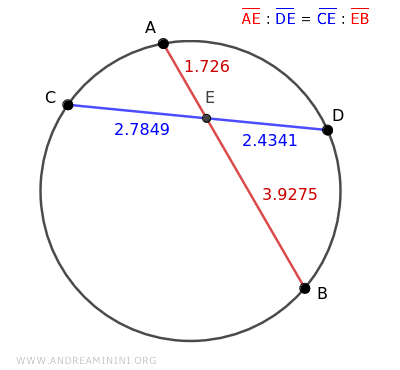
Según el teorema de las cuerdas, los segmentos de una cuerda constituyen los términos medios en la proporción, mientras que los segmentos de la otra son los términos extremos.
$$ \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
En este caso, los términos medios de la proporción son los segmentos de la cuerda azul CD, y los extremos corresponden a la cuerda roja AB.
Sustituyamos las longitudes de los segmentos.
$$ 1.726 : 2.4341 = 2.7849 : 3.9275 $$
Al calcular ambos cocientes, obtenemos el mismo valor.
$$ 0.709 = 0.709 $$
Por lo tanto, la proporción se cumple perfectamente.
Nota. Evidentemente, si invertimos la proporción, el resultado es el mismo. Por ejemplo, si tomamos los segmentos de la cuerda roja AB como términos medios y los de la cuerda CD como extremos, la igualdad sigue cumpliéndose. $$ \overline{DE} : \overline{AE} = \overline{EB} : \overline{CE} $$ $$ 2.4341 : 1.726 = 3.9275 : 2.7849 $$ $$ 1.41 : 1.41 $$
Demostración
Partamos de una circunferencia.
Dibujamos dos cuerdas secantes, AB y CD, que se cruzan en su interior en el punto E.
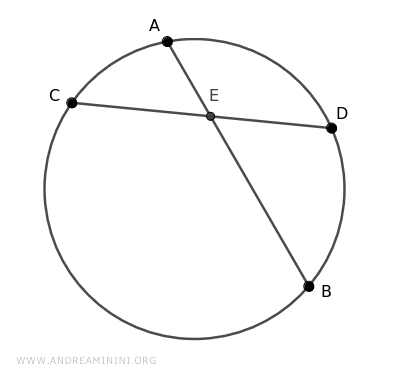
Unimos los extremos de las cuerdas mediante los segmentos AC y BD.
Así se forman dos triángulos: ACE y BDE.
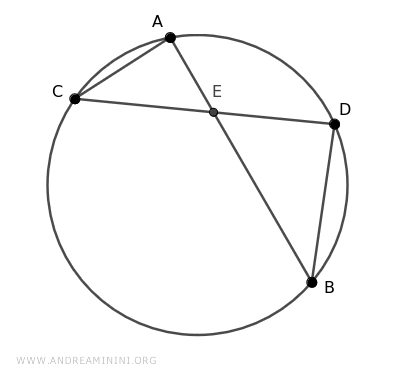
Estos dos triángulos comparten un ángulo congruente α≅α' en el vértice E, puesto que α y α' son ángulos opuestos por el vértice.
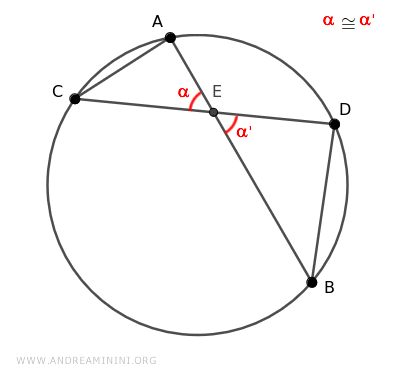
Además, comparten otro par de ángulos congruentes β≅β', ya que los ángulos β y β' son ángulos inscritos que abarcan el mismo arco AD de la circunferencia.
Por tanto, según el teorema de los ángulos inscritos, estos ángulos son iguales.
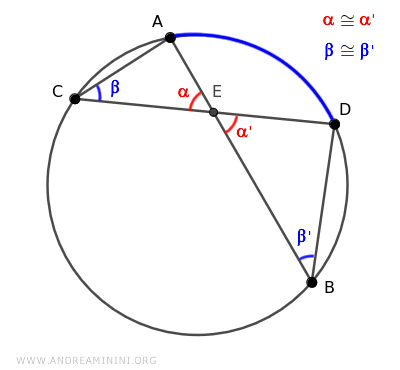
En consecuencia, de acuerdo con el primer criterio de semejanza de triángulos, los triángulos ACE y BDE son semejantes, pues comparten dos ángulos congruentes α≅α' y β≅β'.
Al ser semejantes, los lados de los triángulos ACE y BDE guardan la misma proporción.
$$ \overline{AC} : \overline{BD} = \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
Nota. Para identificar los lados correspondientes basta fijarse en los lados opuestos a los ángulos congruentes en cada triángulo. Por ejemplo, sabiendo que α≅α', el lado opuesto al ángulo α en el triángulo ACE es AC, mientras que el opuesto a α' en el triángulo BDE es BD. Por tanto, AC y BD son lados correspondientes.
La proporción que acabamos de demostrar confirma el teorema inicial.
$$ \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
Los segmentos de una cuerda, DE y CE, son los términos medios, mientras que los segmentos de la otra, AE y EB, son los términos extremos de la proporción.
Y así sucesivamente.