Teorema del Área de Polígonos Semejantes
Para dos polígonos semejantes, la razón entre sus áreas es igual al cuadrado de su razón de semejanza o factor de escala: $ \frac{A}{A'} = k^2 $.
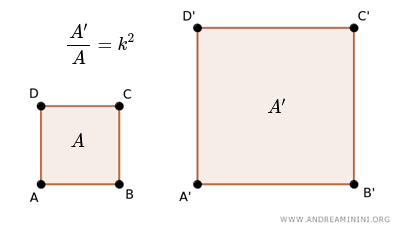
En otras palabras, la relación entre las áreas de dos polígonos semejantes equivale al cuadrado de la proporción entre las longitudes de sus lados correspondientes.
$$ \frac{A'}{A} = k^2 = \left( \frac{l}{l'} \right)^2 $$
Donde \( k \) representa el factor de escala, y \( l \), \( l' \) son las longitudes de lados homólogos en ambos polígonos.
Esto implica que, si un polígono es \( k \) veces mayor que otro semejante, su área será \( k^2 \) veces la del polígono más pequeño.
$$ A' = A \cdot k^2 $$
Así, las áreas - al ser magnitudes bidimensionales - crecen proporcionalmente al cuadrado del factor de semejanza, lo que explica la relación \( k^2 \).
Por ejemplo, si tenemos dos cuadrados donde el lado de uno mide el doble que el del otro, el área del cuadrado mayor será cuatro veces la del menor.
Ejemplo Práctico
Consideremos dos cuadrados semejantes.
Uno tiene lados de 2 unidades, mientras que el otro tiene lados de 4 unidades.
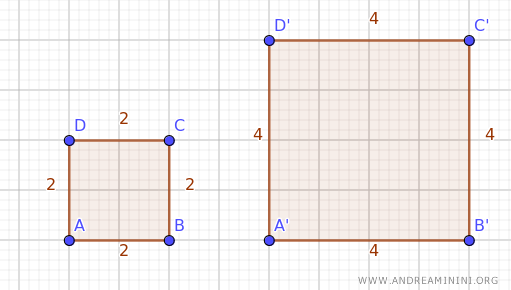
La razón de semejanza entre ambos cuadrados es \( k = 2 \), lo que indica que los lados del segundo cuadrado son el doble de largos que los del primero.
$$ k = \frac{\overline{A'B'}}{\overline{AB}} = \frac{4}{2} = 2 $$
Calculemos ahora las áreas de los dos cuadrados.
$$ A = \overline{AB} \cdot \overline{BC} = 2 \times 2 = 4 $$
$$ A' = \overline{A'B'} \cdot \overline{B'C'} = 4 \times 4 = 16 $$
Por lo tanto, el área del cuadrado mayor resulta ser exactamente cuatro veces la del cuadrado menor.
Demostración
Consideremos dos polígonos semejantes, como el caso de dos cuadrados.
Al ser semejantes, todos sus lados mantienen la misma proporción, es decir, comparten el mismo factor de escala \( k \).
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{B'C'}}{\overline{BC}} = k $$
Llamemos al segmento AB la base \( b \) y al segmento BC la altura \( h \) del polígono.
$$ \frac{\overline{b'}}{\overline{b}} = \frac{\overline{h'}}{\overline{h}} = k $$
De lo cual se deduce:
$$ b' = k \cdot b $$
$$ h' = k \cdot h $$
Calculemos ahora el área del segundo cuadrado:
$$ A' = b' \cdot h' $$
Sustituyendo las expresiones de \( b' \) y \( h' \):
$$ A' = (b \cdot k) \cdot (h \cdot k) $$
$$ A' = b \cdot h \cdot k^2 $$
Como el producto \( b \cdot h \) es precisamente el área del primer cuadrado, es decir, \( A \), obtenemos:
$$ A' = A \cdot k^2 $$
Así queda demostrado que la razón entre las áreas de dos polígonos semejantes es el cuadrado de su razón de semejanza.
$$ \frac{A'}{A} = k^2 $$
Y este principio se aplica a cualquier tipo de polígono, no solo a los cuadrados. El razonamiento es idéntico, ya se trate de triángulos u otras figuras geométricas.
Y con esto queda probado.