Cuerdas de una circunferencia
Una cuerda es un segmento recto que une dos puntos distintos situados sobre la circunferencia de un círculo.
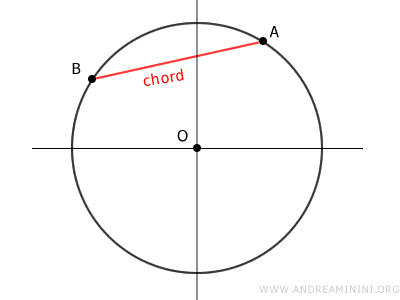
El diámetro constituye un caso particular de cuerda, ya que es la más larga que puede trazarse en el interior de una circunferencia.
A diferencia del diámetro, ninguna otra cuerda atraviesa el centro de la circunferencia.
En un sentido más amplio, se denomina cuerda a cualquier segmento cuyos extremos se ubican en dos puntos distintos de una curva, como ocurre en una circunferencia, una elipse o una hipérbola, o bien en lados opuestos de un polígono. Es importante tener presente que las propiedades de las cuerdas pueden variar según la curva a la que pertenezcan.
Las cuerdas dividen la circunferencia en dos arcos.
Por eso se dice que una cuerda subtiende dos arcos o, dicho de otra forma, cada arco está subtenido por la cuerda.
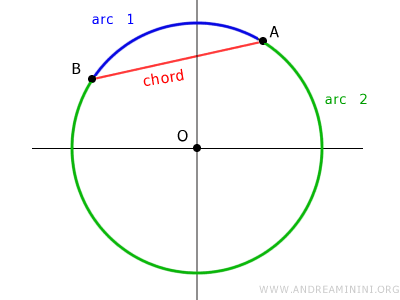
Así, para especificar a qué arco de una cuerda se hace referencia, es necesario añadir un tercer punto sobre el arco o adoptar alguna convención, como por ejemplo recorrerlo en sentido horario entre sus extremos.
La recta que contiene a una cuerda se conoce como secante.
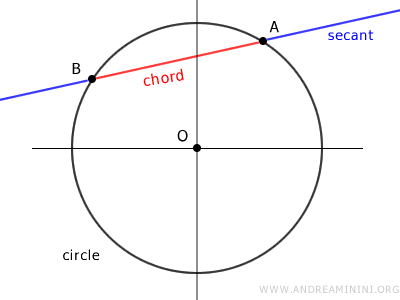
Una cuerda, junto con el arco correspondiente, delimita una superficie finita conocida como segmento circular, o simplemente segmento curvilíneo si forma parte de cualquier otra curva.
Aspectos interesantes
Curiosidades y propiedades sobre las cuerdas de una circunferencia
- La mediatriz de cualquier cuerda pasa por el centro de la circunferencia
Si se toma una cuerda cuyos extremos son A y B sobre la circunferencia, su mediatriz - la recta perpendicular que pasa por el punto medio - atraviesa siempre el centro de la circunferencia.
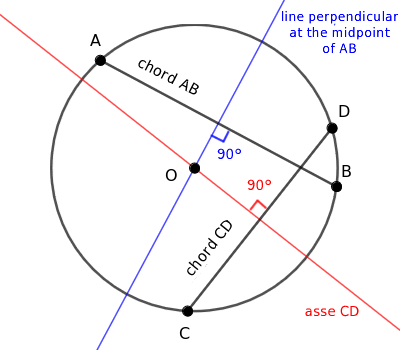
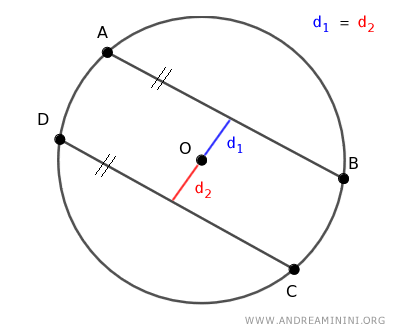
- Dos cuerdas son congruentes si y solo si están a la misma distancia del centro de la circunferencia
Para que dos cuerdas AB y CD sean congruentes, deben situarse a la misma distancia del centro O de la circunferencia, es decir, d1 = d2.
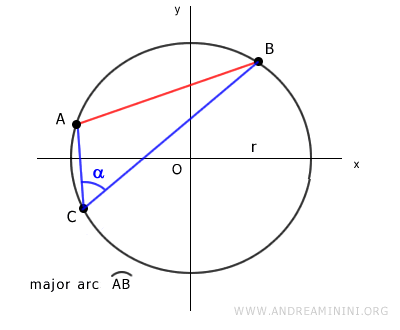
- Teorema de la cuerda
La longitud de la cuerda AB de una circunferencia de radio r es igual al doble del radio multiplicado por el seno de uno de los ángulos α que subtiende en la circunferencia. $$ AB = 2r \sin \alpha $$
Y la lista podría continuar.