Teorema de las cuerdas equidistantes del centro
En una circunferencia, dos cuerdas congruentes se encuentran a la misma distancia del centro, y de manera recíproca, dos cuerdas situadas a igual distancia del centro son congruentes.
Esto implica que también se cumple la recíproca: dos cuerdas equidistantes del centro necesariamente son congruentes.
Demostración
La demostración se puede dividir en dos partes.
A] Dos cuerdas equidistantes del centro son congruentes
Queremos demostrar que dos cuerdas que se encuentran a la misma distancia del centro O de la circunferencia son congruentes.
Consideremos una circunferencia y dos cuerdas AB y CD que están a igual distancia del centro O.
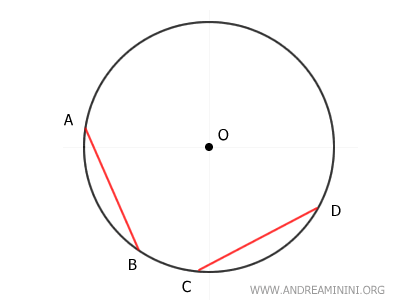
Desde O se trazan segmentos perpendiculares hasta cada cuerda para representar sus distancias al centro.
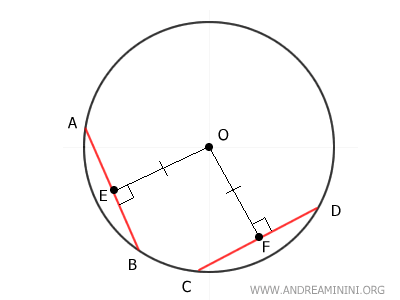
Nota. La distancia se mide mediante un segmento perpendicular trazado desde el centro O hasta la cuerda AB (o CD).
Por hipótesis, esas distancias son iguales:
$$ \overline{OE} \cong \overline{OF} $$
Se trazan ahora los segmentos OB y OD. Como ambos son radios de la circunferencia, son congruentes:
$$ \overline{OB} \cong \overline{OD} $$
Con esta construcción se forman dos triángulos rectángulos: OBE y ODF.
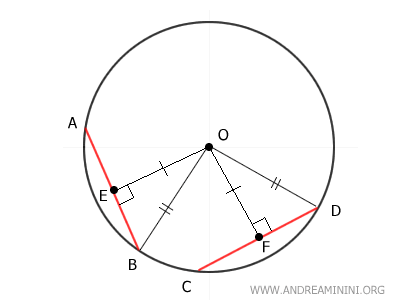
Los triángulos OBE y ODF son congruentes, ya que tienen dos pares de lados iguales: OB ≅ OD y OE ≅ OF.
$$ OBE \cong ODF $$
De esta congruencia se deduce que sus partes correspondientes son iguales. En particular, los segmentos BE ≅ DF son congruentes.
$$ \overline{BE} \cong \overline{DF} $$
Después se trazan los segmentos OA y OC, formando los triángulos OAB y OCD.
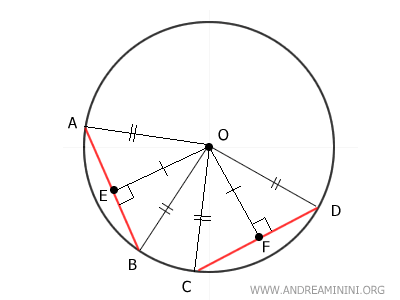
Dado que OA y OC son radios de la circunferencia, son congruentes entre sí OA ≅ OC y también con los otros radios OB y OD:
$$ \overline{OA} \cong \overline{OC} \cong \overline{OB} \cong \overline{OD} $$
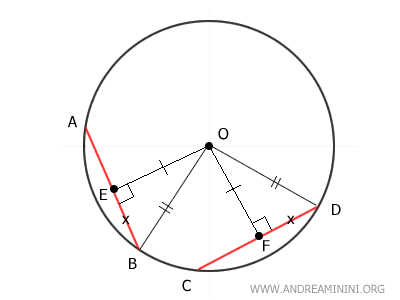
Por lo tanto, los triángulos AOB y COD son triángulos isósceles, ya que ambos tienen dos lados congruentes: OA ≅ OB y OC ≅ OD.
En un triángulo isósceles, la altura coincide con la mediana, por lo que los segmentos AE ≅ BE y CF ≅ DF son congruentes.
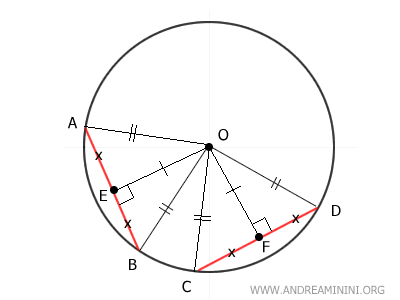
Como ya sabemos que BE ≅ DF, al duplicar estos segmentos se concluye que 2BE ≅ 2DF.
Y dado que 2BE representa la longitud de la cuerda AB (es decir, 2BE ≅ AB) y 2DF representa la cuerda CD (es decir, 2DF ≅ CD), se deduce que las cuerdas AB y CD son congruentes:
$$ \overline{AB} \cong \overline{CD} $$
Así queda demostrado que dos cuerdas equidistantes del centro O de una circunferencia son congruentes.
B] Dos cuerdas congruentes están equidistantes del centro de la circunferencia
Consideremos ahora dos cuerdas AB y CD, que por hipótesis son congruentes, es decir, AB ≅ CD.
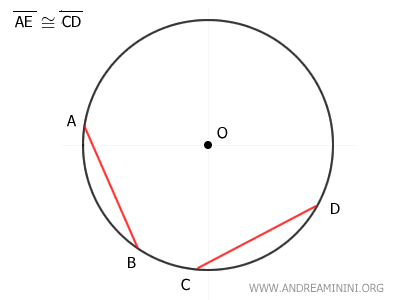
Se trazan los segmentos OA, OB, OC y OD. Como todos son radios, son congruentes: OA ≅ OB ≅ OC ≅ OD.
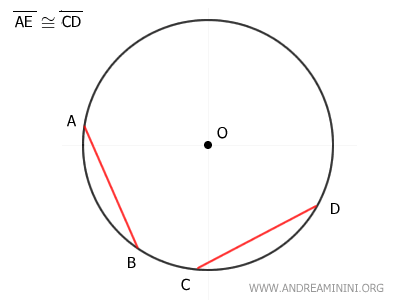
Los triángulos OAB y OCD son congruentes por el criterio Lado-Lado-Lado (LLL):
$$ OAB \cong OCD $$
Además, ambos son triángulos isósceles, pues cada uno tiene dos lados congruentes: OA ≅ OB y OC ≅ OD.
En un triángulo isósceles, la mediana coincide con la altura, es decir, con el segmento que va desde el vértice hasta el punto medio del lado opuesto.
En este caso, los segmentos OE y OF son las alturas de los triángulos y son congruentes: OE ≅ OF, puesto que los triángulos son congruentes.
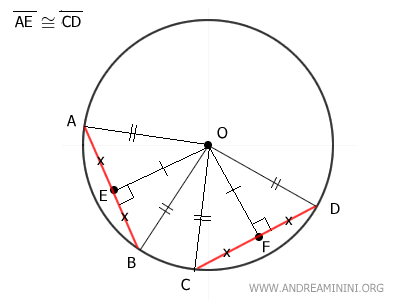
Las alturas OE ≅ OF son perpendiculares a las cuerdas y parten del centro O de la circunferencia. Por lo tanto, estos segmentos representan la distancia de las cuerdas al centro.
Esto demuestra que dos cuerdas congruentes están equidistantes del centro de la circunferencia.
Y así continúa el razonamiento.