El Diámetro es Mayor que Cualquier Cuerda que No Pase por el Centro
En una circunferencia, el diámetro siempre es mayor que cualquier cuerda que no pase por el centro.
Demostración
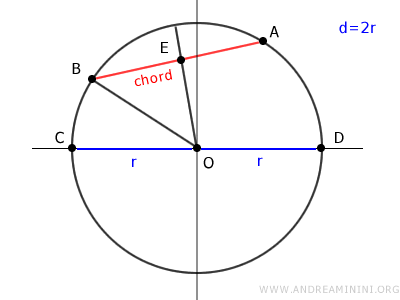
Sea una circunferencia de centro O, una cuerda AB que no pasa por el centro, y un diámetro CD.
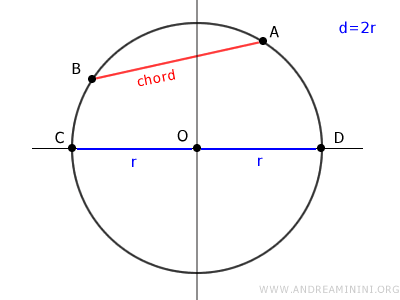
Los puntos O, A y B determinan el triángulo rectángulo OAB.
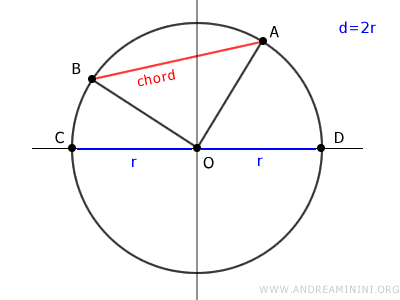
Según el teorema de la desigualdad triangular, en todo triángulo, cualquier lado es menor que la suma de los otros dos.
Por tanto, la longitud de la cuerda AB es menor que la suma de los segmentos OA y OB.
$$ \overline{AB} < \overline{OA} + \overline{OB} $$
Como OA y OB son radios de la circunferencia, se cumple que OA = r y OB = r.
Podemos entonces expresar la desigualdad sustituyendo OA y OB por el radio (r) de la circunferencia.
$$ \overline{AB} < r + r $$
$$ \overline{AB} < 2r $$
Como sabemos que el segmento CD es el diámetro (d) de la circunferencia y equivale al doble del radio, es decir, CD = 2r, podemos reemplazar 2r por el diámetro (d).
$$ \overline{AB} < 2r $$
Así, dado que el diámetro d = 2r es el doble del radio, tenemos que
$$ \overline{AB} < d $$
Esto prueba que cualquier cuerda que no pase por el centro de la circunferencia es más corta que el diámetro (d).
Demostración Alternativa
Consideremos nuevamente una circunferencia de centro O, una cuerda AB que no pasa por el centro, y un diámetro CD.
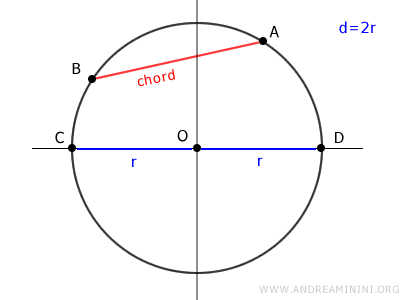
Se traza el segmento OB.
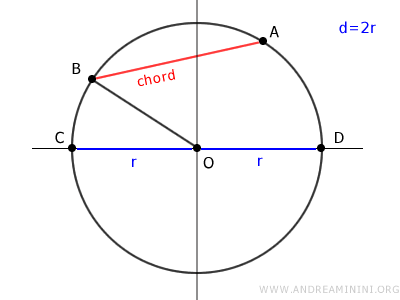
Se dibuja un radio que pase por el punto medio E de la cuerda AB.
Dado que la mediatriz de una cuerda siempre pasa por el centro de la circunferencia, se deduce que un radio que biseca una cuerda es perpendicular a dicha cuerda.
En consecuencia, el triángulo OBE es rectángulo.
Según el teorema de Pitágoras, en un triángulo rectángulo, la hipotenusa siempre es mayor que cualquiera de sus catetos. Por lo tanto, OB > BE.
$$ \overline{OB} > \overline{BE} $$
Aplicando la propiedad invariante, multiplicamos ambos términos de la desigualdad por dos.
$$ 2 \cdot \overline{OB} > 2 \cdot \overline{BE} $$
Como OB = r, y el doble del radio, 2r = CD, corresponde al diámetro (d), se tiene que
$$ \overline{CD} > 2 \cdot \overline{BE} $$
Siendo E el punto medio de la cuerda AB, se cumple que 2·BE es igual a la longitud de la cuerda AB.
$$ \overline{CD} > \overline{AB} $$
Esto demuestra que el diámetro (CD) siempre es mayor que cualquier cuerda (AB) que no pase por el centro de la circunferencia.
Y así sucesivamente.