Teorema de las cuerdas no congruentes
En una circunferencia, dos cuerdas que no son congruentes no se encuentran a la misma distancia del centro. La cuerda más corta se sitúa más lejos del centro y viceversa.
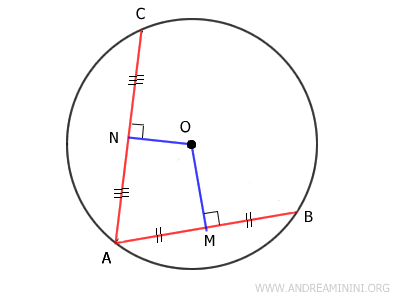
Demostración
Consideremos dos cuerdas no congruentes, AB y AC, trazadas en una circunferencia, siendo AC mayor que AB, es decir, AC > AB.
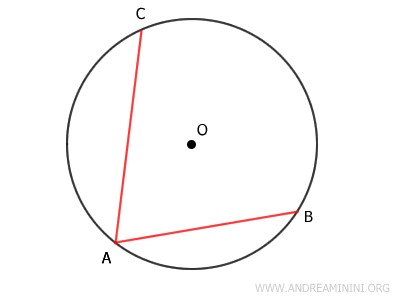
Se trazan los radios OA, OB y OC, los cuales son congruentes entre sí: OA ≅ OB ≅ OC, ya que una circunferencia se define como el lugar geométrico de todos los puntos equidistantes de su centro O.
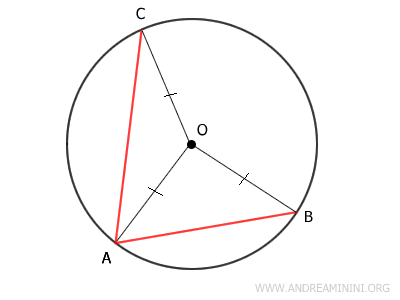
Esta construcción da lugar a dos triángulos: AOB y AOC.
Ambos, AOB y AOC, son triángulos isósceles, pues poseen dos lados congruentes.
En los triángulos isósceles, la mediana coincide con la altura. Por lo tanto, los puntos M y N son los puntos medios de las cuerdas AB y AC, respectivamente.
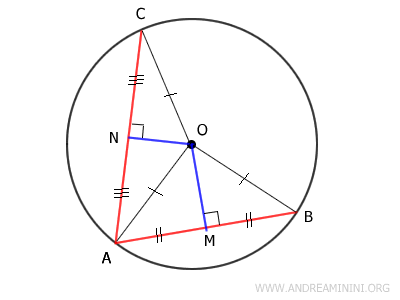
A continuación, se traza el segmento MN, que une los puntos medios M y N.
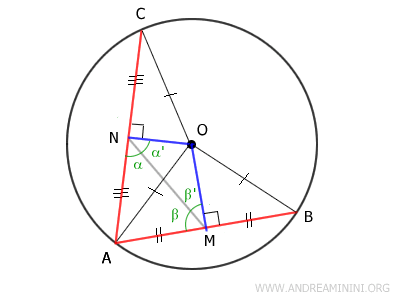
Dicho segmento MN determina dos pares de ángulos complementarios:
$$ \alpha + \alpha' = 90^\circ $$
$$ \beta + \beta' = 90^\circ $$
En el triángulo AMN, el lado AN es mayor que AM porque, según nuestra hipótesis, AC > AB. Dado que AN es la mitad de AC y AM la mitad de AB, se sigue que AN > AM:
$$ \overline{AN} > \overline{AM} $$
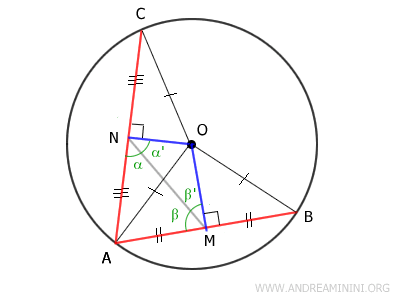
En el triángulo AMN, si AN es mayor que AM, los ángulos opuestos a estos lados guardan la misma relación.
El ángulo β se opone al lado AN, mientras que el ángulo α se opone al lado AM:
$$ \beta > \alpha $$
Como sabemos que α + α′ = 90° y β + β′ = 90°, se deduce que la relación entre sus ángulos complementarios se invierte:
$$ \beta' < \alpha' $$
Dado que β' < α', podemos aplicar el mismo teorema y concluir que los lados opuestos a estos ángulos también cumplen la misma desigualdad. Por lo tanto, ON < OM.
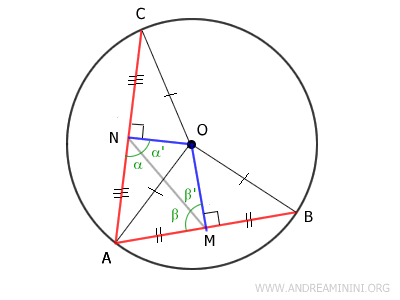
En consecuencia, el segmento OM resulta mayor que el segmento ON:
$$ \overline{OM} > \overline{ON} $$
Esto demuestra que la cuerda más corta, AB, se encuentra más alejada del centro (OM > ON) que la cuerda más larga, AC.
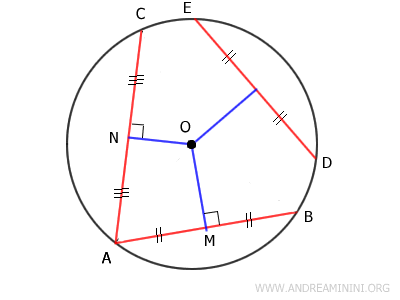
Y dado que cualquier cuerda DE congruente con AB está a la misma distancia del centro, se concluye que toda cuerda más corta que AC se sitúa más lejos del centro.
Y así continúa el razonamiento.