Teorema del diámetro que pasa por el punto medio de una cuerda

En una circunferencia, si un diámetro pasa por el punto medio de una cuerda que no atraviesa el centro, entonces dicho diámetro es perpendicular a esa cuerda.

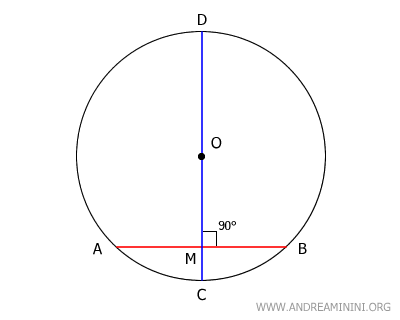
Demostración

Consideremos una cuerda AB que no pasa por el centro O de la circunferencia, y un diámetro CD que atraviesa el punto medio M de la cuerda.

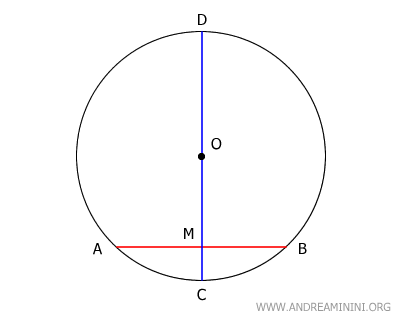
Unimos los extremos A y B de la cuerda con el centro O mediante los segmentos OA y OB, formando así el triángulo ABO.

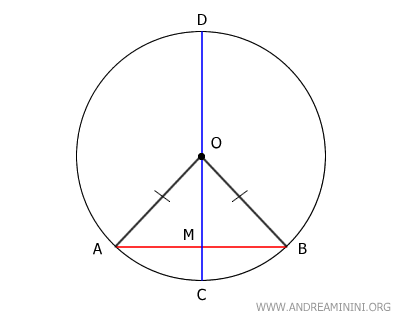
Dado que OA y OB son radios de la circunferencia, son congruentes:

$$ \overline{AO} \cong \overline{BO} $$

Al tener dos lados iguales, el triángulo ABO es un triángulo isósceles.

En un triángulo isósceles, la mediana trazada desde el vértice hasta la base coincide también con la altura, la bisectriz y la mediatriz perpendicular.

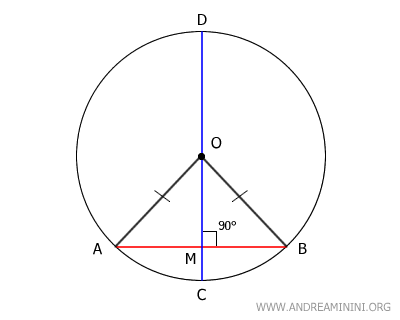
En este caso, el segmento OM ejerce simultáneamente la función de mediana y de altura del triángulo. Por tanto, OM es perpendicular a AB y forma un ángulo recto de 90°.

Como OM se encuentra sobre el diámetro CD, se concluye que el diámetro CD es perpendicular a la cuerda AB.

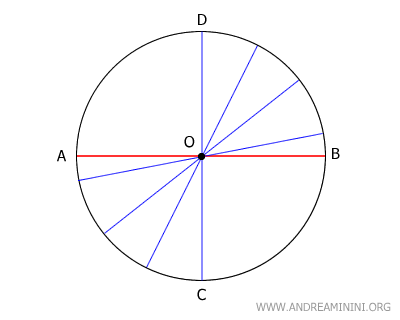
Nota. Conviene destacar que este teorema solo es válido cuando la cuerda AB no pasa por el centro O de la circunferencia. Si la cuerda pasara por O, su punto medio coincidiría siempre con el centro de la circunferencia. En ese caso, cualquier diámetro pasaría por el centro, formando ángulos de distintas medidas. En esencia, el punto O se convierte en el origen de un haz de rectas que se extienden en todas las direcciones.

Y así continúa el razonamiento.