Teorema de la mediatriz de una cuerda
En una circunferencia, la mediatriz de cualquier cuerda pasa siempre por el centro de la circunferencia.
Demostración
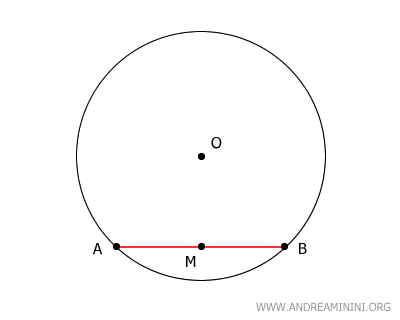
Consideremos una cuerda AB y llamemos M a su punto medio.
Unimos los extremos A y B de la cuerda con el centro O mediante los segmentos OA y OB. De este modo se forma el triángulo ABO.
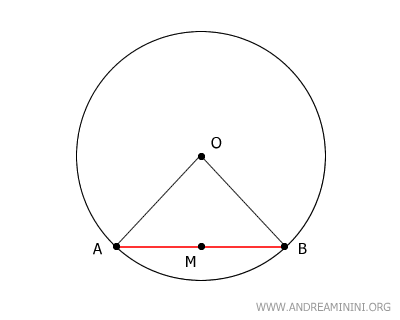
Los segmentos OA y OB son congruentes, ya que ambos son radios de la circunferencia.
$$ \overline{OA} \cong \overline{OB} $$
Al ser OA y OB iguales, el triángulo ABO es un triángulo isósceles.
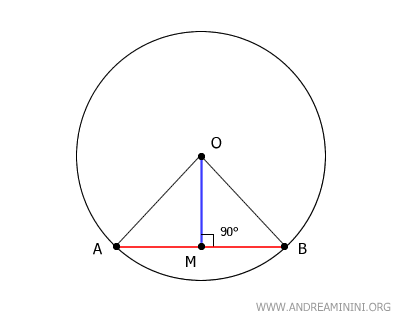
En un triángulo isósceles, la mediana trazada desde el vértice O hasta el punto medio M de la base AB coincide también con la altura, la bisectriz y la mediatriz perpendicular.
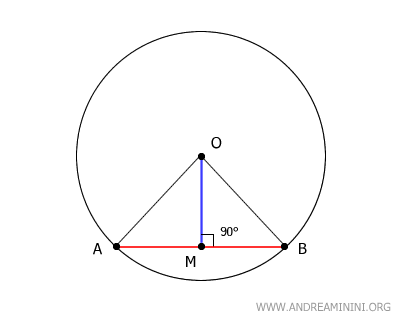
En este caso, el segmento OM actúa como mediana y, al mismo tiempo, como altura del triángulo. Por lo tanto, OM es perpendicular a AB y forma un ángulo recto de 90°.
Además, el segmento OM es la mediatriz del segmento AB, ya que es perpendicular a AB y pasa por M, el punto medio de dicha cuerda.
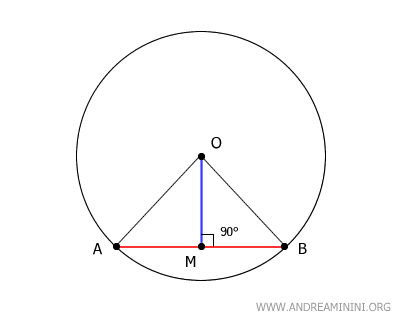
Por construcción, uno de los extremos del segmento OM coincide exactamente con el centro O de la circunferencia.
Esto demuestra que la mediatriz de cualquier cuerda siempre pasa por el centro de la circunferencia.
Y así continúa el razonamiento.