Teorema del diámetro perpendicular a una cuerda
En una circunferencia, si un diámetro es perpendicular a una cuerda, entonces la cuerda, el ángulo central y el arco correspondiente quedan divididos exactamente en dos partes iguales.
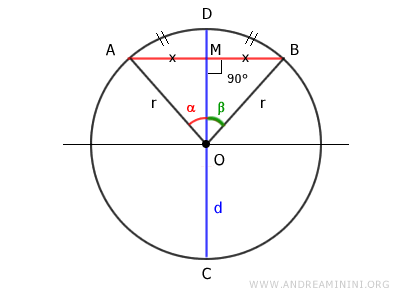
Demostración
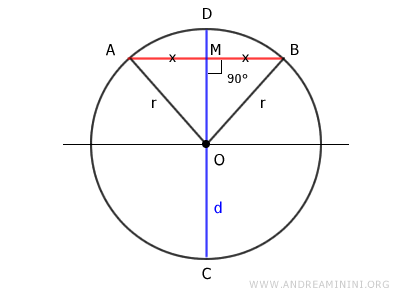
Consideremos una circunferencia con centro en O, una cuerda AB y un diámetro CD.
Por hipótesis inicial, el diámetro es perpendicular a la cuerda.
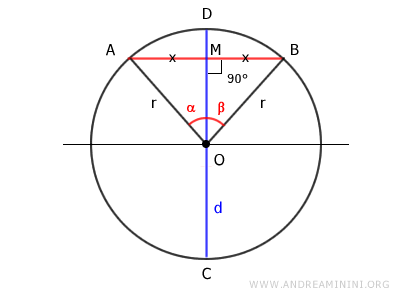
Se trazan los segmentos OA y OB.
De esta forma se obtiene el triángulo OAB.
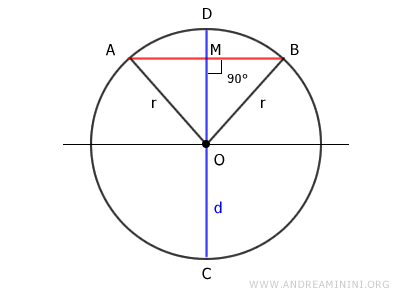
El segmento OM actúa como altura del triángulo, ya que coincide con el diámetro CD y, según nuestra hipótesis, es perpendicular a la cuerda.
Los segmentos OA y OB son radios de la circunferencia, por lo tanto OA = r y OB = r. Esto significa que son congruentes, es decir, OA ≅ OB.
Al ser OA y OB lados congruentes, el triángulo OAB es un triángulo isósceles.
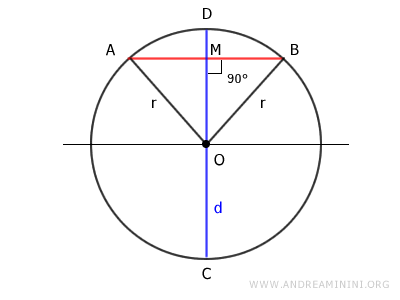
En un triángulo isósceles, la mediana coincide con la altura OM.
Así, el punto M es el punto medio del segmento AB, dividiéndolo en dos partes iguales, es decir, AM = MB.
Esto demuestra que el diámetro biseca la cuerda AB.
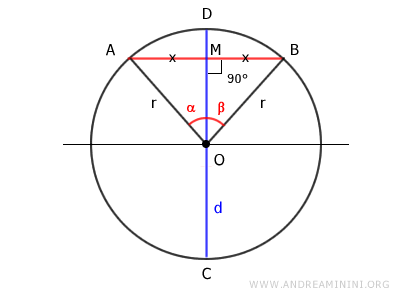
Además, en un triángulo isósceles, la bisectriz también coincide con la altura OM.
Por lo tanto, el ángulo central se divide en dos ángulos iguales, es decir, α ≡ β.
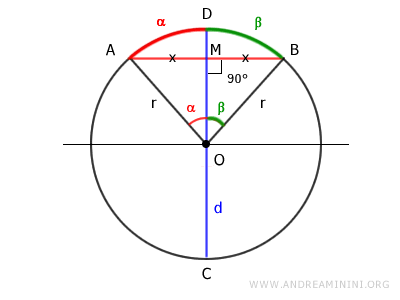
Y como en una circunferencia, dos ángulos centrales iguales α ≅ β abarcan arcos congruentes AD ≅ BD, el arco también queda dividido en dos partes iguales.
Y así continúa el razonamiento.