Circunferencias interiores y concéntricas

Decimos que una circunferencia está contenida dentro de otra, llamada circunferencia exterior, si la distancia entre sus centros \( OO' \) es menor que la diferencia de sus radios: $$ \overline{OO'} < | r - r' | $$

En esta expresión, \( OO' \) indica la distancia entre los centros de ambas circunferencias, mientras que \( r \) y \( r' \) representan los radios de la circunferencia exterior y de la interior, respectivamente.

 

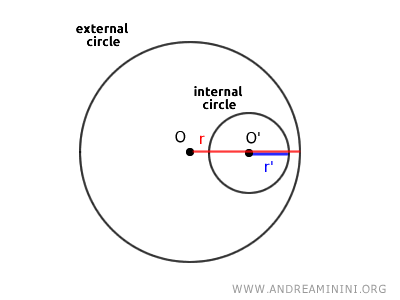
En este contexto, se asume que todos los puntos de una circunferencia se encuentran completamente dentro de la otra.

Para que esto ocurra, deben cumplirse dos condiciones:

• El centro de la circunferencia interior \( O' \) debe estar situado en el interior de la circunferencia exterior.
• La suma del radio de la circunferencia interior \( r' \) y la distancia entre los centros \( OO' \) debe ser menor que el radio de la circunferencia exterior: $$ \overline{OO'} + r' < r $$

Estas condiciones garantizan que todos los puntos de la circunferencia interior queden completamente contenidos dentro de la exterior.

 

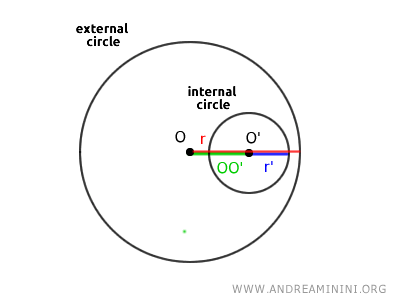
Nota: En el caso particular en que ambas circunferencias comparten el mismo centro \( O = O' \) pero tienen radios distintos \( r \ne r' \), se las denomina circunferencias concéntricas. En este caso, la distancia entre sus centros es nula \( OO' = 0 \).

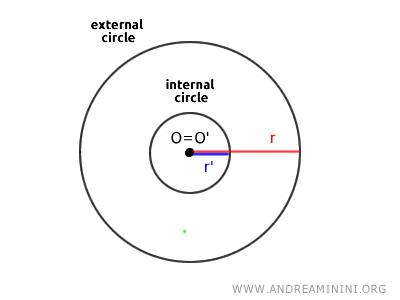
Se denominan circunferencias coincidentes si comparten el mismo centro \( O = O' \) y tienen el mismo radio \( r = r' \).

Un ejemplo práctico

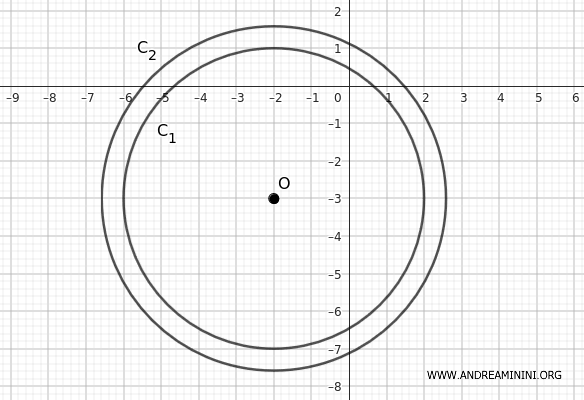
Analicemos el siguiente caso con dos circunferencias:

1. La primera circunferencia \( C_1 \) tiene su centro en \( O_1 = (0, 0) \) y un radio de \( r_1 = 5 \) cm.
2. La segunda circunferencia \( C_2 \) tiene su centro en \( O_2 = (1, 1) \) y un radio de \( r_2 = 2 \) cm.

Calculamos la distancia entre los centros \( O_1 \) y \( O_2 \) aplicando la fórmula de distancia euclídea:

$$ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$

En este caso, \( O_1 = (0, 0) \) y \( O_2 = (1, 1) \), por lo que \( x_1 = 0 \), \( y_1 = 0 \), \( x_2 = 1 \) y \( y_2 = 1 \).

$$ d = \sqrt{(1 - 0)^2 + (1 - 0)^2} $$

$$ d = \sqrt{1 + 1} $$

$$ d = \sqrt{2} \approx 1.41 \text{ cm} $$

A continuación, verificamos si una circunferencia está efectivamente contenida dentro de la otra.

Para que esto ocurra, la distancia entre los centros debe ser menor que la diferencia absoluta de sus radios:

$$ d < | r_1 - r_2 | $$

La distancia entre los centros es aproximadamente \( d = 1.41 \) cm, mientras que los radios son \( r_1 = 5 \) cm y \( r_2 = 2 \) cm.

$$ 1.41 < 5 - 2 $$

$$ 1.41 < 3 $$

Por tanto, la circunferencia de radio menor \( C_2 \) está completamente contenida dentro de la circunferencia de mayor radio \( C_1 \).

Circunferencias interiores en geometría analítica

Para determinar si una circunferencia está contenida dentro de otra a partir de sus ecuaciones, es imprescindible identificar y comparar sus radios y las posiciones de sus centros.

Supongamos que tenemos dos circunferencias con las siguientes ecuaciones:

$$ C_1: x^2 + y^2 + a_1x + b_1y + c_1 = 0 $$

$$ C_2: x^2 + y^2 + a_2x + b_2y + c_2 = 0 $$

El primer paso consiste en hallar los centros y radios de ambas circunferencias.

Nota: Para obtenerlos, podemos usar directamente las fórmulas para el centro $$ \left(-\frac{a}{2}, -\frac{b}{2}\right) $$ y para el radio $$ r = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2 - c} $$. No obstante, prefiero exponer todo el proceso, ya que permite resolver el problema incluso si no se recuerdan dichas fórmulas de memoria.

Para determinar los centros, transformamos las ecuaciones a la forma canónica:

$$ (x-h)^2 + (y-k)^2 = r^2 $$

donde \((h, k)\) es el centro y \(r\) el radio.

1] Primera circunferencia en forma canónica

Consideremos la primera circunferencia \( x^2 + y^2 + a_1x + b_1y + c_1 = 0 \):

\[ x^2 + a_1x + y^2 + b_1y = -c_1 \]

Completamos el cuadrado para los términos en \( x \) y en \( y \):

\[ x^2 + a_1x + \left(\frac{a_1}{2}\right)^2 + y^2 + b_1y + \left(\frac{b_1}{2}\right)^2 = -c_1 + \left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 \]

Así, obtenemos la ecuación en forma canónica:

\[ \left(x + \frac{a_1}{2}\right)^2 + \left(y + \frac{b_1}{2}\right)^2 = \left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 - c_1 \]

De donde se deduce fácilmente el centro y el radio:

• El centro de la primera circunferencia es $$ \left(-\frac{a_1}{2}, -\frac{b_1}{2}\right) $$
• El radio es $$ r_1 = \sqrt{\left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 - c_1} $$

2] Segunda circunferencia en forma canónica

Procedemos del mismo modo para la segunda circunferencia:

$$ x^2 + y^2 + a_2x + b_2y + c_2 = 0 $$

$$ x^2 + y^2 + a_2x + b_2y = -c_2 $$

Completamos el cuadrado en \( x \) y en \( y \):

\[ x^2 + a_2x + \left(\frac{a_2}{2}\right)^2 + y^2 + b_2y + \left(\frac{b_2}{2}\right)^2 = -c_2 + \left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 \]

Obtenemos la ecuación en forma canónica:

\[ \left(x + \frac{a_2}{2}\right)^2 + \left(y + \frac{b_2}{2}\right)^2 = \left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 - c_2 \]

De esta forma identificamos de inmediato su centro y radio:

• El centro de la segunda circunferencia es $$ \left(-\frac{a_2}{2}, -\frac{b_2}{2}\right) $$
• Su radio es $$ r_2 = \sqrt{\left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 - c_2} $$

3] Comparación de la distancia entre centros y la diferencia de radios

Una vez obtenidos los centros y radios, podemos determinar si una circunferencia está contenida dentro de la otra.

Calculamos la distancia entre sus centros:

\[ d = \sqrt{\left(-\frac{a_1}{2} + \frac{a_2}{2}\right)^2 + \left(-\frac{b_1}{2} + \frac{b_2}{2}\right)^2} \]

Y comparamos esta distancia con la suma de los radios:

• Si \( d + r_1 \leq r_2 \), entonces la primera circunferencia está contenida en la segunda.
• Si \( d + r_2 \leq r_1 \), entonces la segunda está contenida en la primera.

Otra opción es comparar la diferencia absoluta de los radios:

• Si \( d \leq | r_1 - r_2 | \) y \( r_1 < r_2 \), la primera circunferencia está dentro de la segunda.
• Si \( d \leq | r_1 - r_2 | \) y \( r_1 > r_2 \), la segunda circunferencia está dentro de la primera.

Ejemplo

Consideremos las circunferencias:

$$ C_1: x^2 + y^2 + 4x + 6y - 3 = 0 $$

$$ C_2: x^2 + y^2 + 2x + 3y - 1 = 0 $$

Llevemos ambas ecuaciones a forma canónica.

Para \( C_1: x^2 + y^2 + 4x + 6y - 3 = 0 \):

$$ x^2 + 4x + y^2 + 6y = 3 $$

$$ (x^2 + 4x + 4) + (y^2 + 6y + 9) = 3 + 4 + 9 $$

$$ (x + 2)^2 + (y + 3)^2 = 16 $$

Así, el centro de \( C_1 \) es $$ (-2, -3) $$

y su radio es $$ r_1 = \sqrt{16} = 4 $$

Explicación: Para completar el cuadrado en $ x^2 + 4x $, sumamos $ +4 $ a ambos lados. Así, $ x^2 + 4x + 4 = (x+2)^2 $. Lo mismo ocurre en $ y^2 + 6y $, donde añadimos $ +9 $ para obtener $ y^2 + 6y + 9 = (y+3)^2 $.

Para \( C_2: x^2 + y^2 + 2x + 3y - 1 = 0 \):

$$ x^2 + 2x + y^2 + 3y = 1 $$

$$ (x^2 + 2x + 1) + \left(y^2 + 3y + \frac{9}{4}\right) = 1 + 1 + \frac{9}{4} $$

$$ (x + 1)^2 + \left(y + \frac{3}{2}\right)^2 = \frac{17}{4} $$

Por tanto, el centro de \( C_2 \) es $$ (-1, -\frac{3}{2}) $$

y su radio es:

$$ r_2 = \sqrt{\frac{17}{4}} = \frac{\sqrt{17}}{2} \approx 2.06 $$

Con centros en \((-2, -3)\) y \((-1, -\frac{3}{2})\), y radios \( r_1 = 4 \) y \( r_2 = 2.06 \), calculamos la distancia entre los centros y la comparamos con la diferencia absoluta de los radios:

$$ d < | r_1 - r_2 | $$

La distancia \( d \) entre \((-2, -3)\) y \((-1, -\frac{3}{2})\) es:

$$ d = \sqrt{(x_1 + x_2)^2 + (y_1 + y_2)^2} $$

$$ d = \sqrt{(-2 + 1)^2 + \left(-3 + \frac{3}{2}\right)^2} $$

$$ d = \sqrt{(-1)^2 + \left(-\frac{3}{2}\right)^2} $$

$$ d = \sqrt{1 + \frac{9}{4}} $$

$$ d = \sqrt{\frac{13}{4}} $$

$$ d = \frac{\sqrt{13}}{2} \approx 1.8 $$

Comprobamos si una circunferencia está dentro de la otra:

$$ d < | r_1 - r_2 | $$

$$ 1.8 < | 4 - 2.06 | $$

$$ 1.8 < 1.94 $$

Esto confirma que una circunferencia está contenida en la otra.

Dado que \( r_2 < r_1 \), concluimos que la segunda circunferencia \( C_2 \) está contenida dentro de la primera \( C_1 \).

Por tanto, \( C_2 \) está dentro de \( C_1 \).

Circunferencias concéntricas en geometría analítica

Dos circunferencias se denominan concéntricas cuando comparten el mismo centro, aunque tienen radios distintos. En geometría analítica, esto implica que las ecuaciones de ambas circunferencias presentan los mismos coeficientes $ a = a' $ y $ b = b' $ en los términos que afectan a \( x \) y \( y \), pero difieren en el término constante $ c \ne c' $.

Consideremos las ecuaciones generales de dos circunferencias:

$$ C_1 : x^2 + y^2 + ax + by + c = 0 $$

$$ C_2: x^2 + y^2 + a'x + b'y + c' = 0 $$

Si ambas circunferencias son concéntricas, necesariamente comparten el mismo centro.

Esto significa que los términos que incluyen \( x \) y \( y \) —es decir, \( ax = a'x \) y \( by = b'y \)— deben coincidir en las dos ecuaciones.

Por tanto, los coeficientes \( a \) y \( b \) deben ser iguales:

$$ a = a' $$

$$ b = b' $$

La única diferencia entre dos circunferencias concéntricas radica en el término constante \( c \), que determina la diferencia entre sus radios. En consecuencia, \( c \neq c' \).

$$ c \neq c' $$

Nota: Si las ecuaciones de ambas circunferencias tienen los mismos coeficientes $ a = a' $, $ b = b' $ y también $ c = c' $, entonces se trata de circunferencias coincidentes, es decir, comparten el mismo centro y el mismo radio.

Ejemplo práctico

Veamos un ejercicio con las siguientes circunferencias:

$$ C_1 : x^2 + y^2 + 4x + 6y - 3 = 0 $$

$$ C_2: x^2 + y^2 + 4x + 6y - 8 = 0 $$

Ambas circunferencias tienen su centro en \( \left(-2, -3\right) \), ya que los coeficientes de \( x \) y \( y \) coinciden.

$$ (x_0, y_0) = \left( - \frac{a}{2}, -\frac{b}{2} \right) = \left( - \frac{4}{2}, -\frac{6}{2} \right) = (-2, -3) $$

La fórmula para calcular el radio de una circunferencia es:

$$ r = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2 - c} $$

Así, los radios de ambas circunferencias se calculan del siguiente modo:

• Para la primera circunferencia: $$ r_1 = \sqrt{(-2)^2 + (-3)^2 + 3} = \sqrt{4 + 9 + 3} = \sqrt{16} = 4 $$
• Para la segunda circunferencia: $$ r_2 = \sqrt{(-2)^2 + (-3)^2 + 8} = \sqrt{4 + 9 + 8} = \sqrt{21} \approx 4.58 $$

La distancia entre sus centros es cero \( d = 0 \), puesto que son concéntricas. Sin embargo, al tener radios distintos, no son circunferencias coincidentes.

$$ d < | r_1 - r_2 | $$

$$ 0 < | 4 - 4.58 | $$

$$ 0 < 0.58 $$

Esto confirma que una circunferencia está contenida dentro de la otra.

Comparando los radios \( r_1 = 4 \) y \( r_2 \approx 4.58 \), concluimos que la circunferencia \( C_1 \), cuyo radio es menor, está completamente contenida dentro de la circunferencia \( C_2 \), que posee un radio ligeramente mayor.

 

Y así sucesivamente.