Principio de Proporcionalidad entre Circunferencias
Las longitudes de las circunferencias son directamente proporcionales a sus radios, lo que se expresa mediante la relación $$ c:c' = r:r' $$
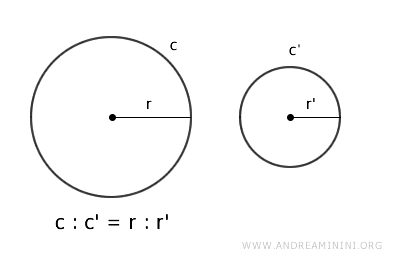
En otras palabras, al comparar dos circunferencias cualesquiera, la razón entre sus longitudes coincide con la razón entre sus radios.
$$ \frac{c}{c'} = \frac{r}{r'} $$
En esta fórmula, c y c' representan las longitudes de las circunferencias, mientras que r y r' son sus respectivos radios.
Nota: Este principio revela una relación esencial entre la longitud de una circunferencia y su radio, y pone de manifiesto la importancia de la constante que conocemos como "pi" (π=3.1415…), que expresa precisamente la razón entre la longitud de la circunferencia y su diámetro (es decir, el doble del radio).
Demostración del Principio
Consideremos dos circunferencias cuyas longitudes sean c y c', y cuyos radios sean r y r'.
Para ilustrar el principio, podemos inscribir polígonos regulares, como hexágonos, en el interior de cada circunferencia.
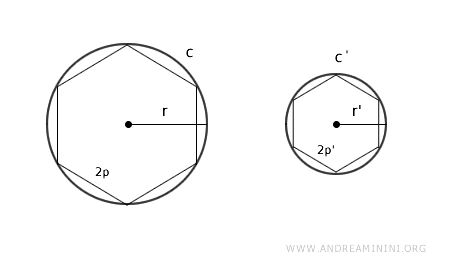
Al ser polígonos regulares, y por tanto semejantes, sus perímetros y lados guardan siempre la misma proporción.
Además, un teorema sobre polígonos regulares establece que los radios de las circunferencias que los inscriben o circunscriben son igualmente proporcionales.
Esto nos permite expresar la relación:
$$ 2p : 2p' = r : r' $$
Donde 2p es el perímetro (y p el semiperímetro) del polígono regular inscrito, y r es el radio de la circunferencia.
Así, la razón de proporcionalidad se mantiene constante:
$$ k = \frac{2p}{2p'} = \frac{r}{r'} $$
Si trasladamos este razonamiento a los polígonos regulares circunscritos alrededor de la circunferencia, el principio sigue cumpliéndose.
Por ejemplo, si volvemos a utilizar hexágonos, pero esta vez circunscritos, obtenemos:
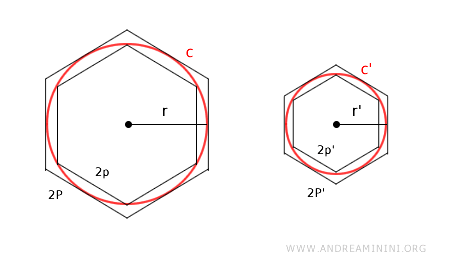
Al ser polígonos regulares y semejantes, sus perímetros, sus lados y los radios de las circunferencias correspondientes mantienen la misma proporción.
$$ 2P : 2P' = r : r' $$
Siendo 2P el perímetro (y P el semiperímetro) del polígono regular circunscrito, y r el radio de la circunferencia.
Como el perímetro del polígono circunscrito siempre es mayor que el del inscrito, se deduce:
$$ 2p < c < 2P $$
Es decir, la longitud de la circunferencia (c) está comprendida entre los perímetros de los polígonos inscrito y circunscrito.
Si aplicamos la misma razón de proporcionalidad k a estas relaciones:
$$ 2p \cdot k < c \cdot k < 2P \cdot k $$
Y dado que 2p' = 2p · k y 2P' = 2P · k, concluimos:
$$ 2p' < c' < 2P' $$
Por lo tanto, existe una relación de proporcionalidad que rige las longitudes de las dos circunferencias, reflejando exactamente la misma proporción que se observa en los polígonos regulares inscritos y circunscritos.
$$ c' = c \cdot k $$
O, de forma equivalente:
$$ k = \frac{c}{c'} $$
Siendo k, además, la razón entre los radios de ambas circunferencias:
$$ k = \frac{c}{c'} = \frac{r}{r'} $$
Lo que confirma la proporción:
$$ c : c' = r : r' $$
Queda así demostrada la proporcionalidad directa entre las longitudes de las circunferencias y sus radios.
Este razonamiento se extiende igualmente a la relación entre circunferencias y diámetros, dado que el diámetro es el doble del radio:
$$ c : c' = 2 \cdot r : 2 \cdot r' $$
$$ c : c' = d : d' $$
Reordenando los términos medios, se obtiene:
$$ c : d = c' : d' $$
En conclusión, la razón entre la longitud de una circunferencia (c) y su diámetro (d) permanece constante, sin importar el tamaño de la circunferencia, y corresponde precisamente a la constante conocida como "pi" (π), cuyo valor es 3.141592…
Y eso es todo.