Haz de Circunferencias

Un haz de circunferencias es un conjunto de circunferencias que comparten ciertas propiedades geométricas.
ejemplo de haz de circunferencias

Existen principalmente dos tipos: haz propio y haz impropio.

Haz propio
Todas las circunferencias del haz pasan por dos puntos fijos denominados puntos base. La ecuación general de un haz propio es $ \lambda (x^2 + y^2) + \mu (Ax + By + C) = 0 $, donde $ \lambda $ y $ \mu $ son parámetros reales.
Haz impropio
Todas las circunferencias tienen el mismo centro y difieren únicamente en el radio. La ecuación de un haz impropio es $ (x - h)^2 + (y - k)^2 = r^2 $, donde $ (h, k) $ es el centro común y $ r $ es variable.

Haz de Circunferencias a partir de Dos Circunferencias Generadoras

Un haz de circunferencias está formado por el conjunto de todas las circunferencias obtenidas como combinación lineal de dos circunferencias generadoras:

$$ (x^2 + y^2 + ax + by + c) + k \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$

donde $ k $ es un parámetro real.

Al variar el valor de $ k $, se generan todas las circunferencias del haz, salvo la segunda circunferencia generadora, que no puede reproducirse exactamente mediante ningún valor de $ k $.

Sin embargo, hay dos casos particulares que conviene destacar:

Si k = 0, se obtiene la primera circunferencia: $$ (x^2 + y^2 + ax + by + c) + 0 \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$ $$ x^2 + y^2 + ax + by + c = 0 $$
Si k = -1, se obtiene una recta conocida como el eje radical del haz de circunferencias: $$ (x^2 + y^2 + ax + by + c) + (-1) \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$ $$ \require{cancel} \cancel{x^2} + \cancel{y^2} + ax + by + c - \cancel{x^2} - \cancel{y^2} - a'x - b'y - c' = 0 $$ $$ (a - a')x + (b - b')y + (c - c') = 0 $$

Nota: El eje radical de un haz de circunferencias puede interpretarse como una “circunferencia degenerada”, ya que corresponde conceptualmente a una circunferencia de radio infinito.

El eje radical de un haz puede o no intersectar a las dos circunferencias generadoras:

Si las circunferencias generadoras se cortan en dos puntos A y B (llamados puntos base del haz), el eje radical pasa por esos dos puntos.
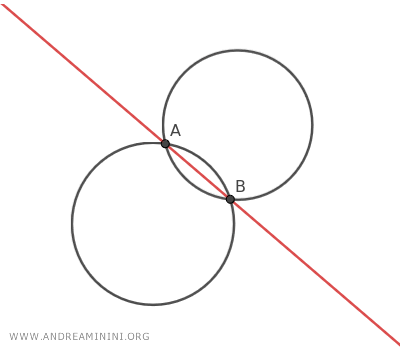
Si las circunferencias generadoras son tangentes en un único punto base A, el eje radical pasa por el punto de tangencia.
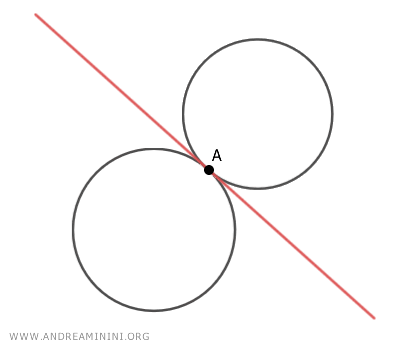
Si las circunferencias generadoras son exteriores (es decir, no tienen puntos en común), el eje radical se ubica en la zona exterior entre ambas circunferencias.

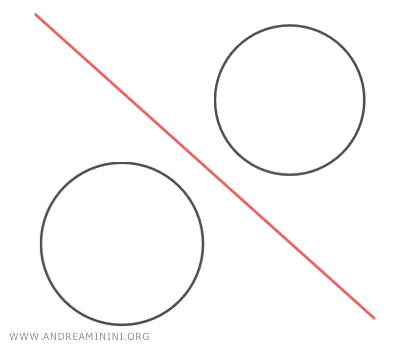
El conjunto de todos los centros de las circunferencias generadas por un haz forma una recta perpendicular al eje radical, conocida como el eje central del haz.

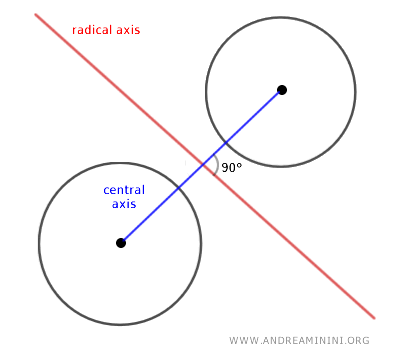
el eje central

Nota: En el caso particular en el que se cumplen $ a = a' $ y $ b = b' $, las circunferencias generadoras son concéntricas. En tal caso, el haz está formado exclusivamente por circunferencias concéntricas y el eje radical no existe.
caso de circunferencias generadoras concéntricas

Ejemplo

Consideremos las siguientes circunferencias generadoras:

$$ C_1 : \ x^2 + y^2 + 2x + 3y - 5 = 0 $$

$$ C_2 : \ x^2 + y^2 - 4x - 4y + 1 = 0 $$

Estas dos circunferencias se cortan en dos puntos base A y B.

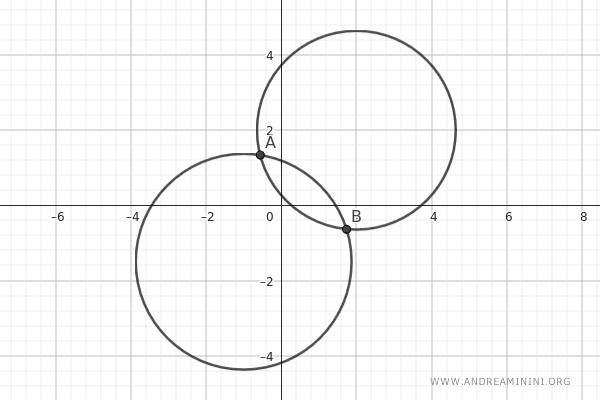
las circunferencias generadoras

Esto significa que todas las circunferencias del haz pasarán por esos dos puntos A y B.

La ecuación del haz formado por estas dos circunferencias es:

$$ C_1 + k \cdot C_2 = 0 $$

$$ (x^2 + y^2 + 2x + 3y - 5) + k \cdot (x^2 + y^2 - 4x - 4y + 1) = 0 $$

Al variar el parámetro $ k $, se obtienen todas las circunferencias del haz.

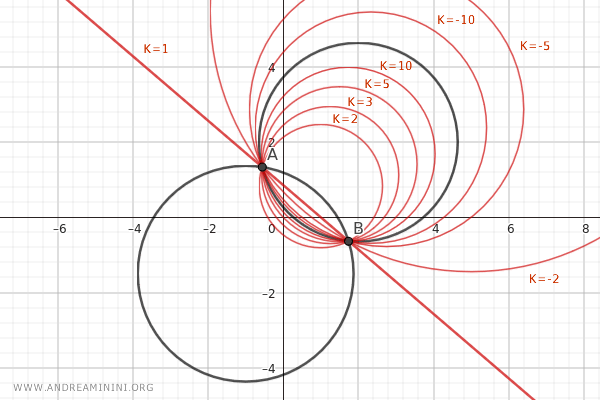
el haz de circunferencias

Si $ k = 0 $, se obtiene la circunferencia $ C_1 $:

$$ (x^2 + y^2 + 2x + 3y - 5) + 0 \cdot (x^2 + y^2 - 4x - 4y + 1) = 0 $$

$$ x^2 + y^2 + 2x + 3y - 5 = 0 $$

Si $ k = -1 $, se obtiene el eje radical del haz, que pasa por los puntos base A y B:

$$ (x^2 + y^2 + 2x + 3y - 5) + (-1) \cdot (x^2 + y^2 - 4x - 4y + 1) = 0 $$

$$ \require{cancel} \cancel{x^2} + \cancel{y^2} + 2x + 3y - 5 - \cancel{x^2} - \cancel{y^2} + 4x + 4y - 1 = 0 $$

$$ (2 + 4)x + (3 + 4)y - 5 - 1 = 0 $$

$$ 6x + 7y - 6 = 0 $$

El eje central de un haz de circunferencias es la recta que contiene los centros de todas las circunferencias del haz y es perpendicular al eje radical.

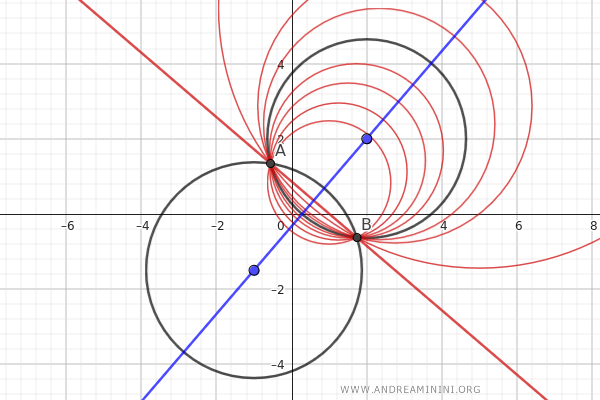
eje central del haz

La Demostración

Consideremos dos circunferencias generadoras:

$$ C_1 = x^2 + y^2 + ax + by + c = 0 $$

$$ C_2 = x^2 + y^2 + a'x + b'y + c' = 0 $$

Realicemos la combinación lineal de ambas ecuaciones, donde $ h $ y $ j $ son números reales cualesquiera:

$$ h \cdot C_1 + j \cdot C_2 = 0 $$

$$ h \cdot (x^2 + y^2 + ax + by + c) + j \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$

Esta ecuación permite obtener todas las circunferencias del haz al variar los coeficientes $ h $ y $ j $.

Nota: Si $ h = 0 $ y $ j = 1 $, se obtiene la ecuación $ C_2 $. En cambio, si $ h = 1 $ y $ j = 0 $, se obtiene la circunferencia $ C_1 $.

Dividimos toda la ecuación entre $ h $:

$$ \frac{1}{h} \cdot [ h \cdot (x^2 + y^2 + ax + by + c) + j \cdot (x^2 + y^2 + a'x + b'y + c') ] = 0 \cdot \frac{1}{h} $$

$$ (x^2 + y^2 + ax + by + c) + \frac{j}{h} \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$

Llamemos $ k $ a la razón $ j/h $:

$$ (x^2 + y^2 + ax + by + c) + k \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$

De esta manera, al variar $ k $, se pueden obtener todas las circunferencias del haz, excepto la circunferencia $ C_2 $.

Nota: Si $ k = 0 $, se obtiene la ecuación de $ C_1 $. En esta forma del haz, no existe ningún valor de $ k $ que reproduzca exactamente la circunferencia $ C_2 $.

Y así sucesivamente.