Cómo calcular el radio de una circunferencia
Para determinar el radio de una circunferencia a partir de su ecuación en forma general $$ x^2 + y^2 + Dx + Ey + F = 0 $$, se emplea la siguiente fórmula: $$ r = \sqrt{\left(-\frac{D}{2}\right)^2 + \left(-\frac{E}{2}\right)^2 - F } $$
Si la ecuación de la circunferencia está expresada en forma ordinaria, calcular el radio es mucho más sencillo.
\[ (x - h)^2 + (y - k)^2 = r^2 \]
En este caso, el centro y el radio de la circunferencia se determinan fácilmente:
- \( (h, k) \) son las coordenadas del centro de la circunferencia.
- \( r \) es el radio de la circunferencia.
Cuando la ecuación se encuentra en forma general:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
El centro \((h, k)\) se obtiene aplicando las siguientes expresiones:
$$ h = -\frac{D}{2} $$
$$ k = -\frac{E}{2} $$
donde \( D \) y \( E \) son los coeficientes de los términos en \( x \) y \( y \) de la ecuación general \( x^2 + y^2 + Dx + Ey + F = 0 \).
Por tanto, el centro de la circunferencia se encuentra en las coordenadas \((-D/2, -E/2)\).
El radio de la circunferencia se calcula mediante la fórmula:
$$ r = \sqrt{\left(-\frac{D}{2}\right)^2 + \left(-\frac{E}{2}\right)^2 - F } $$
Otra forma de determinar el radio y el centro de la circunferencia consiste en transformar la ecuación de forma general a forma ordinaria, completando cuadrados y ajustando los términos necesarios. En la forma ordinaria \( (x - h)^2 + (y - k)^2 = r^2 \), el radio se obtiene directamente calculando \( r = \sqrt{r^2} \).
Ejemplo práctico
Ejemplo 1
En este caso, la ecuación de la circunferencia está dada en forma ordinaria:
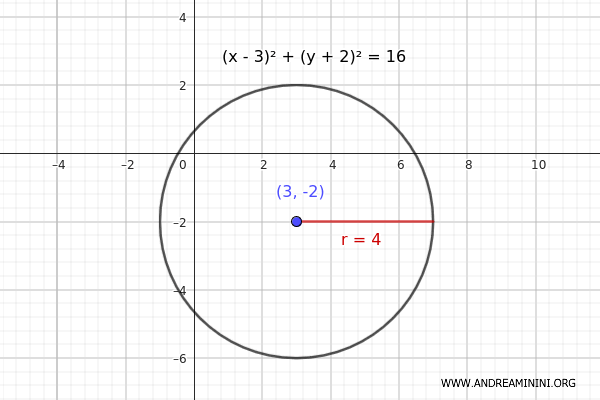
$$ (x - 3)^2 + (y + 2)^2 = 16 $$
Calcular el centro y el radio es inmediato.
- El centro de la circunferencia es \( (3, -2) \).
- El término en el lado derecho es \( r^2 = 16 \).
Para hallar el radio \( r \), basta con extraer la raíz cuadrada positiva de 16:
$$ r = \sqrt{16} = 4 $$
Por tanto, el radio de la circunferencia es 4.
Ejemplo 2
En este segundo caso, la ecuación de la circunferencia no se encuentra en forma ordinaria:
$$ x^2 + y^2 + 6x - 8y + 9 = 0 $$
Podemos determinar el radio empleando directamente la fórmula:
$$ r = \sqrt{\left(-\frac{D}{2}\right)^2 + \left(-\frac{E}{2}\right)^2 - F } $$
donde los coeficientes en la ecuación general \( x^2 + y^2 + Dx + Ey + F = 0 \) son D = 6, E = -8 y F = 9.
$$ r = \sqrt{\left(-\frac{6}{2}\right)^2 + \left(-\frac{-8}{2}\right)^2 - 9 } $$
$$ r = \sqrt{(-3)^2 + (4)^2 - 9 } $$
$$ r = \sqrt{9 + 16 - 9 } $$
$$ r = \sqrt{16 } $$
$$ r = 4 $$
Otra alternativa para hallar el radio es transformar la ecuación de forma general a forma ordinaria.
Agrupamos los términos en \( x \) y \( y \):
$$ x^2 + y^2 + 6x - 8y + 9 = 0 $$
$$ (x^2 + 6x) + (y^2 - 8y) = -9 $$
Completamos el cuadrado para \( x \), sumando y restando \( \left(\frac{6}{2}\right)^2 \):
$$ (x^2 + 6x + \left(\frac{6}{2}\right)^2) - \left(\frac{6}{2}\right)^2 + (y^2 - 8y) = -9 $$
$$ (x^2 + 6x + 3^2) - 9 + (y^2 - 8y) = -9 $$
$$ (x + 3)^2 - 9 + (y^2 - 8y) = -9 $$
$$ (x + 3)^2 + (y^2 - 8y) = 0 $$
Completamos el cuadrado para \( y \), sumando y restando \( \left(\frac{8}{2}\right)^2 \):
$$ (x + 3)^2 + \big(y^2 - 8y + \left(\frac{8}{2}\right)^2\big) - \left(\frac{8}{2}\right)^2 = 0 $$
$$ (x + 3)^2 + (y^2 - 8y + 4^2) - 16 = 0 $$
$$ (x + 3)^2 + (y - 4)^2 = 16 $$
Así, obtenemos la ecuación en forma ordinaria, con \( r^2 = 16 \).
Para calcular el radio, basta tomar la raíz cuadrada de dicho valor:
$$ r = \sqrt{16} = 4 $$
Por tanto, el radio de la circunferencia es 4.
Otras fórmulas útiles para calcular el radio
En general, la fórmula que se utiliza para hallar el radio \( r \) de una circunferencia depende de la información de la que dispongamos.
Algunos casos frecuentes son los siguientes:
- Si se conoce la longitud de la circunferencia: $$ r = \frac{C}{2\pi} $$ donde \( C \) es la longitud de la circunferencia.
- Si se conoce el área: $$ r = \sqrt{\frac{A}{\pi}} $$ donde \( A \) es el área de la circunferencia.
- Si se conocen las coordenadas de los extremos \( (x_1, y_1) \) y \( (x_2, y_2) \) de un diámetro, el radio es la mitad de la distancia euclidiana entre estos puntos: $$ r = \frac{\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}}{2} $$
Estas fórmulas permiten calcular el radio de una circunferencia en distintas situaciones. Se incluyen aquí para ofrecer una visión completa.
Y así concluye la explicación.