Teorema de la Recta Perpendicular al Radio y Tangente a una Circunferencia
Una recta tangente a una circunferencia es perpendicular a su radio, y viceversa.
Consideremos una circunferencia con centro O y radio OP; la recta tangente en el punto P es perpendicular al radio.
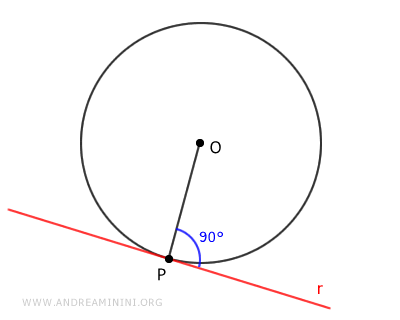
También se cumple el recíproco: si una recta es perpendicular al radio en el punto P de una circunferencia, entonces es tangente a la circunferencia en dicho punto P.
Nota. Esto se debe a que por un punto dado P solo pasa una única perpendicular a una recta, y la distancia más corta entre un punto y una recta siempre se mide a lo largo de la perpendicular. Por lo tanto, la recta tangente en el punto P de la circunferencia es única.
Demostración
La demostración se divide en dos partes: una para el teorema y otra para su recíproco.
A] Una Recta Tangente en un Punto de la Circunferencia es Perpendicular al Radio
Primero, vamos a demostrar que una recta tangente a una circunferencia es perpendicular a su radio.
Consideremos una circunferencia con centro O y radio OP, y una recta tangente en el punto P de la circunferencia.
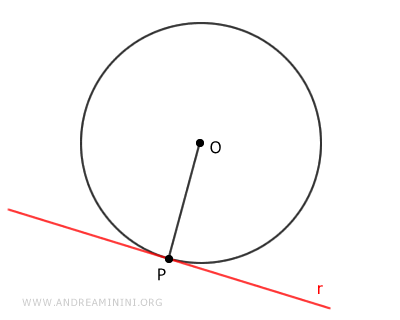
Por definición, una recta tangente tiene un único punto en común con la circunferencia.
Sabemos que por un punto de una recta solo pasa una perpendicular, de modo que deducimos que la tangente posee una única perpendicular en el punto P.
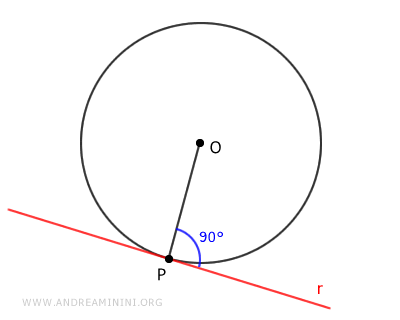
Según el teorema de la distancia de una recta al centro de una circunferencia, una recta es tangente a la circunferencia en el punto P cuando la distancia entre la recta (r) y el centro (O) de la circunferencia es exactamente igual al radio (OP).
$$ d(r,O) \cong \overline{OP} $$
Como la distancia mínima entre una recta y un punto (O) siempre se mide mediante un segmento perpendicular a la recta, formando un ángulo recto (90°), se deduce que el radio es perpendicular a la recta tangente.
$$ \overline{OP} \perp r $$
Además, se concluye que existe una única recta tangente en el punto P.
B] Una Recta Perpendicular al Radio en un Punto de la Circunferencia es Tangente a la Circunferencia
Consideremos una circunferencia con centro O y radio OP.
Supongamos que una recta pasa por el punto P y es perpendicular al radio OP.
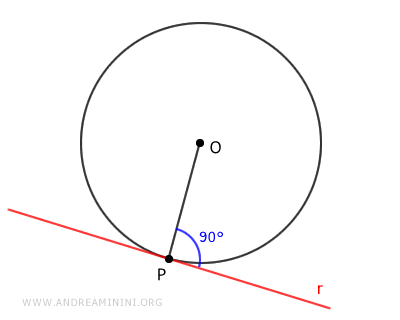
Dado que por un punto dado pasa una única perpendicular a una recta, deducimos que no existe ninguna otra recta diferente en el punto P que cumpla esa condición.
La distancia más corta entre una recta y cualquier punto (O) es siempre un segmento perpendicular (90°) a la recta.
Por lo tanto, el segmento OP mide tanto la distancia entre la recta r y el punto O como el radio.
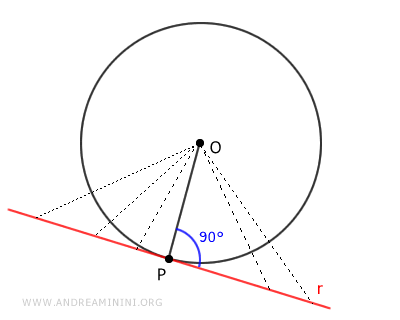
De acuerdo con el teorema de la distancia, si la distancia entre una recta y el centro de la circunferencia coincide exactamente con el radio, la recta corta la circunferencia en un único punto, lo cual significa que es tangente.
Por tanto, la recta perpendicular al radio OP en su extremo P es también tangente a la circunferencia en ese mismo punto P.
Cómo Verificar Matemáticamente que una Recta Tangente es Perpendicular al Radio
Para comprobar matemáticamente que una recta tangente a una circunferencia es perpendicular al radio en el punto de tangencia, podemos recurrir a la geometría analítica.
Veámoslo con un ejemplo concreto.
Consideremos una circunferencia con centro en \( O(0, 0) \) y radio \( r = 5 \). Su ecuación es:
$$ x^2 + y^2 = 25 $$
Supongamos que la ecuación de la recta tangente es:
$$ y = 3x + c $$
o, de forma equivalente:
$$ 3x - y + c = 0 $$
Para determinar el punto de tangencia, empleamos la condición de que la distancia desde el centro de la circunferencia hasta la recta tangente debe ser igual al radio \( r = 5 \):
$$ d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} = r $$
$$ \frac{|3 \cdot 0 + (-1) \cdot 0 + c|}{\sqrt{3^2 + (-1)^2}} = 5 $$
$$ \frac{|c|}{\sqrt{9 + 1}} = 5 $$
$$ \frac{|c|}{\sqrt{10}} = 5 $$
Despejando obtenemos:
$$ \frac{|c|}{\sqrt{10}} = 5 \quad \Rightarrow \quad |c| = 5\sqrt{10} $$
Por tanto, \( c = 5\sqrt{10} \) o \( c = -5\sqrt{10} \).
Si elegimos, por ejemplo, \( c = 5\sqrt{10} \), la ecuación de la recta tangente será:
$$ y = 3x + 5\sqrt{10} $$
Para verificarlo gráficamente, podemos representar la circunferencia y la recta tangente:
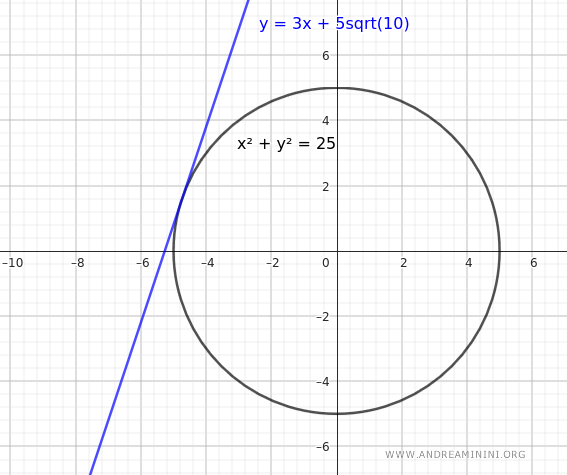
El punto de tangencia \( T(x_1, y_1) \) debe satisfacer ambas ecuaciones:
$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1^2 + y_1^2 = 25 \end{cases} $$
Sustituyendo \( y_1 \) en la ecuación de la circunferencia:
$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1^2 + (3x_1 + 5\sqrt{10})^2 = 25 \end{cases} $$
$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1^2 + 9x_1^2 + 30\sqrt{10}x_1 + 250 = 25 \end{cases} $$
$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ 10x_1^2 + 30\sqrt{10}x_1 + 225 = 0 \end{cases} $$
Resolviendo esta ecuación cuadrática, obtenemos \( x_1 \), y posteriormente \( y_1 \).
Al resolverla, se obtiene \( x_1 = -1.5\sqrt{10} \approx -4.743 \).
$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1 = -1.5\sqrt{10} \approx -4.743 \end{cases} $$
Nota: Estos son los pasos para calcular \( x_1 \). $$ x_1 = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ donde \( a = 10 \), \( b = 30\sqrt{10} \), \( c = 225 \). $$ x_1 = \frac{-30\sqrt{10} \pm \sqrt{(30\sqrt{10})^2 - 4 \cdot 10 \cdot 225}}{2 \cdot 10} $$ $$ x_1 = \frac{-30\sqrt{10} \pm \sqrt{9000 - 9000}}{20} $$ $$ x_1 = \frac{-30\sqrt{10}}{20} $$ $$ x_1 = -1.5\sqrt{10} \approx -4.743 $$
Sustituyendo \( x_1 = -1.5\sqrt{10} \) (aprox. -4.743) en la primera ecuación, obtenemos \( y_1 = 0.5\sqrt{10} \) (aprox. 1.58):
$$ \begin{cases} y_1 = 3 \cdot (-1.5\sqrt{10}) + 5\sqrt{10} \\ \\ x_1 = -1.5\sqrt{10} \end{cases} $$
$$ \begin{cases} y_1 = -4.5\sqrt{10} + 5\sqrt{10} \\ \\ x_1 = -1.5\sqrt{10} \end{cases} $$
$$ \begin{cases} y_1 = 0.5\sqrt{10} \approx 1.58 \\ \\ x_1 = -1.5\sqrt{10} \approx -4.743 \end{cases} $$
Por lo tanto, el punto de tangencia P se encuentra en las coordenadas (x1, y1) = (-1.5√10, 0.5√10), o aproximadamente (-4.743, 1.58).
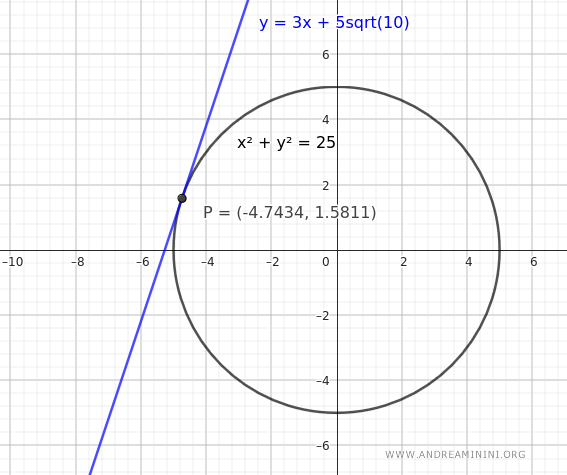
A continuación, hallamos la ecuación del radio que pasa por el centro de la circunferencia \( O(0, 0) \) y por el punto de tangencia P.
La ecuación de una recta que pasa por dos puntos \( (x_1, y_1) \) y \( (x_2, y_2) \) es:
$$ y - y_1 = m (x - x_1) $$
donde \( m \) es la pendiente de la recta, calculada así:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
En nuestro caso, los puntos son \( O(0, 0) \) y \( T(-4.743, 1.58) \).
Así, la pendiente \( m \) resulta ser:
$$ m = \frac{0.5\sqrt{10} - 0}{-1.5\sqrt{10} - 0} = \frac{0.5\sqrt{10}}{-1.5\sqrt{10}} = -\frac{1}{3} \approx -0.333 $$
Podemos escribir la ecuación de la recta que contiene al radio y pasa por el punto de tangencia:
$$ y - 0 = - \frac{1}{3} (x - 0) $$
Así, la ecuación del radio es:
$$ y = - \frac{1}{3} x $$
Para ilustrarlo, añadimos en el gráfico la recta \( y = -\frac{1}{3}x \) (en rojo), que corresponde al radio OP.
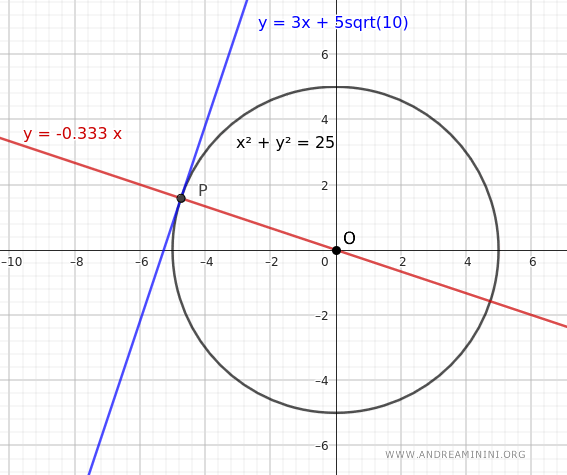
Por último, debemos verificar que el radio es efectivamente perpendicular a la tangente.
Sabemos que dos rectas son perpendiculares si el producto de sus pendientes es igual a \( -1 \). Por lo tanto, debemos comprobar:
$$ m_{\text{radio}} \cdot m_{\text{tangente}} = -1 $$
La pendiente de la tangente es \( 3 \) y la del radio es \( -\frac{1}{3} \).
$$ -\frac{1}{3} \cdot 3 = -1 $$
El resultado es -1, por lo que podemos confirmar que el radio es efectivamente perpendicular a la recta tangente.
Con esto, queda demostrado matemáticamente que cualquier recta tangente es perpendicular al radio en el punto de tangencia.
Y así sucesivamente.