Ángulo Inscrito
Un ángulo inscrito se forma cuando dos rectas, que parten de dos puntos cualesquiera sobre la circunferencia, se encuentran en otro punto de esa misma circunferencia, generando así un ángulo convexo. Estas rectas pueden ambas cortar la circunferencia o bien, una de ellas cortar el círculo mientras la otra es tangente a él.
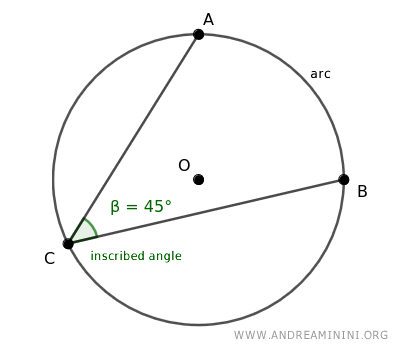
Los lados de este ángulo intersectan la circunferencia en dos puntos distintos, que marcan los extremos de un arco.
Por esta razón, se dice que el ángulo inscrito subtiende el arco; es decir, que el arco está subtenido por el ángulo.
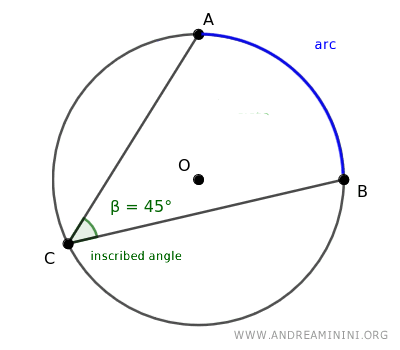
Para cualquier arco AB dado en la circunferencia, es posible construir infinitos ángulos inscritos cuyos lados pasen por los puntos A y B.
Un dato fundamental: todos los ángulos inscritos que subtienden un mismo arco tienen exactamente la misma amplitud.
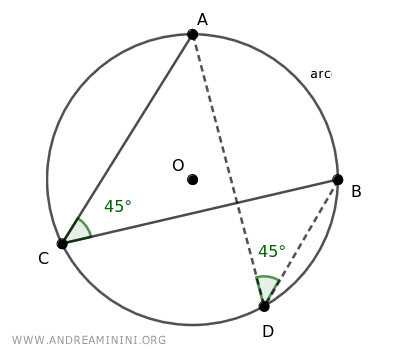
Ejemplo: Consideremos el arco AB y dos ángulos inscritos que lo subtienden. Ambos tendrán la misma medida y, por tanto, son congruentes.
Un ángulo inscrito (β) y un ángulo central (α) se denominan ángulos correspondientes cuando subtienden el mismo arco.
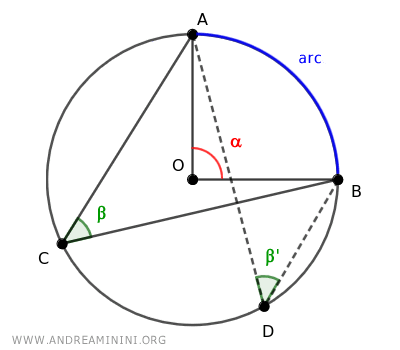
Existe un único ángulo central (α) y una infinidad de ángulos inscritos (β, β') que pueden subtender un mismo arco.
Además, todo ángulo inscrito mide exactamente la mitad del ángulo central que subtiende el mismo arco.
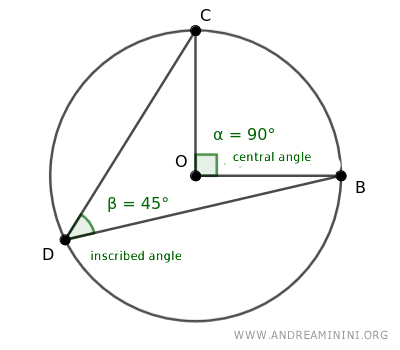
Por lo tanto, todos los ángulos inscritos que subtienden un mismo arco son congruentes (β≅β'), es decir, tienen idéntica medida.
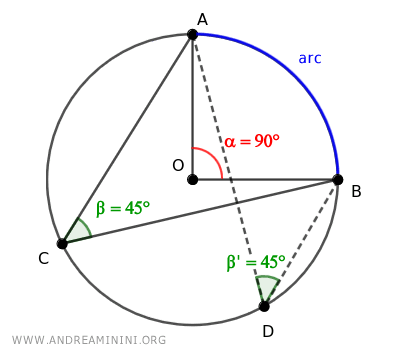
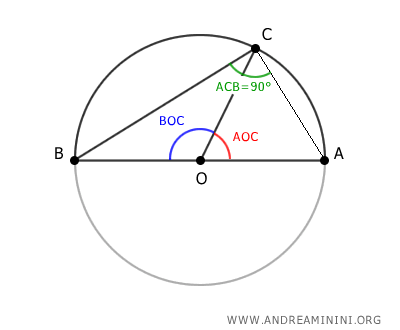
Así, según el Teorema del Ángulo Inscrito, cualquier ángulo inscrito que subtienda una semicircunferencia es, necesariamente, un ángulo recto (90°).
Observaciones
Algunos aspectos adicionales sobre los ángulos inscritos:
- Dado un arco, todos los ángulos inscritos que lo subtienden son congruentes, es decir, poseen la misma amplitud.
- La medida de un ángulo inscrito es siempre la mitad de la medida del arco que subtiende.
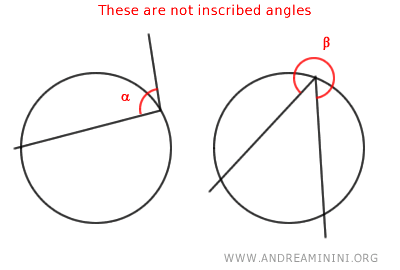
- Excepciones a los ángulos inscritos: No todos los ángulos pueden considerarse inscritos. Por ejemplo, el ángulo α no tiene ninguno de sus lados que corte o sea tangente a la circunferencia, y el ángulo β no es convexo.
Y así sucesivamente.