Intersección de una Recta y una Circunferencia: El Teorema de los Puntos Comunes
Una recta y una circunferencia pueden intersectarse, como máximo, en dos puntos.
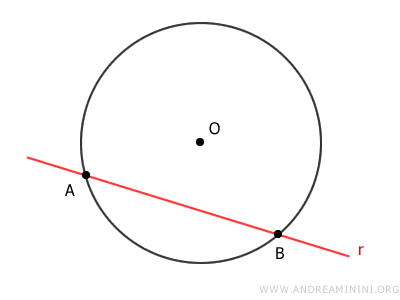
En otras palabras, no pueden existir más de dos puntos comunes en los que una recta corte a una circunferencia.
Se denomina recta secante a aquella que intersecta la circunferencia en dos puntos.
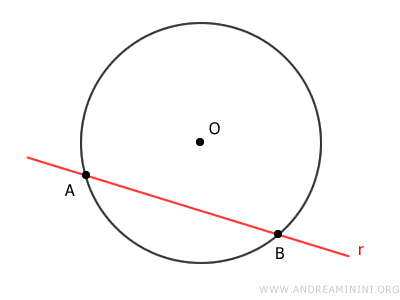
Si la recta corta la circunferencia en un único punto, se la llama recta tangente.
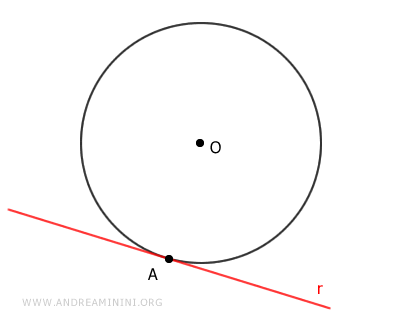
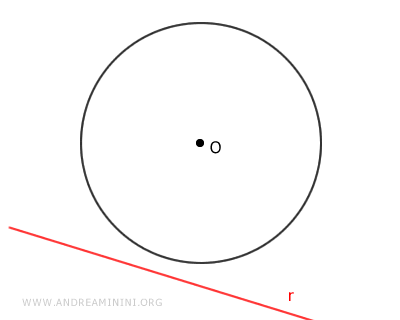
En cambio, si la recta no intersecta la circunferencia en ningún punto, se la denomina recta exterior.
Demostración del Teorema
Veamos una demostración por reducción al absurdo para establecer este teorema.
Supongamos que la recta r y la circunferencia se cortan en tres o más puntos: A, B y C.
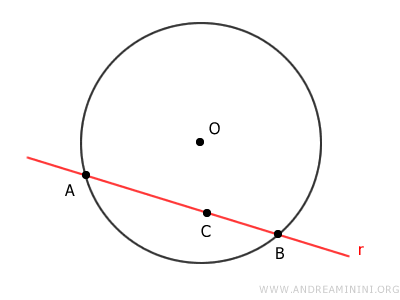
Los puntos A, B y C se encuentran sobre la misma recta r, formando los segmentos consecutivos AB y BC.
Como están alineados, los segmentos AB y BC tienen sus ejes perpendiculares a la recta r y, por tanto, son paralelos entre sí.
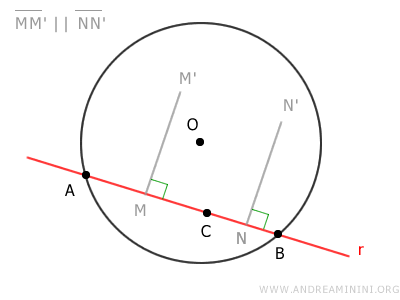
En consecuencia, los ejes MM' y NN' de los segmentos AB y BC son paralelos y no se cortan.
$$ \overline{MM'} \cap \overline{NN'} = \emptyset $$
Sin embargo, los segmentos AB y BC son también cuerdas de la circunferencia, lo que implica que los puntos A, B y C, además de estar sobre la recta, pertenecen también a la circunferencia.
Dado que el eje de cualquier cuerda pasa por el centro de la circunferencia, se deduce que los ejes de las cuerdas AB y BC se intersectan en el punto O.
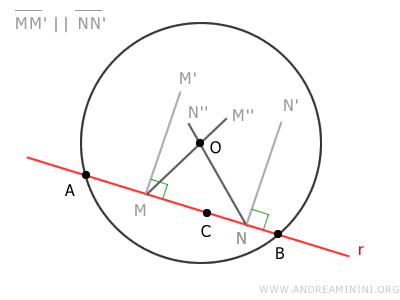
Por lo tanto, los ejes MM' y NN' se cortan en el punto O, lo que contradice la hipótesis de que son paralelos.
$$ \overline{MM'} \cap \overline{NN'} = O $$
Esta contradicción demuestra que una recta y una circunferencia no pueden tener tres puntos comunes.
Nota: Este razonamiento es igualmente válido si se supone que existen cuatro o más puntos de intersección entre la recta y la circunferencia.
Si la hipótesis inicial es falsa, necesariamente debe cumplirse la proposición contraria.
Por tanto, una recta y una circunferencia pueden intersectarse, como máximo, en dos puntos.
Y con esto queda demostrado.