Circunferencias exteriores

Dos circunferencias se consideran exteriores cuando la distancia entre sus centros, indicada como OO', es mayor que la suma de sus radios: $$ \overline{OO'} > r + r' $$. Esto significa que las circunferencias no se tocan ni se solapan en ningún punto.

En este contexto, OO' representa la distancia entre los centros de ambas circunferencias, mientras que $ r $ y $ r' $ corresponden a sus respectivos radios.

Geométricamente, esto implica que cada circunferencia está completamente situada fuera de la otra, sin ningún punto en común.

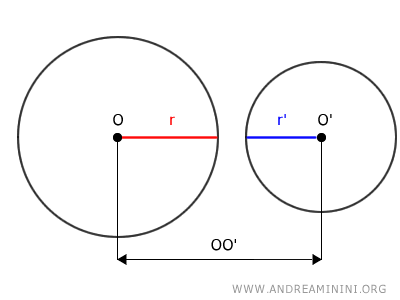
Cuando la distancia OO' es mayor que la suma de los radios $ r + r' $, los centros O y O' se encuentran, cada uno, fuera de la circunferencia de la otra.

Además, la suma del radio y la distancia desde el centro de una circunferencia (O + r y O' + r') no alcanza a cortar la otra circunferencia, lo que garantiza que ambas permanezcan completamente separadas.

Ejemplo práctico

Analicemos si las siguientes circunferencias son exteriores entre sí:

$$ C_1 : x^2 + y^2 - 4x - 8y = -16 $$

$$ C_2 : x^2 + y^2 - 2x + 4y = 2 $$

Primero, reescribimos ambas ecuaciones en su forma canónica $ (x - h)^2 + (y - k)^2 = r^2 $ para identificar el centro $ (h, k) $ y el radio $ r $ de cada circunferencia:

Primera ecuación: $$ x^2 + y^2 - 4x - 8y = -16 $$ Completamos el cuadrado para $ x $ y $ y $: $$ (x^2 - 4x + 4) + (y^2 - 8y + 16) = -16 + 4 + 16 $$ $$ (x - 2)^2 + (y - 4)^2 = 4 $$ Por tanto, la primera circunferencia tiene centro en $(2, 4)$ y radio $ r_1 = \sqrt{4} = 2 $.
Segunda ecuación: $$ x^2 + y^2 - 2x + 4y = 2 $$ Completamos el cuadrado para $ x $ y $ y $: $$ (x^2 - 2x + 1) + (y^2 + 4y + 4) = 2 + 1 + 4 $$ $$ (x - 1)^2 + (y + 2)^2 = 7 $$ Así, la segunda circunferencia tiene centro en $(1, -2)$ y radio $ r_2 = \sqrt{7} \approx 2.65 $.

A continuación, calculamos la distancia entre los centros mediante la fórmula de distancia euclídea:

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

Para la primera circunferencia, $ O_1 = (2, 4) $, es decir, $ x_1 = 2 $ y $ y_1 = 4 $. Para la segunda, $ O_2 = (1, -2) $, por tanto $ x_2 = 1 $ y $ y_2 = -2 $.

$$ d = \sqrt{(1 - 2)^2 + (-2 - 4)^2} $$

$$ d = \sqrt{(-1)^2 + (-6)^2} $$

$$ d = \sqrt{1 + 36} $$

$$ d = \sqrt{37} \approx 6.08 $$

Por último, verificamos si las circunferencias son exteriores.

Son exteriores si la distancia entre sus centros es mayor que la suma de sus radios:

$$ d > r_1 + r_2 $$

$$ 6.08 > 2 + 2.65 $$

$$ 6.08 > 4.65 $$

Dado que $ 6.08 > 4.65 $, concluimos que las dos circunferencias son exteriores y no se intersectan ni se tocan.

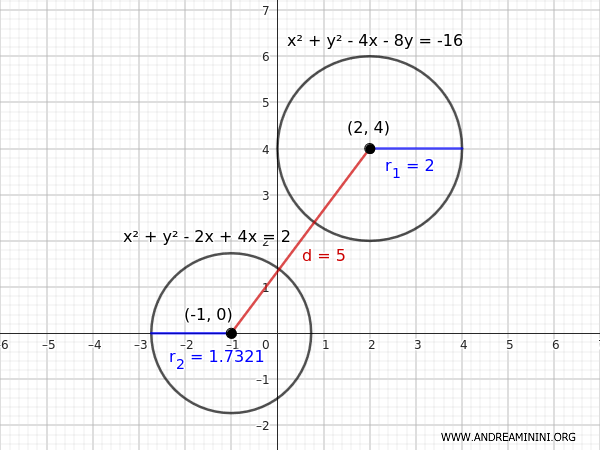
las circunferencias son exteriores

Solución alternativa

Verifiquemos si las siguientes circunferencias son exteriores entre sí:

$$ C_1 : x^2 + y^2 - 4x - 8y = -16 $$

$$ C_2 : x^2 + y^2 - 2x + 4y = 2 $$

Usamos la fórmula para encontrar el centro de una circunferencia $ \left( -\frac{a}{2}, -\frac{b}{2} \right) $, partiendo de la ecuación general $ x^2 + y^2 + ax + by + c = 0 $:

$$ C_1 : x^2 + y^2 - 4x - 8y + 16 = 0 $$

$$ C_2 : x^2 + y^2 - 2x + 4y - 2 = 0 $$

Para la primera circunferencia, los coeficientes son $ a = -4 $ y $ b = -8 $:

$$ O_1 = \left( -\frac{a}{2}, -\frac{b}{2} \right) = \left( -\frac{-4}{2}, -\frac{-8}{2} \right) = (2, 4) $$

Para la segunda, $ a = -2 $ y $ b = 4 $:

$$ O_2 = \left( -\frac{a}{2}, -\frac{b}{2} \right) = \left( -\frac{-2}{2}, -\frac{4}{2} \right) = (1, -2) $$

Para hallar los radios utilizamos la fórmula: $ r = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c} $.

Para la primera circunferencia, con $ a = -4 $, $ b = -8 $, $ c = 16 $:

$$ r_1 = \sqrt{\left(-\frac{-4}{2}\right)^2 + \left(-\frac{-8}{2}\right)^2 - 16} $$

$$ r_1 = \sqrt{2^2 + 4^2 - 16} $$

$$ r_1 = \sqrt{4 + 16 - 16} $$

$$ r_1 = \sqrt{4} $$

$$ r_1 = 2 $$

Para la segunda circunferencia, $ a = -2 $, $ b = 4 $, $ c = -2 $:

$$ r_2 = \sqrt{\left(-\frac{-2}{2}\right)^2 + \left(-\frac{4}{2}\right)^2 - (-2)} $$

$$ r_2 = \sqrt{1^2 + (-2)^2 + 2} $$

$$ r_2 = \sqrt{1 + 4 + 2} $$

$$ r_2 = \sqrt{7} $$

$$ r_2 \approx 2.65 $$

Calculamos nuevamente la distancia euclídea entre los centros:

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

Para $ O_1 = (2, 4) $ y $ O_2 = (1, -2) $: