Teorema de los Ángulos Centrales e Inscritos
En una circunferencia, los ángulos inscritos α tienen una medida igual a la mitad del ángulo central β que abarca el mismo arco AB. $$ \alpha = \frac{1}{2} \beta $$ Ejemplo:
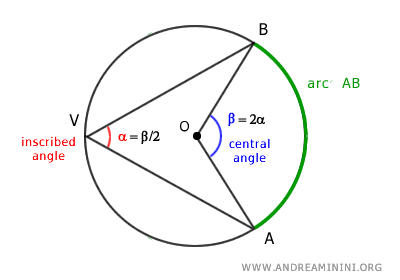
De forma equivalente, podemos afirmar que los ángulos centrales β miden el doble que sus correspondientes ángulos inscritos α.
$$ \beta = 2 \alpha $$
Como solo existe un ángulo central pero infinitos ángulos inscritos que abarcan el mismo arco AB, se concluye que todos los ángulos inscritos α que abarcan el arco AB son congruentes entre sí.
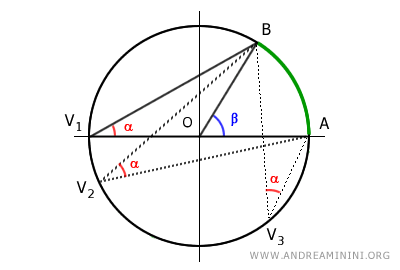
Además, si un ángulo inscrito abarca un semicírculo, es un ángulo recto (90°), ya que en ese caso el ángulo central correspondiente es un ángulo llano (180°).
Demostración
Para probar este teorema, debemos considerar tres casos distintos: cuando el centro de la circunferencia O se sitúa sobre un lado del ángulo inscrito, dentro de él o fuera de él.
A] El centro se encuentra sobre un lado del ángulo inscrito
Si el centro O de la circunferencia está sobre uno de los lados del ángulo inscrito α, ese lado (AV) es un diámetro de la circunferencia.
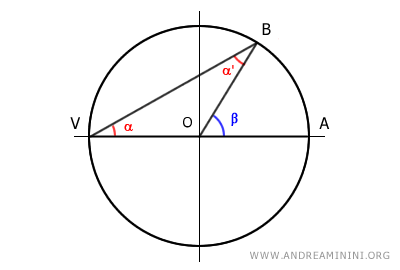
Como AV es un diámetro, su mitad OV corresponde a un radio de la circunferencia.
En este caso, el triángulo VBO es un triángulo isósceles, ya que posee dos lados iguales, los radios OV ≅ OB.
Dado que en un triángulo isósceles los ángulos de la base son congruentes, se deduce que los ángulos α y α' son iguales.
$$ \alpha = \alpha' $$
Según el teorema del ángulo exterior, el ángulo central β es un ángulo exterior del triángulo VBO y equivale a la suma de los dos ángulos interiores no adyacentes α + α'.
$$ \beta = \alpha + \alpha' $$
Como α y α' son congruentes, se tiene α + α' = 2α.
Por tanto, el ángulo central (β) mide el doble que el ángulo inscrito:
$$ \beta = 2 \alpha $$
En consecuencia, el ángulo inscrito (α) mide la mitad del ángulo central:
$$ \alpha = \frac{1}{2} \beta $$
B] El centro está dentro del ángulo inscrito
En este caso, el centro O de la circunferencia se sitúa en el interior del ángulo inscrito α.
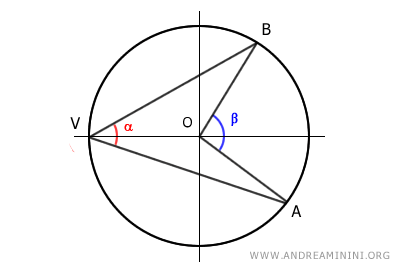
Se traza el diámetro VC, que divide tanto el ángulo inscrito α como el ángulo central β en dos partes.
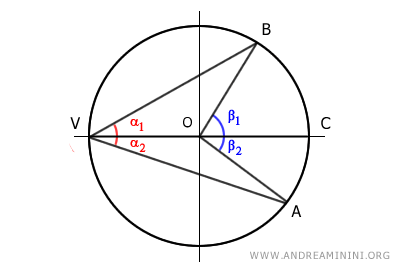
Los ángulos quedan expresados de la siguiente forma:
$$ \alpha = \alpha_1 + \alpha_2 $$
$$ \beta = \beta_1 + \beta_2 $$
Ambos ángulos inscritos α1 y α2 tienen uno de sus lados coincidente con el diámetro de la circunferencia.
En la sección [A] de esta demostración, ya se ha probado que los ángulos inscritos que tienen un lado sobre el diámetro miden la mitad de su ángulo central correspondiente.
Por tanto, los ángulos α1 y α2 valen la mitad de sus ángulos centrales respectivos β1 y β2:
$$ \alpha_1 = \frac{1}{2} \beta_1 $$
$$ \alpha_2 = \frac{1}{2} \beta_2 $$
Como el ángulo inscrito es la suma de esos dos ángulos, se tiene:
$$ \alpha = \alpha_1 + \alpha_2 $$
Sustituyendo α1 = (1/2)β1 y α2 = (1/2)β2, resulta:
$$ \alpha = \frac{1}{2} \beta_1 + \frac{1}{2} \beta_2 $$
$$ \alpha = \frac{1}{2} \cdot ( \beta_1 + \beta_2 ) $$
Como el ángulo central es la suma β = β1 + β2:
$$ \alpha = \frac{1}{2} \cdot \beta $$
Esto demuestra que el ángulo inscrito (α) mide la mitad del ángulo central (β/2).
En consecuencia, el ángulo central (β) mide el doble que el ángulo inscrito:
$$ \beta = 2 \alpha $$
C] El centro está fuera del ángulo inscrito
Por último, consideremos el caso en el que el centro O de la circunferencia se encuentra fuera del ángulo inscrito α.
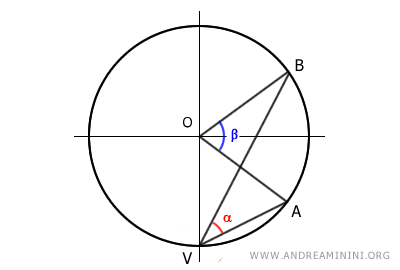
Se traza el diámetro VC para formar dos ángulos adicionales, relacionados con los ángulos α y β por construcción.
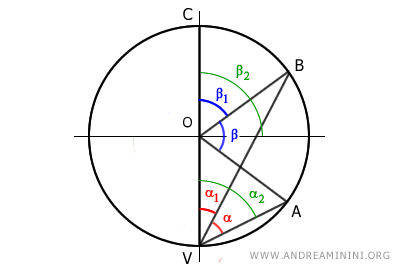
Por construcción, el ángulo inscrito se expresa como α = α2 - α1, mientras que el ángulo central es β = β2 - β1:
$$ \alpha = \alpha_2 - \alpha_1 $$
$$ \beta = \beta_2 - \beta_1 $$
El ángulo α1 es un ángulo inscrito cuyo lado coincide con el diámetro VC, y como se demostró en el apartado [A], mide la mitad del ángulo central β1:
$$ \alpha_1 = \frac{1}{2} \beta_1 $$
El ángulo α2 es también un ángulo inscrito con un lado sobre el diámetro VC, por lo que igualmente mide la mitad de su ángulo central β2:
$$ \alpha_2 = \frac{1}{2} \beta_2 $$
Con α1 = β1/2 y α2 = β2/2, sustituimos en α = α2 - α1:
$$ \alpha = \alpha_2 - \alpha_1 $$
$$ \alpha = \frac{1}{2} \beta_2 - \frac{1}{2} \beta_1 $$
$$ \alpha = \frac{1}{2} \cdot ( \beta_2 - \beta_1 ) $$
Y dado que el ángulo central es la diferencia β = β2 - β1, se concluye que:
$$ \alpha = \frac{1}{2} \cdot \beta $$
Esto demuestra que el ángulo inscrito (α) mide la mitad del ángulo central (β/2).
Por tanto, el ángulo central (β) es el doble del ángulo inscrito:
$$ \beta = 2 \alpha $$
En conclusión, el teorema queda demostrado para todos los casos posibles.
Y así sucesivamente.