Fórmulas de tangentes y rectas polares

Las fórmulas de desdoblamiento permiten expresar las coordenadas de un punto y los parámetros de una curva de manera que se obtenga la ecuación polar.

Para una curva cónica representada en coordenadas cartesianas por la ecuación general:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

y un punto \( P(x_0, y_0) \), la ecuación polar de \( P \) respecto a dicha cónica está dada por:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Trabajamos con curvas cónicas, como circunferencias, elipses, parábolas e hipérbolas, y con puntos situados en el exterior de estas curvas.

El caso más sencillo es el de una circunferencia \( x^2 + y^2 + ax + by + c = 0 \).

El concepto de recta polar surgió en el contexto del desarrollo de la geometría analítica y proyectiva durante el siglo XIX. Matemáticos como Poncelet y Chasles realizaron aportes fundamentales en estas teorías.

Si consideramos una curva cónica, por ejemplo, una circunferencia, y tomamos un punto \( P \) exterior a ella, podemos definir una recta denominada «recta polar» del punto \( P \) respecto a la cónica.

La recta polar es la línea roja que corta la circunferencia en los puntos de tangencia \( A \) y \( B \), que son los puntos en los que las tangentes trazadas desde \( P \) tocan la circunferencia.

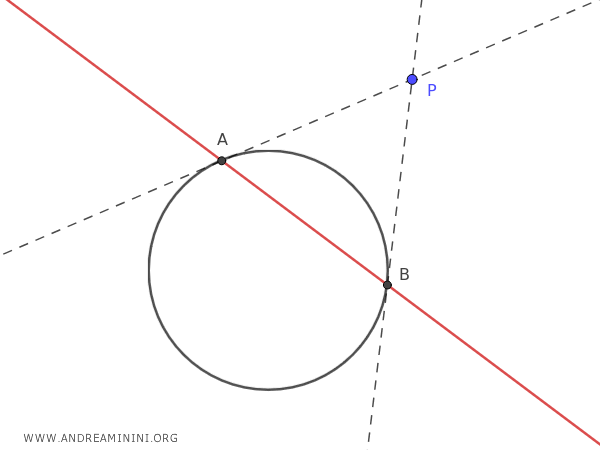
Dicho de otro modo, la recta polar es aquella cuya intersección con la circunferencia coincide con los puntos de tangencia de las tangentes que pasan por el punto exterior \( P \).

En el caso particular en que el punto \( P \) se encuentra sobre la circunferencia, la polar coincide con la tangente en ese punto.

Por tanto, en este caso, se obtiene la ecuación de la tangente.

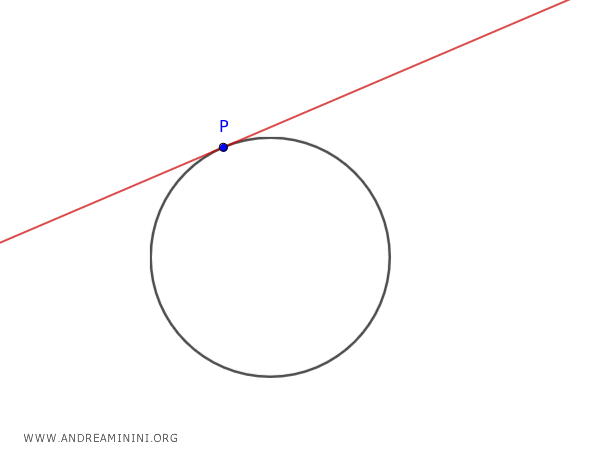
Así, las «fórmulas de desdoblamiento» son ecuaciones que permiten calcular la ecuación de la tangente o de la polar en un punto \( P \) sobre la cónica.

Nota. El término «desdoblamiento» hace referencia a que, al considerar un punto sobre la cónica, podemos interpretarlo como el resultado de la coincidencia de dos puntos de intersección infinitesimalmente próximos en la curva, a partir de los cuales se determina la tangente que toca la cónica en ese punto.

Partiendo de la forma implícita de la cónica, se pueden obtener las siguientes expresiones:

Representación simétrica:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey = 0 $$

Fórmulas de desdoblamiento para cónicas:

Para una circunferencia \( x^2 + y^2 + 2gx + 2fy + c = 0 \):

$$ xx_0 + yy_0 + g(x + x_0) + f(y + y_0) + c = 0 $$

Para una parábola\( y^2 = 4ax \):

$$ yy_0 = 2a(x + x_0) $$

¿Para qué se utilizan? Las fórmulas de desdoblamiento se emplean para hallar las ecuaciones de tangentes, normales y rectas polares asociadas a curvas algebraicas. Por ejemplo, se puede aplicar la fórmula de desdoblamiento a una circunferencia para determinar la ecuación de la tangente en un punto \( P \) de la misma. 

Ejemplo práctico

Veamos un ejemplo práctico para ilustrar el uso de las fórmulas de desdoblamiento y la recta polar.

Consideremos una circunferencia centrada en el origen con radio \( r = 5 \). Su ecuación es:

$$ x^2 + y^2 = 25 $$

Tomemos un punto sobre la circunferencia \( P(3, 4) \).

Nota. Para comprobar que este punto pertenece a la circunferencia, basta sustituir sus coordenadas \( x = 3 \) y \( y = 4 \) en la ecuación: $$ x^2 + y^2 = 25 $$ $$ 3^2 + 4^2 = 25 $$ $$ 9 + 16 = 25 $$ $$ 25 = 25 $$ La igualdad se cumple, lo que confirma que el punto está sobre la circunferencia.

Utilizamos la fórmula \( xx_0 + yy_0 = r^2 \) para hallar la ecuación de la tangente en el punto \( P(3, 4) \).

Sustituyendo \( x_0 = 3 \), \( y_0 = 4 \) y \( r^2 = 25 \) en la ecuación:

$$ x \cdot 3 + y \cdot 4 = 25 $$

$$ 3x + 4y = 25 $$

Esta es la ecuación de la tangente a la circunferencia en el punto \( P(3, 4) \).

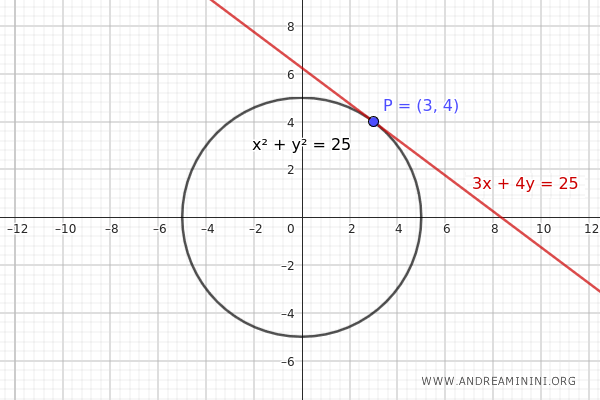
Ahora, vamos a determinar la ecuación de la recta polar respecto a un punto exterior \( Q \) situado fuera de la circunferencia \( x^2 + y^2 = 25 \), por ejemplo \( Q(6, 8) \).

La polar del punto \( Q \) respecto a la circunferencia \( x^2 + y^2 = 25 \) es la recta que contiene todos los puntos de tangencia de las tangentes que pasan por \( Q \).

Usamos nuevamente la fórmula:

$$ xx_0 + yy_0 = r^2 $$

En este caso, \( (x_0, y_0) \) corresponde al punto \( Q(6, 8) \), y la ecuación de la recta polar es:

$$ x \cdot 6 + y \cdot 8 = 25 $$

$$ 6x + 8y = 25 $$

Esta recta es la polar del punto \( Q(6, 8) \) respecto a la circunferencia \( x^2 + y^2 = 25 \).

Los puntos donde la recta polar corta la circunferencia son precisamente los puntos de tangencia \( A \) y \( B \) de las dos tangentes que pasan por el punto exterior \( Q(6, 8) \).

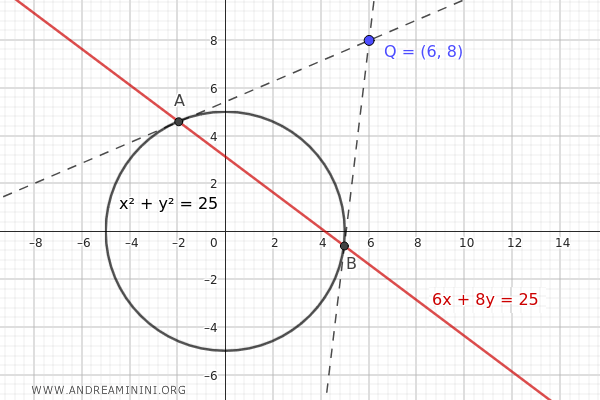
En conclusión, en este ejemplo práctico he utilizado la fórmula de desdoblamiento para hallar la ecuación de la tangente a una circunferencia y para calcular la polar de un punto exterior a ella.

Observaciones

Algunas observaciones y notas sobre las fórmulas de desdoblamiento:

• La polar de un punto respecto a una cónica puede interpretarse como el lugar geométrico de los puntos de tangencia de las tangentes trazadas desde dicho punto a la cónica.
• Si \( P \) es un punto exterior a una cónica, su polar respecto a la cónica es la recta tangente en los puntos de contacto de las tangentes trazadas desde \( P \).
• Si el punto \( P \) se encuentra sobre la polar de \( Q \), entonces \( Q \) se halla sobre la polar de \( P \).

Y así sucesivamente.