Fórmula de la recta tangente a una cónica

La fórmula de la recta tangente (también conocida como regla de desdoblamiento) es un método de la geometría analítica que permite determinar la ecuación de la recta tangente a una cónica en el plano cartesiano, en el punto $ P(x_0, y_0) $. Dicha fórmula es: $$ a_{11}x_0 x + a_{22}y_0 y + a_{12}(x y_0 + x_0 y) + \\ + a_{01}(x + x_0) + a_{02}(y + y_0) + a_{00} = 0 $$ Los coeficientes corresponden a los de la ecuación general de la cónica:
$ a_{11}x^2 + a_{22}y^2 + 2a_{12}xy + 2a_{01}x + 2a_{02}y + a_{00} = 0 $

En otras palabras, esta fórmula permite obtener la recta tangente realizando sustituciones formales sobre los términos de la cónica original, sin necesidad de derivar.

Una sección cónica está dada, en general, por la ecuación:

$$ a_{11}x^2 + a_{22}y^2 + 2a_{12}xy + 2a_{01}x + 2a_{02}y + a_{00} = 0 $$

Según la regla de desdoblamiento, la ecuación de la recta tangente en $ P(x_0, y_0) $ se obtiene mediante las siguientes sustituciones formales:

Para los términos de segundo grado:

$ x^2 \rightarrow x_0 x $
$ y^2 \rightarrow y_0 y $
$ xy \rightarrow \frac{1}{2}(x y_0 + x_0 y) $

Para los términos de primer grado:

$ x \rightarrow \frac{1}{2}(x + x_0) $
$ y \rightarrow \frac{1}{2}(y + y_0) $

Al aplicar estas sustituciones a la ecuación de la cónica, se obtiene la recta tangente en el punto $ P(x_0, y_0) $:

$$ a_{11}x_0 x + a_{22}y_0 y + a_{12}(x y_0 + x_0 y) + a_{01}(x + x_0) + a_{02}(y + y_0) + a_{00} = 0 $$

Nota. Memorizar esta fórmula puede resultar complicado. Un recurso útil consiste en partir de la ecuación de la cónica y aplicar directamente las sustituciones formales: $$ x^2 \rightarrow x_0 x, \quad y^2 \rightarrow y_0 y, \quad xy \rightarrow \frac{1}{2}(x y_0 + x_0 y) $$ y finalmente, $$ x \rightarrow \frac{1}{2}(x + x_0), \quad y \rightarrow \frac{1}{2}(y + y_0) $$ donde $ x_0 $ y $ y_0 $ son las coordenadas del punto de tangencia. Este método sirve como regla mnemotécnica para recordar fácilmente la fórmula.

Ejemplo práctico

Veamos un ejemplo concreto donde aplicamos esta fórmula para hallar la ecuación de la recta tangente a una cónica.

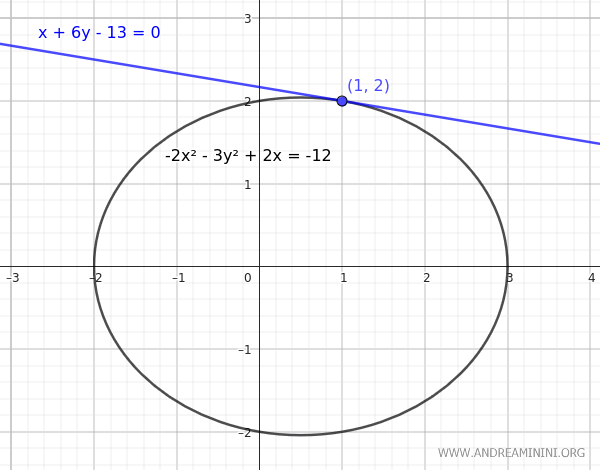
Consideremos la siguiente elipse:

$$ -2x^2 - 3y^2 + 2x = -12 $$

La reescribimos en su forma general:

$$ -2x^2 - 3y^2 + 2x + 12 = 0 $$

Queremos determinar la recta tangente a esta cónica en el punto $ P(1, 2) $.

Aplicamos las sustituciones formales:

$$ x^2 \rightarrow x_0 x, \quad y^2 \rightarrow y_0 y $$

Obtenemos:

$$ -2x_0 x - 3y_0 y + 2x + 12 = 0 $$

Ahora sustituimos $ x \rightarrow \frac{1}{2}(x + x_0) $:

$$ -2x_0 x - 3y_0 y + (x + x_0) + 12 = 0 $$

Con $ x_0 = 1 $ y $ y_0 = 2 $:

$$ -2 \cdot 1 \cdot x - 3 \cdot 2 \cdot y + x + 1 + 12 = 0 $$

$$ -x - 6y + 13 = 0 $$

Multiplicamos por $-1$ para simplificar:

$$ x + 6y - 13 = 0 $$

Ésta es la ecuación de la recta tangente a la elipse en el punto $ P(1, 2) $.

an example of the tangent line at the point (1,2) of the conic section

Método alternativo

También podemos hallar la recta tangente aplicando directamente la fórmula general con los coeficientes identificados:

$$ -2x^2 - 3y^2 + 2x + 12 = 0 $$

Comparando con la forma general:

$ a_{11}x^2 + a_{22}y^2 + 2a_{12}xy + 2a_{01}x + 2a_{02}y + a_{00} = 0 $

Identificamos:

$ a_{11} = -2 $
$ a_{22} = -3 $
$ a_{12} = 0 $
$ a_{01} = 1 $
$ a_{02} = 0 $
$ a_{00} = 12 $

Aplicamos la fórmula:

$$ -2x_0 x - 3y_0 y + (x + x_0) + 12 = 0 $$

Con $ x_0 = 1 $, $ y_0 = 2 $:

$$ -2 \cdot 1 \cdot x - 3 \cdot 2 \cdot y + x + 1 + 12 = 0 $$

$$ -x - 6y + 13 = 0 $$

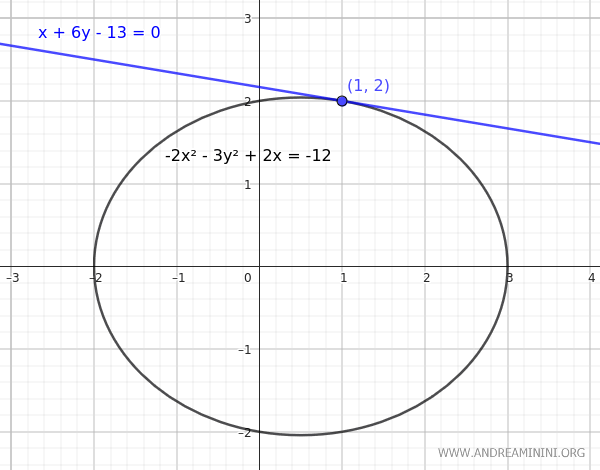
$$ x + 6y - 13 = 0 $$

Hemos obtenido nuevamente la ecuación de la recta tangente deseada en $ P(1, 2) $.

an example of the tangent line at the point (1,2) of the conic section

Así concluye el procedimiento.