Elipse
Una elipse es una figura plana definida como el conjunto de puntos cuya suma de distancias a dos puntos fijos, F1 y F2, llamados focos, permanece constante y es mayor que la distancia entre dichos focos.
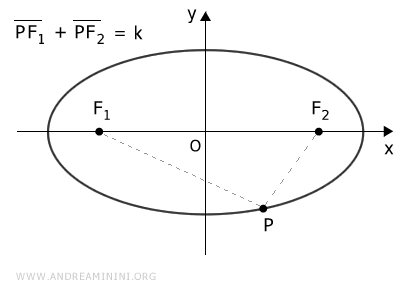
En una elipse con focos F1 y F2, para cualquier punto P sobre la curva, se cumple que la suma PF1 + PF2 es constante.
$$ \overline{PF_1} + \overline{PF_1} = 2a $$
Es decir, si tomamos un punto P cualquiera de la elipse y sumamos sus distancias a los dos focos, el resultado será siempre el mismo: k = 2a.
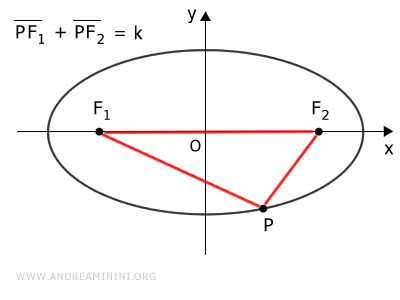
La distancia focal $ \overline{F_1F_2} $ representa la separación entre los dos focos, y siempre es menor que la suma de las distancias PF1 + PF2.
$$ \overline{PF_1} + \overline{PF_2} > \overline{F_1F_2} $$
Nota. Esto se debe al teorema de la desigualdad triangular, que establece que la suma de dos lados de un triángulo siempre es mayor que el tercero. Por tanto, el segmento F1F2 es menor que la suma PF1 + PF2.
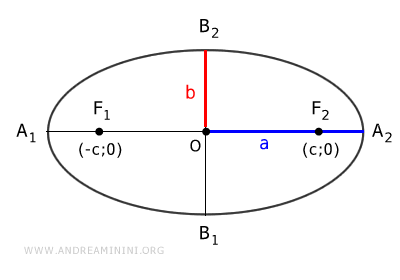
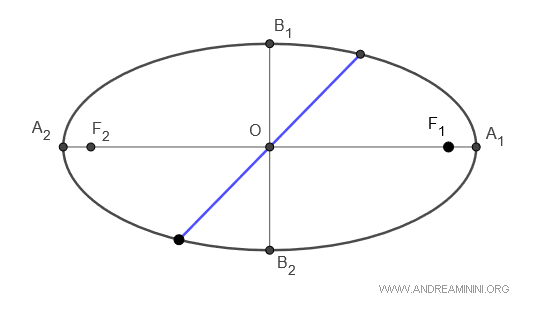
Los ejes de una elipse son dos rectas perpendiculares, A1A2 y B1B2, que se cruzan en el centro (O) de la figura, y se denominan respectivamente eje mayor y eje menor.
- El eje mayor pasa por los focos y corresponde al diámetro más largo.
- El eje menor es perpendicular al eje mayor y representa el diámetro más corto.
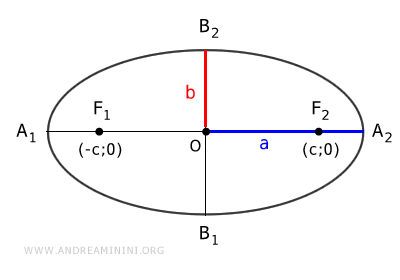
Así, la distancia focal es $ \overline{F_1F_2} = 2c $, la longitud del eje mayor es $ \overline{A_1A_2} = 2a $ y la del eje menor $ \overline{B_1B_2} = 2b $.
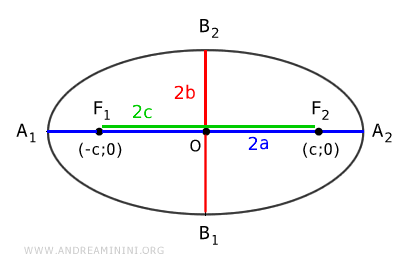
El punto medio del eje mayor se denomina centro de la elipse.
Cuando ambos ejes son iguales (a = b), la elipse se convierte en un círculo.
Los puntos A1, A2, B1 y B2 reciben el nombre de vértices de la elipse.
Desde el punto de vista geométrico, una elipse es una sección cónica, ya que se obtiene al cortar un cono con un plano oblicuo que forma un ángulo comprendido entre θ y π/2 con respecto al eje del cono.
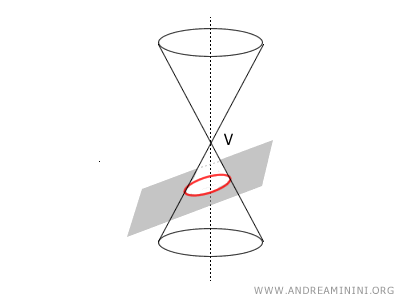
La ecuación de la elipse
La ecuación estándar, conocida como ecuación canónica (o normal) de la elipse, se utiliza cuando la elipse está centrada en el origen del sistema cartesiano:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Aquí, "a" representa la semilongitud del eje mayor y "b" la del eje menor, mientras que x e y son las coordenadas de un punto cualquiera P sobre la elipse.
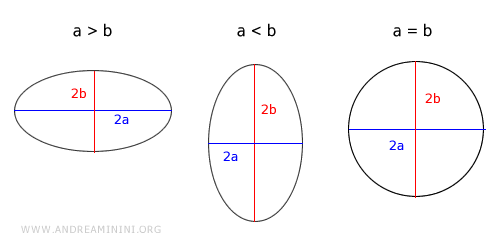
- Si a > b, la elipse se extiende horizontalmente (eje x).
- Si a < b, se extiende verticalmente (eje y).
- Si a = b, la elipse es un círculo.
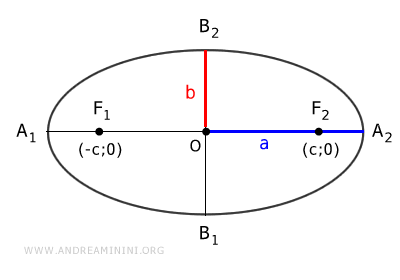
Las coordenadas de los focos dependen de la relación entre los semiejes "a" y "b":
- Si a > b: $$ F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) $$ $$ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) $$
- Si a < b: $$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$
Donde "a" y "b" son las longitudes de los semiejes de la elipse.
Los vértices de la elipse se encuentran en las siguientes coordenadas:
$$ A_1 ( -a; 0) $$
$$ A_2 ( a; 0) $$
$$ B_1 ( 0; -b) $$
$$ B_2 ( 0; b) $$
Estos son los puntos en los que la elipse corta los ejes coordenados.
El grado de alargamiento de la elipse se conoce como excentricidad (e), y se calcula mediante:
- Si a > b: $$ e = \frac{c}{a} $$
- Si a < b: $$ e = \frac{c}{b} $$
- Si a = b, ambas fórmulas son válidas
Donde "a" es el semieje mayor (la mitad de 2a), "b" el semieje menor (la mitad de 2b) y "c" la distancia desde el centro hasta uno de los focos.
El valor de "c" se obtiene aplicando el teorema de Pitágoras:
$$ c = \sqrt{a^2 -b^2} $$
Como c es siempre menor que a y b, se deduce que la excentricidad es un número entre 0 y 1:
$$ 0 \le e < 1 $$
Cuanto más se aproxime e a 1, más alargada será la elipse.
En cambio, cuanto más se acerque e a 0, más se parecerá la elipse a un círculo. Si e = 0, se trata de un círculo.
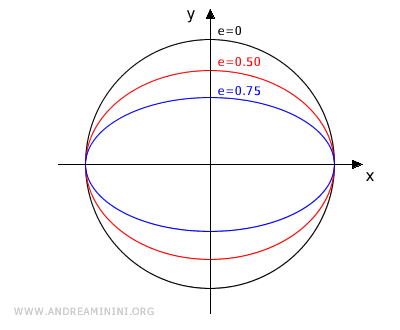
En resumen, la excentricidad mide cuán “circular” es una elipse, y varía entre 0 (círculo) y 1 (elipses muy alargadas).
Nota. Por ello, puede considerarse al círculo como un caso particular de elipse en el que ambos focos coinciden con su centro.
Toda elipse posee dos focos y dos directrices, que son simétricas y perpendiculares al eje focal.
Si el eje focal coincide con el eje x, las ecuaciones de las directrices son:
$$ x = \pm \frac{a^2}{c} $$
Si el eje focal es el eje y, las ecuaciones de las directrices son:
$$ y = \pm \frac{b^2}{c} $$
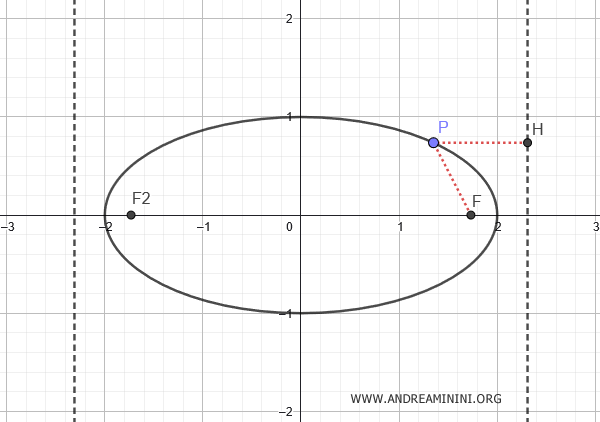
En general, como en toda sección cónica, para cualquier punto $ P(x;y) $ sobre la elipse, la razón entre su distancia a un foco $ \overline{PF} $ y su distancia a una directriz $ \overline{PH} $ es constante, y coincide con la excentricidad.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Un ejemplo práctico
Construyamos una elipse cuyos semiejes horizontal y vertical sean a = 2 y b = 1, respectivamente.
Para facilitar los cálculos, supondremos que el centro de la elipse coincide con el origen del sistema de coordenadas cartesianas: O(0;0).
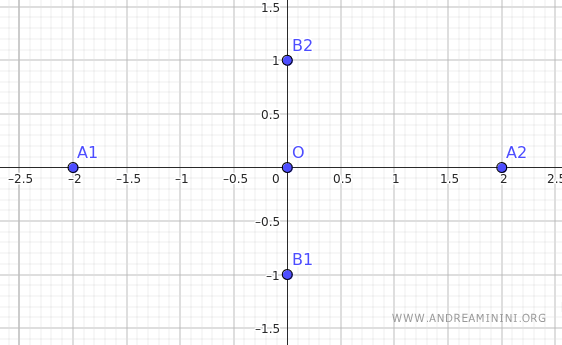
Dado que a = 2 y b = 1, los vértices de la elipse son A1(-2;0), A2(2;0), B1(0;-1) y B2(0;1).
Para determinar las coordenadas de los focos, utilizamos las siguientes expresiones:
$$ \begin{cases} F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) \\ \\ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) \end{cases} $$
Sustituimos los valores de los semiejes a = 2 y b = 1:
$$ \begin{cases} F_1 ( - \sqrt{ 2^2 - 1^2 } ;0 ) \\ \\ F_2 ( \sqrt{ 2^2 - 1^2 } ;0 ) \end{cases} $$
$$ \begin{cases} F_1 ( - \sqrt{ 4 - 1 } ;0 ) \\ \\ F_2 ( \sqrt{ 4 - 1 } ;0 ) \end{cases} $$
$$ \begin{cases} F_1 ( - \sqrt{ 3 } ;0 ) \\ \\ F_2 ( \sqrt{ 3 } ;0 ) \end{cases} $$
Así, la distancia desde el centro de la elipse hasta cada foco es c = √3.
Por tanto, los focos se encuentran en las coordenadas F1(-√3;0) y F2(√3;0).
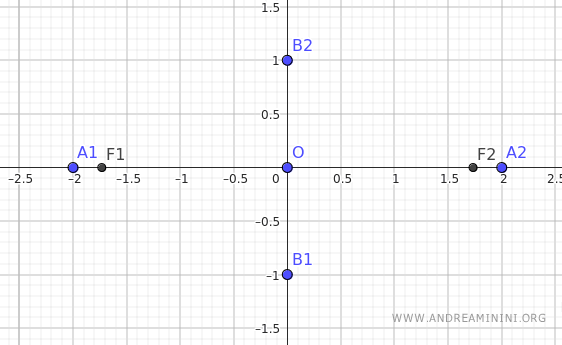
Conocido el valor de "c", podemos calcular la excentricidad de la elipse.
Dado que a > b, utilizamos la fórmula correspondiente:
$$ e = \frac{c}{a} = \frac{ \sqrt{3} }{2} ≈ 0.86 $$
A continuación, aplicamos la ecuación canónica de la elipse para obtener distintos puntos de la curva.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} + \frac{y^2}{1^2} = 1 $$
$$ \frac{x^2}{4} + y^2 = 1 $$
Despejando y:
$$ y^2 = 1 - \frac{x^2}{4} $$
Y extrayendo la raíz cuadrada en ambos miembros:
$$ \sqrt{y^2} = \sqrt{ 1 - \frac{x^2}{4} } $$
$$ y = \pm \sqrt{ 1 - \frac{x^2}{4} } $$
Esta expresión nos permite calcular la coordenada y de cualquier punto cuya abscisa x pertenezca al intervalo [ - a, a], es decir, [ - 2, 2].
| x | y |
|---|---|
| -2 | 0 |
| -1 | ±0.86 |
| 0 | ±1 |
| 1 | ±0.86 |
| 2 | 0 |
Estos son algunos de los puntos que se pueden calcular a partir de la ecuación.
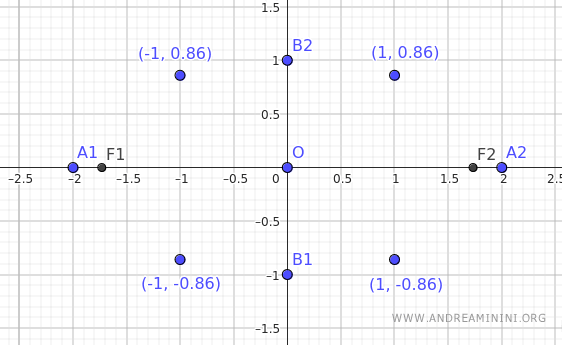
Aunque hemos obtenido pocos valores, ya es posible visualizar la forma general de la elipse.
Repitiendo el procedimiento para otros valores de x, se pueden obtener más puntos y completar la representación gráfica.
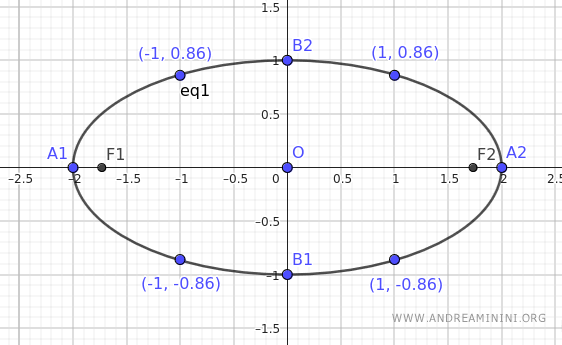
Nota. En este ejemplo he utilizado GeoGebra para construir la elipse. Se trata de una excelente herramienta interactiva que permite explorar visualmente las propiedades de la elipse y experimentar con distintos valores de los semiejes.
Demostración
Las elipses más simples son aquellas cuyo centro O coincide con el origen del sistema de coordenadas cartesianas y cuyos focos se ubican sobre uno de los ejes: el eje x o el eje y.
A] Elipse con focos sobre el eje x
En este caso, los focos se ubican sobre el eje x y el eje mayor coincide con el eje horizontal, lo cual implica que a > b.
$$ a > b $$
Supongamos que los focos se encuentran en los puntos F1(-c, 0) y F2(c, 0), ambos simétricos respecto al centro de la elipse.

La distancia entre los dos focos es igual a 2c:
$$ \overline{F_1F_2} = 2c $$
Por definición, una elipse es el conjunto de puntos cuya suma de distancias a los dos focos permanece constante:
$$ \overline{PF_1} + \overline{PF_2} = k $$
¿Cuál es el valor de la constante k?
Para determinarlo, consideremos el punto A2, situado sobre el eje mayor.
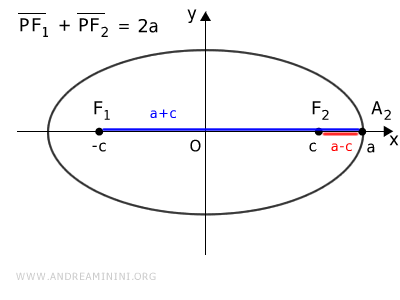
Las distancias desde A2 hasta los focos son:
$$ \overline{A_2F_1} = a + c \quad \text{y} \quad \overline{A_2F_2} = a - c $$
Sumando ambas expresiones, se obtiene:
$$ \overline{A_2F_1} + \overline{A_2F_2} = (a + c) + (a - c) = 2a $$
Por lo tanto, la constante k es igual a 2a. Esto significa que la suma de las distancias desde cualquier punto de la elipse a los dos focos es siempre igual a 2a:
$$ \overline{PF_1} + \overline{PF_2} = 2a $$
¿Cómo se determinan las coordenadas de los focos?
Consideremos ahora el vértice B2, ubicado sobre el eje menor, sabiendo que \( k = 2a \).
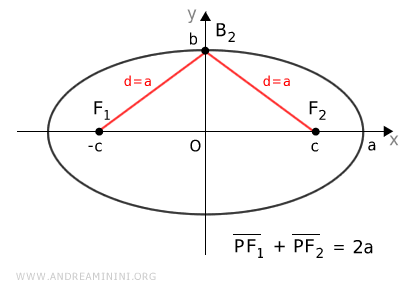
Dado que B2 se encuentra sobre un eje de simetría, las distancias a ambos focos son iguales:
$$ \overline{B_2F_1} = \overline{B_2F_2} = a $$
Esto indica que cada distancia equivale a la mitad del eje mayor, es decir, \( d = a \).
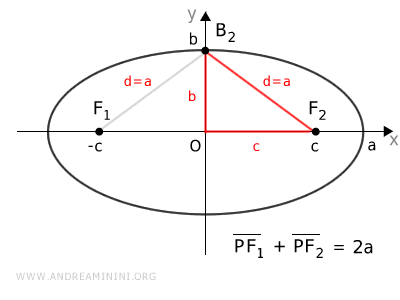
Para hallar el valor de c, aplicamos el Teorema de Pitágoras al triángulo rectángulo OB2F2, donde la hipotenusa es a y los catetos miden b y c:
$$ a^2 = b^2 + c^2 $$
Despejando c:
$$ c^2 = a^2 - b^2 \quad \Rightarrow \quad c = \sqrt{a^2 - b^2} $$
Así, las coordenadas de los focos son:
$$ F_1(-\sqrt{a^2 - b^2}, 0) \quad \text{y} \quad F_2(\sqrt{a^2 - b^2}, 0) $$
¿Cómo se obtiene la ecuación de la elipse?
Consideremos un punto arbitrario \( P(x, y) \) que pertenece a la elipse:
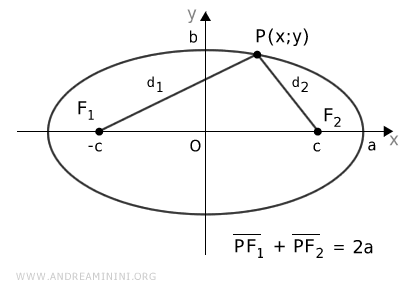
Aplicando el teorema de Pitágoras, podemos calcular las distancias desde el punto P hasta los focos F1 y F2 de la elipse:
$$ d_1 = \sqrt{(x+c)^2 + y^2} $$
$$ d_2 = \sqrt{(x-c)^2 + y^2} $$
Sabemos que, para cualquier punto P sobre la elipse, la suma de dichas distancias es constante e igual a 2a:
$$ d_1 + d_2 = 2a $$
$$ \sqrt{(x+c)^2 + y^2} + \sqrt{(x-c)^2 + y^2} = 2a $$
Si desarrollamos esta expresión algebraicamente, utilizando la identidad \( c^2 = a^2 - b^2 \), y partimos de la relación \( d_1 + d_2 = 2a \), tras una serie de pasos llegamos a la ecuación canónica de la elipse.
Despejamos una de las raíces y la llevamos al segundo miembro:
$$ \sqrt{(x+c)^2 + y^2} = 2a - \sqrt{(x-c)^2 + y^2} $$
Elevamos al cuadrado ambos lados:
$$ \left( \sqrt{(x+c)^2 + y^2} \right)^2 = \left( 2a - \sqrt{(x-c)^2 + y^2} \right)^2 $$
$$ (x+c)^2 + y^2 = 4a^2 - 4a \cdot \sqrt{(x-c)^2 + y^2} + (x-c)^2 + y^2 $$
Expandimos ambos binomios:
$$ x^2 + 2xc + c^2 + y^2 = 4a^2 - 4a \cdot \sqrt{(x-c)^2 + y^2} + x^2 - 2xc + c^2 + y^2 $$
Reducimos términos semejantes:
$$ 2xc = 4a^2 - 4a \cdot \sqrt{(x-c)^2 + y^2} - 2xc $$
$$ 4xc - 4a^2 = -4a \cdot \sqrt{(x-c)^2 + y^2} $$
Volvemos a elevar al cuadrado para eliminar la raíz:
$$ \left(4xc - 4a^2\right)^2 = \left(-4a \cdot \sqrt{(x-c)^2 + y^2} \right)^2 $$
$$ 16x^2c^2 + 16a^4 - 32a^2xc = 16a^2 \cdot \left( (x-c)^2 + y^2 \right) $$
Dividimos todos los términos entre 16:
$$ x^2c^2 + a^4 - 2a^2xc = a^2 \cdot \left( (x-c)^2 + y^2 \right) $$
Dividimos ahora ambos lados entre \( a^2 \):
$$ \frac{x^2c^2}{a^2} + a^2 - 2xc = (x-c)^2 + y^2 $$
Expandimos el cuadrado del binomio en el segundo miembro:
$$ \frac{x^2c^2}{a^2} + a^2 - 2xc = x^2 + c^2 - 2xc + y^2 $$
Reagrupamos y simplificamos:
$$ \frac{x^2c^2}{a^2} + a^2 = x^2 + c^2 + y^2 $$
Llevamos todos los términos conocidos al segundo miembro:
$$ \frac{x^2c^2}{a^2} - x^2 - y^2 = c^2 - a^2 $$
Factorizamos \( x^2 \):
$$ x^2 \left( \frac{c^2}{a^2} - 1 \right) - y^2 = c^2 - a^2 $$
$$ x^2 \cdot \left( \frac{c^2 - a^2}{a^2} \right) - y^2 = c^2 - a^2 $$
Como sabemos que \( c^2 = a^2 - b^2 \), sustituimos:
$$ x^2 \cdot \frac{-b^2}{a^2} - y^2 = -b^2 $$
Multiplicamos ambos lados por -1:
$$ \frac{x^2b^2}{a^2} + y^2 = b^2 $$
Dividimos entre \( b^2 \):
$$ \frac{1}{b^2} \cdot \left( \frac{x^2b^2}{a^2} + y^2 \right) = \frac{1}{b^2} \cdot b^2 $$
$$ \frac{x^2b^2}{a^2b^2} + \frac{y^2}{b^2} = 1 $$
Finalmente, simplificamos:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Este es el resultado final: la ecuación canónica de la elipse, donde x e y son las coordenadas de un punto genérico P sobre la curva, y a y b representan las longitudes de los semiejes mayor y menor, respectivamente.
Desarrollo alternativo de la demostración. Partimos de la ecuación:
$$ 4xc - 4a^2 = - 4a \cdot \sqrt{(x-c)^2 + y^2} $$
Dividimos ambos miembros entre cuatro:
$$ xc - a^2 = - a \cdot \sqrt{(x-c)^2 + y^2} $$
Multiplicamos ambos lados por -1:
$$ a^2 - xc = a \cdot \sqrt{(x-c)^2 + y^2} $$
Elevamos ambos miembros al cuadrado:
$$ (a^2 - xc)^2 = \left( a \cdot \sqrt{(x-c)^2 + y^2} \right)^2 $$
$$ (a^2 - xc)^2 = a^2 \cdot \left[ (x-c)^2 + y^2 \right] $$
Desarrollamos ambos lados:
$$ a^4 - 2a^2xc + x^2c^2 = a^2(x^2 - 2xc + c^2 + y^2) $$
$$ \require{cancel} a^4 - \cancel{2a^2xc} + x^2c^2 = a^2x^2 - \cancel{2a^2xc} + a^2c^2 + a^2y^2 $$
Simplificamos:
$$ a^4 - a^2c^2 = a^2x^2 - x^2c^2 + a^2y^2 $$
Factorizamos en ambos lados:
$$ a^2(a^2 - c^2) = x^2(a^2 - c^2) + a^2y^2 $$
Como \( a^2 - c^2 = b^2 \), sustituimos:
$$ a^2b^2 = b^2x^2 + a^2y^2 $$
Dividimos ambos lados entre \( a^2b^2 \):
$$ \frac{a^2b^2}{a^2b^2} = \frac{b^2x^2 + a^2y^2}{a^2b^2} $$
$$ 1 = \frac{b^2x^2}{a^2b^2} + \frac{a^2y^2}{a^2b^2} $$
$$ 1 = \frac{x^2}{a^2} + \frac{y^2}{b^2} $$
Esta es la ecuación canónica (o estándar) de la elipse, que era el objetivo de esta demostración:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
B] Elipse con focos sobre el eje y
Ahora consideramos el caso en que los focos se encuentran sobre el eje y, lo cual implica que el eje mayor es vertical:
$$ b > a $$
Los focos se sitúan en F1(0, - c) y F2(0, c), simétricos respecto al centro.
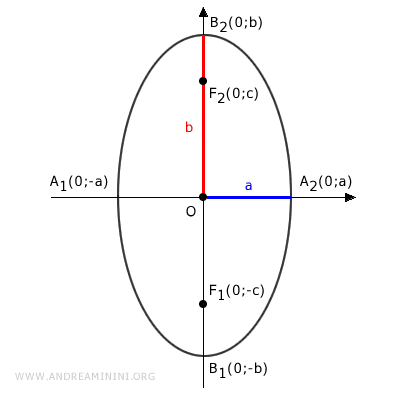
La longitud del eje mayor es 2b, por lo que la suma de distancias desde cualquier punto P cumple:
$$ \overline{PF_1} + \overline{PF_2} = 2b $$
La demostración es análoga a la anterior.
Si consideramos el vértice B2, se tiene:
$$ \overline{B_2F_1} = b + c \quad\quad \overline{B_2F_2} = b - c $$
Por tanto:
$$ \overline{B_2F_1} + \overline{B_2F_2} = 2b $$
Con lo cual se confirma que la suma es constante e igual a 2b en toda la elipse.
Como b > a, los focos de esta elipse están sobre el eje y:
$$ F_1 (0; - \sqrt{ b^2 - a^2 }) \quad\quad F_2 (0; \sqrt{ b^2 - a^2 }) $$
La ecuación canónica sigue siendo:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
y se aplican todas las propiedades vistas en el caso anterior.
Historia de la elipse
La elipse fue estudiada por primera vez por los matemáticos de la antigua Grecia.
En el siglo IV a.C., Menaecmo, discípulo de Eudoxo y contemporáneo de Platón, descubrió las secciones cónicas, entre ellas la elipse, al cortar un cono con un plano inclinado que no es paralelo a la base.

El mayor avance en la teoría de las cónicas lo realizó Apolonio en el siglo III a.C., con su obra en ocho volúmenes titulada Secciones cónicas. En ella sistematizó y amplió los conocimientos previos, introduciendo los términos elipse, parábola e hipérbola. Fue también el primero en deducir todas las secciones cónicas a partir de un único cono, ya que hasta entonces se utilizaban conos distintos para obtener cada curva.
Durante la Edad Media, el legado matemático griego fue preservado y desarrollado por los sabios árabes. La elipse siguió siendo objeto de estudio, y numerosas obras griegas fueron traducidas primero al árabe y más tarde al latín.
En el siglo XVII, la elipse adquirió un papel fundamental en la astronomía: Kepler descubrió que las órbitas de los planetas alrededor del Sol no eran circulares, sino elípticas.
Con el surgimiento de la geometría analítica, René Descartes introdujo el sistema de coordenadas cartesianas, lo que permitió expresar las curvas mediante ecuaciones algebraicas. La ecuación estándar de la elipse, \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \), se deriva precisamente de este enfoque.
Desde entonces, la elipse ha encontrado múltiples aplicaciones en la ciencia y la ingeniería: desde los espejos elípticos hasta el estudio de trayectorias bajo la acción de fuerzas centrales.
Simetría de la elipse
La elipse presenta una simetría doble respecto a sus dos ejes principales: el eje mayor y el eje menor.
Esto significa que, por cada punto sobre la elipse, existe otro que es simétrico respecto a dichos ejes.
Nota. Esta propiedad se debe al hecho de que en su ecuación, las variables x e y están elevadas al cuadrado. El cuadrado de un número es igual al cuadrado de su opuesto, es decir: \( x^2 = (-x)^2 \) y \( y^2 = (-y)^2 \). Por tanto, la elipse es simétrica tanto respecto al eje x como respecto al eje y: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Leftrightarrow \frac{(-x)^2}{a^2} + \frac{y^2}{b^2} = 1 $$ $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Leftrightarrow \frac{x^2}{a^2} + \frac{(-y)^2}{b^2} = 1 $$
Existen tres simetrías características en una elipse:
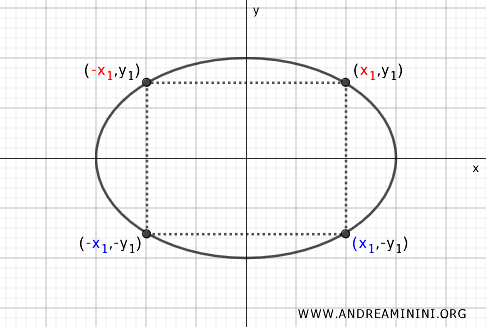
- Simetría respecto al eje y
Dado un punto \( P(x, y) \) sobre la elipse, su simétrico respecto al eje y es \( P'(-x, y) \). Esto implica que la elipse permanece inalterada al reflejarse sobre ese eje.
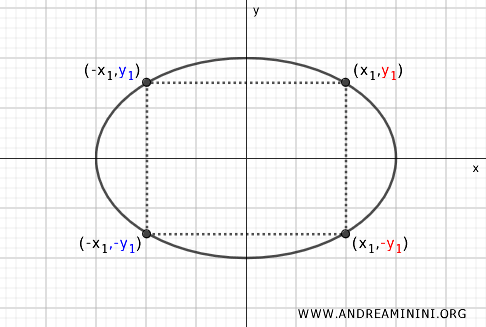
- Simetría respecto al eje x
Análogamente, el simétrico de \( P(x, y) \) respecto al eje x es \( P(x, -y) \), lo que demuestra que la curva conserva su forma si se refleja verticalmente.
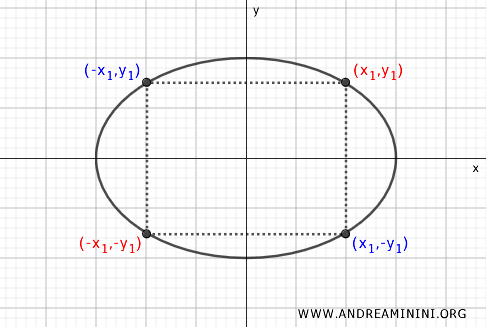
- Simetría respecto al origen
Para cualquier punto \( P(x, y) \), el punto \( P'(-x, -y) \) también pertenece a la elipse. Esto indica simetría central respecto al origen de coordenadas.
Observaciones
Algunas propiedades y hechos relevantes sobre la elipse:
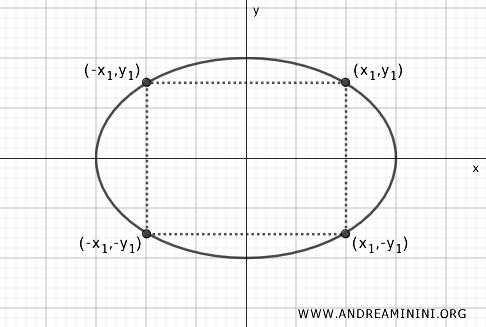
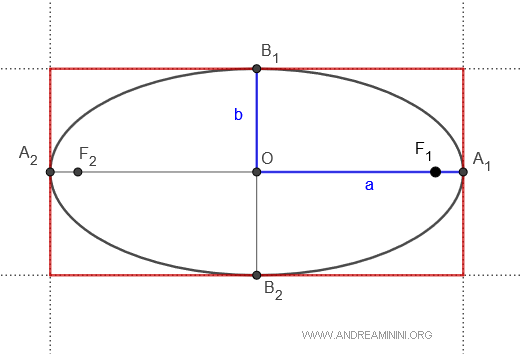
- La elipse está inscrita en un rectángulo
Toda elipse puede inscribirse en un rectángulo cuyos lados miden 2a y 2b, y que pasa por sus vértices.
- La elipse es una cónica
Forma parte de la familia de las secciones cónicas, junto con la parábola, la hipérbola y la circunferencia, y se obtiene al cortar un cono con un plano oblicuo. - Cuando la excentricidad es cero, la elipse es una circunferencia
Si \( e = 0 \), los dos focos coinciden con el centro y la elipse se reduce a una circunferencia. - Diámetros de la elipse
Toda cuerda que pasa por el centro de la elipse recibe el nombre de “diámetro”.
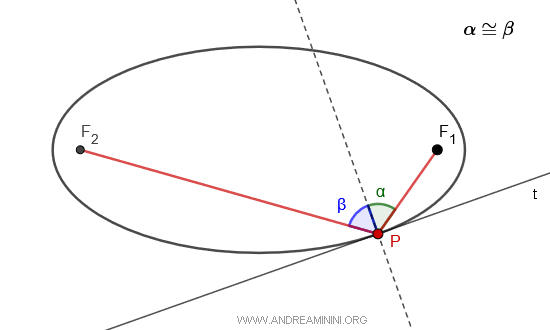
- Propiedad focal
En cualquier punto P de la elipse, la bisectriz del ángulo entre los segmentos PF1 y PF2 es perpendicular a la tangente en P. Es decir, los radios focales \( \overline{PF_1} \) y \( \overline{PF_2} \) forman ángulos congruentes con la normal a la curva en ese punto \( \alpha \cong \beta \).
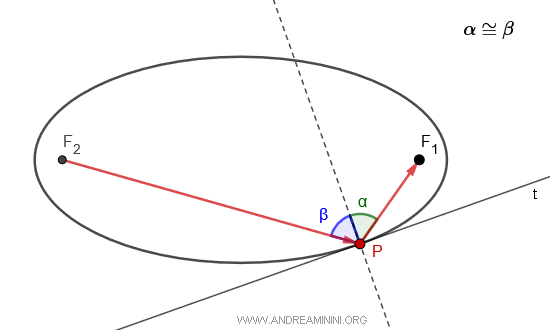
Esta propiedad explica por qué un rayo de luz que parte de un foco y rebota en la elipse siempre se dirige hacia el otro foco.
- La elipse como deformación de una circunferencia
La ecuación de una circunferencia centrada en el origen es: $$ x^2 + y^2 = 1 $$. Si aplicamos una dilatación con factores \( a \) en x y \( b \) en y: $$ \begin{cases} x' = ax \\ y' = by \end{cases} $$ entonces, despejando x e y: $$ \begin{cases} x = \frac{x'}{a} \\ y = \frac{y'}{b} \end{cases} $$ y sustituyendo en la ecuación de la circunferencia: $$ \left( \frac{x'}{a} \right)^2 + \left( \frac{y'}{b} \right)^2 = 1 $$ se obtiene la ecuación de una elipse centrada en el origen: $$ \frac{x'^2}{a^2} + \frac{y'^2}{b^2} = 1 $$
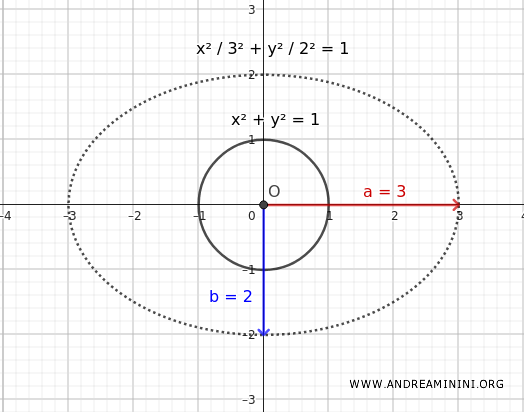
Relación entre áreas. Si la circunferencia de partida tiene radio 1, su área es \( s = \pi \). La elipse obtenida por dilatación tiene un área \( s' \) proporcional al producto de los factores de escala: $$ s' = \pi \cdot ab $$
Y así sucesivamente.