Cómo hallar la ecuación de una elipse conociendo un foco y un semieje
Si una elipse está centrada en el origen \( O(0,0) \) y se conoce uno de sus focos \( F(xf, yf) \) junto con la longitud de uno de sus semiejes, es posible determinar su ecuación utilizando el teorema de Pitágoras.
Ejemplo práctico
Supongamos una elipse con centro en el origen \( O(0,0) \), foco en \( F(4,0) \) y semieje vertical de longitud \( b = 3 \).
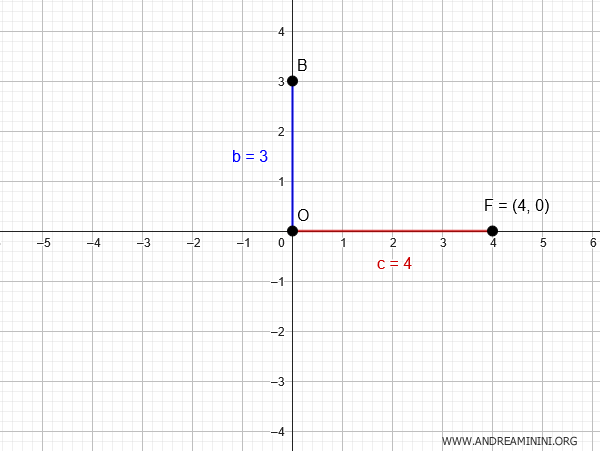
La distancia entre el centro y el foco, denominada distancia focal, es \( c = 4 \).
La ecuación general de una elipse con centro en el origen es:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Ya disponemos del valor del semieje vertical: \( b = 3 \). Para completar la ecuación, necesitamos calcular la longitud del semieje horizontal \( a \).
Dado que los valores de \( a \), \( b \) y \( c \) están relacionados mediante el teorema de Pitágoras, podemos usar la fórmula:
$$ a^2 = b^2 + c^2 $$
Sustituyendo los datos conocidos:
$$ a^2 = 3^2 + 4^2 $$
$$ a^2 = 9 + 16 $$
$$ a^2 = 25 $$
$$ a = 5 $$
Por lo tanto, la longitud del semieje horizontal es \( a = 5 \), y los extremos de dicho eje se encuentran en los puntos \( A(5,0) \) y \( A_2(-5,0) \), simétricos respecto al centro \( O(0,0) \).
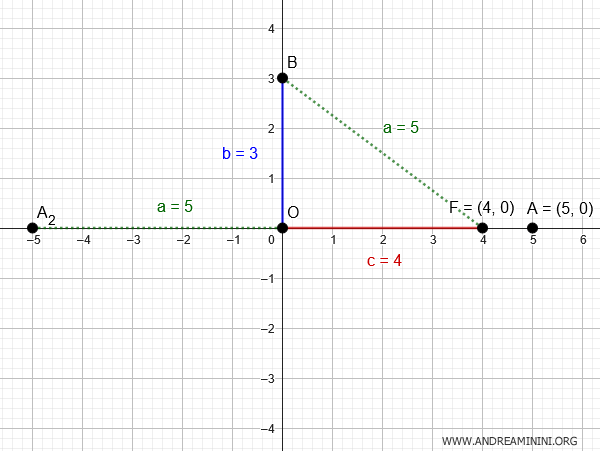
Ahora que conocemos ambos semiejes, \( a = 5 \) y \( b = 3 \), podemos escribir la ecuación completa de la elipse:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{5^2} + \frac{y^2}{3^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
A continuación, se muestra la representación gráfica correspondiente a esta ecuación:
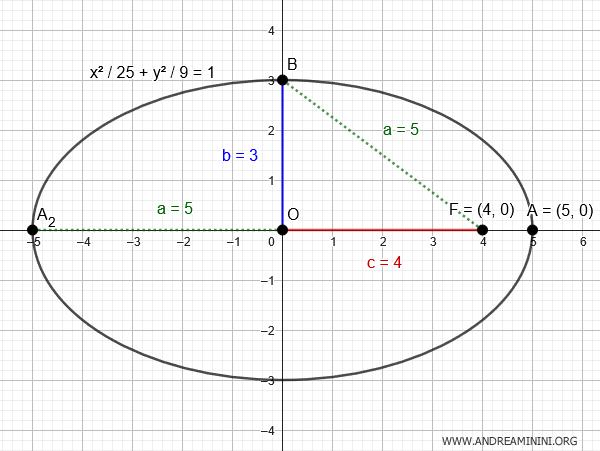
Así es como se obtiene la ecuación de una elipse a partir de un foco y la longitud de un semieje.